Self-Organising Memristive Networks as Physical Learning Systems (2509.00747v1)

Abstract: Learning with physical systems is an emerging paradigm that seeks to harness the intrinsic nonlinear dynamics of physical substrates for learning. The impetus for a paradigm shift in how hardware is used for computational intelligence stems largely from the unsustainability of artificial neural network software implemented on conventional transistor-based hardware. This Perspective highlights one promising approach using physical networks comprised of resistive memory nanoscale components with dynamically reconfigurable, self-organising electrical circuitry. Experimental advances have revealed the non-trivial interactions within these Self-Organising Memristive Networks (SOMNs), offering insights into their collective nonlinear and adaptive dynamics, and how these properties can be harnessed for learning using different hardware implementations. Theoretical approaches, including mean-field theory, graph theory, and concepts from disordered systems, reveal deeper insights into the dynamics of SOMNs, especially during transitions between different conductance states where criticality and other dynamical phase transitions emerge in both experiments and models. Furthermore, parallels between adaptive dynamics in SOMNs and plasticity in biological neuronal networks suggest the potential for realising energy-efficient, brain-like continual learning. SOMNs thus offer a promising route toward embedded edge intelligence, unlocking real-time decision-making for autonomous systems, dynamic sensing, and personalised healthcare, by enabling embedded learning in resource-constrained environments. The overarching aim of this Perspective is to show how the convergence of nanotechnology, statistical physics, complex systems, and self-organising principles offers a unique opportunity to advance a new generation of physical intelligence technologies.

• The paper introduces SOMNs that harness memristive dynamics to achieve adaptive, autonomous learning analogous to biological synaptic plasticity.
• It employs a theoretical framework combining graph theory, Kirchhoff’s laws, and mean-field approximations to model critical conductance transitions.
• The work demonstrates practical application in reservoir computing and associative learning, paving the way for scalable cognitive architectures.

Self-Organising Memristive Networks as Physical Learning Systems

Introduction to Self-Organising Memristive Networks

The emergence of learning paradigms that leverage physical substrates is driven by the inherent limitations of conventional transistor-based hardware in handling complex learning tasks, particularly those analogous to biological processes. Self-Organising Memristive Networks (SOMNs) have come forward as an innovative blueprint in this context, involving dynamic, reconfigurable networks of memristive components that exhibit collective nonlinear dynamics. Such networks are capable of adaptive learning through alterations in their structural and functional properties under external stimuli.

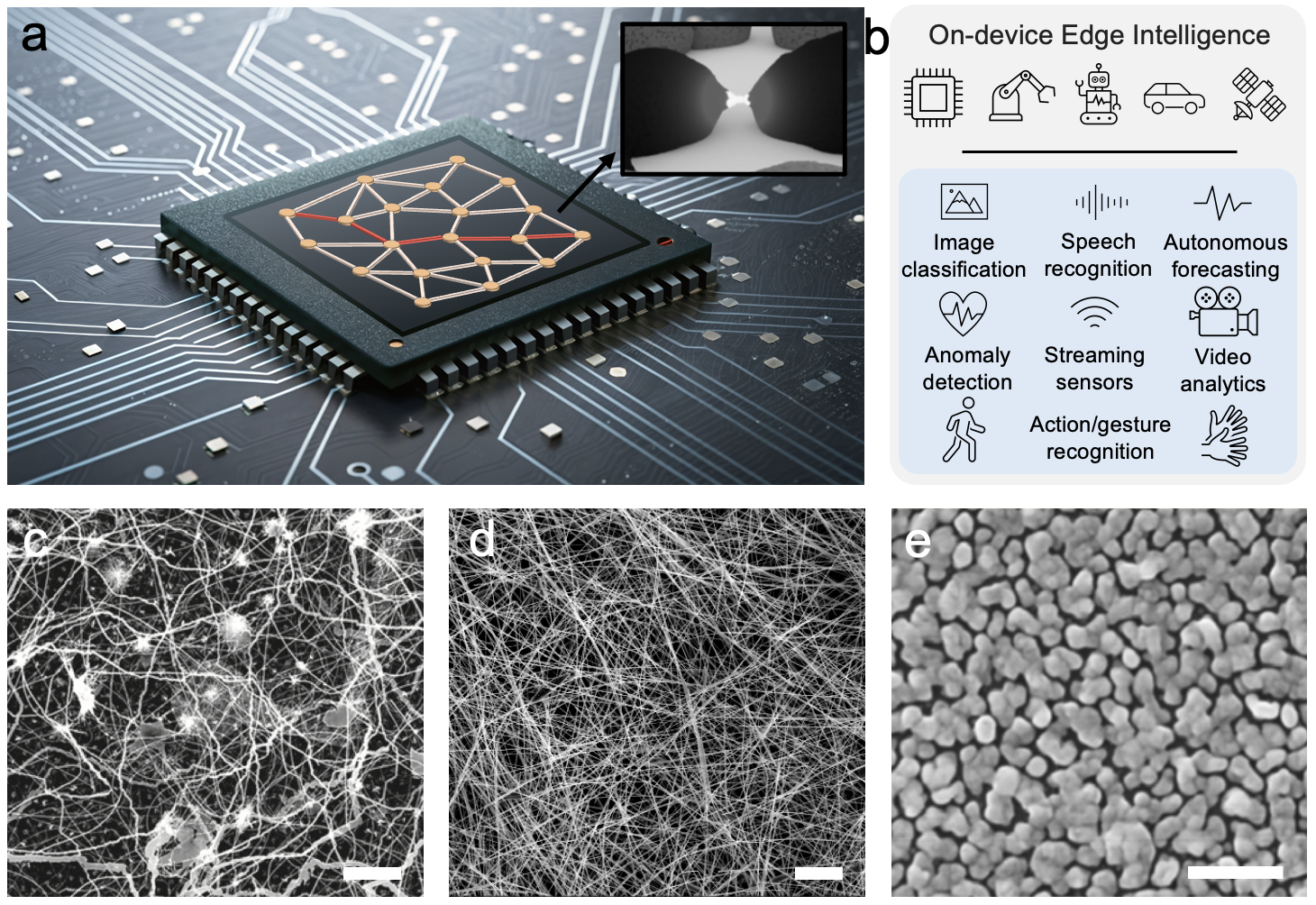
Figure 1: Conceptual overview of self-organised memristive networks (SOMNs) as a platform for physical learning systems.

Memristive Networks in Learning Systems

The distinctive neuromorphic attributes of SOMNs are founded on their intrinsic dynamics and structural complexity. These systems functionally resemble biological neuronal networks by virtue of their plasticity and criticality, mirroring the roles of synaptic plasticity and dynamic adaptation in biological cognition.

Plasticity and Dynamics

SOMNs exhibit both short-term and long-term plasticity through reconfiguration at the synaptic level in response to electrical stimuli—a property made possible by the underlying nanoscale transport dynamics (ionic or atomic rearrangements) of their components.

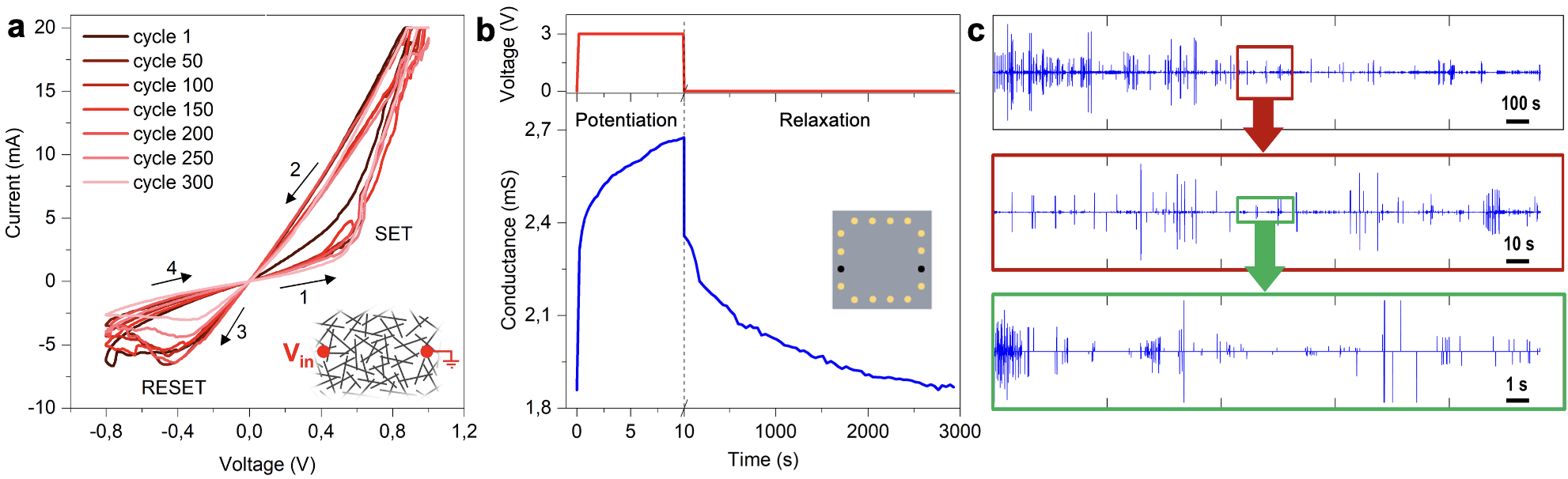
Figure 2: Memristive behaviour of SOMNs.

Nanoscale transport mechanisms in SOMNs give rise to characteristic dynamics that form the basis of their learning capabilities. Ionic dynamics, predominant in nanowire networks, and atomic rearrangements, typical in nanoparticle networks, drive the memory and adaptive features critical for learning.

Collective Criticality

The critical dynamics that emerge from the interplay between network topology and nanoscale transport are analogous to phase transitions in disordered systems. This abrupt transition in conductance states—criticality—enables SOMNs to modulate complex information efficiently.

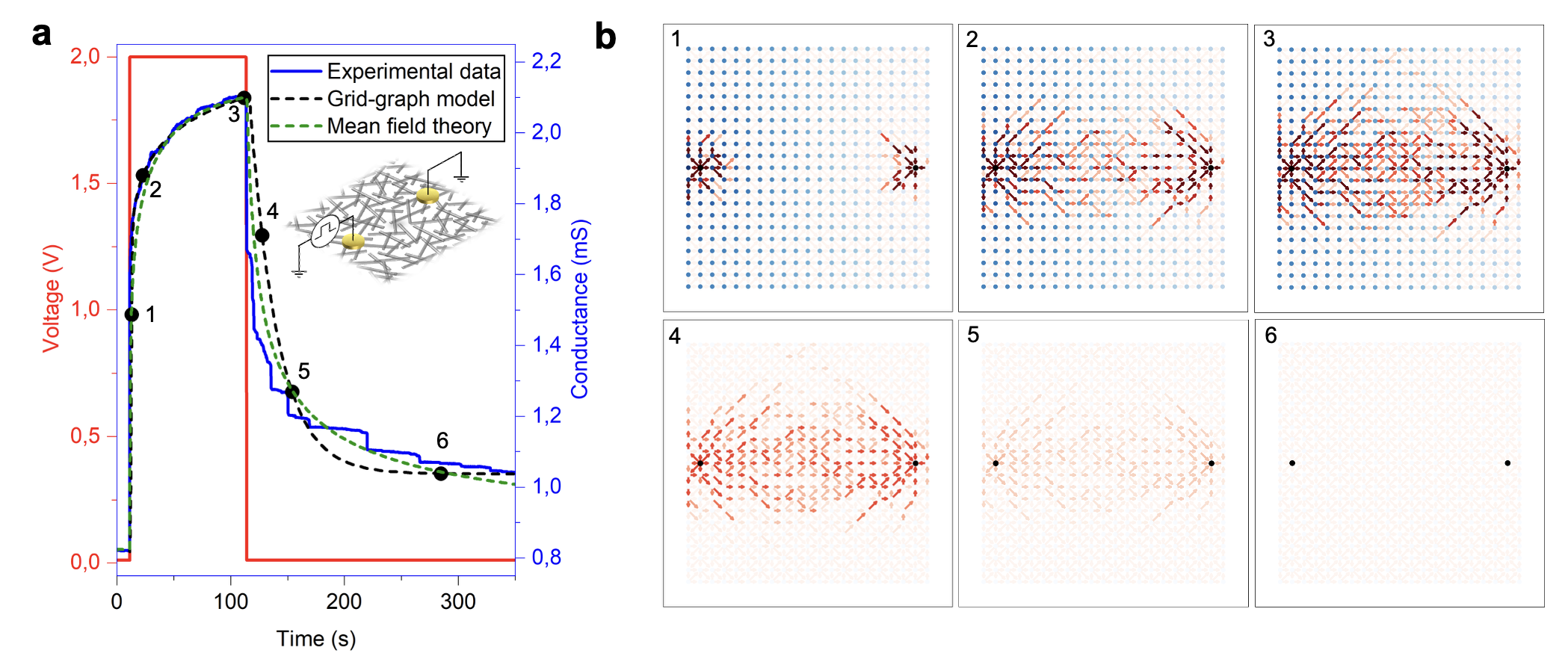
Figure 3: Modeling emergent behaviour of memristive networks.

Theoretical Framework and Modeling

SOMNs are best understood through a robust theoretical framework that combines graph theory with nonlinear dynamics. Kirchhoff’s laws introduce constraints that are analytically described using projector operators, facilitating the exploration of SOMNs' behavior and adaptability.

Mean Field Approximations

The mean-field theoretical approach provides foundational insights into possible conductance transitions within SOMNs. By analyzing these transition dynamics, researchers can determine optimal conditions for learning and adaptation.

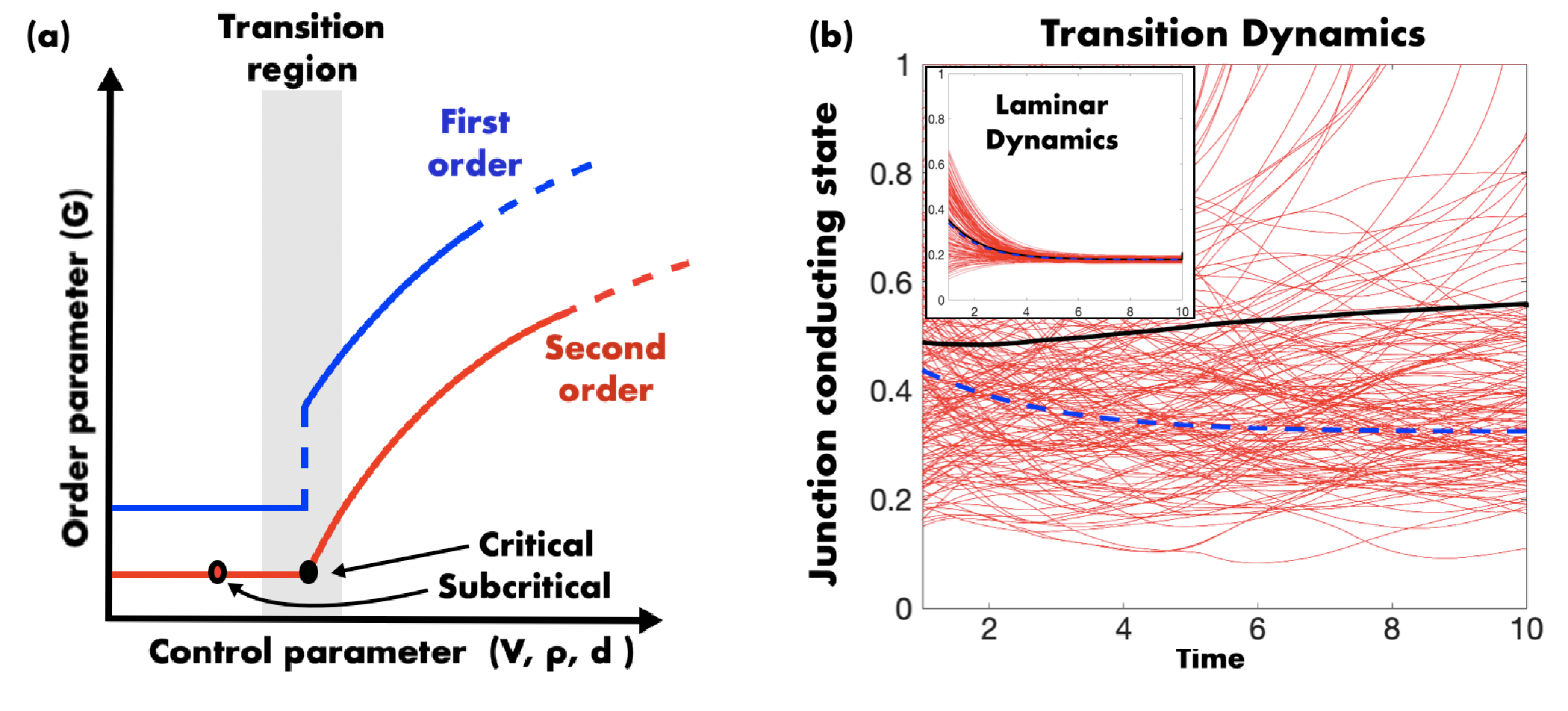
Figure 4: Conductance transitions in memristive networks.

Implementing Learning with SOMNs

Physical Reservoir Computing

Reservoir computing leverages the non-linear dynamics of SOMNs, wherein high-dimensional input mapping onto network states provides a basis for learning. These networks efficiently execute this process with their inherent properties, functioning as computational reservoirs.

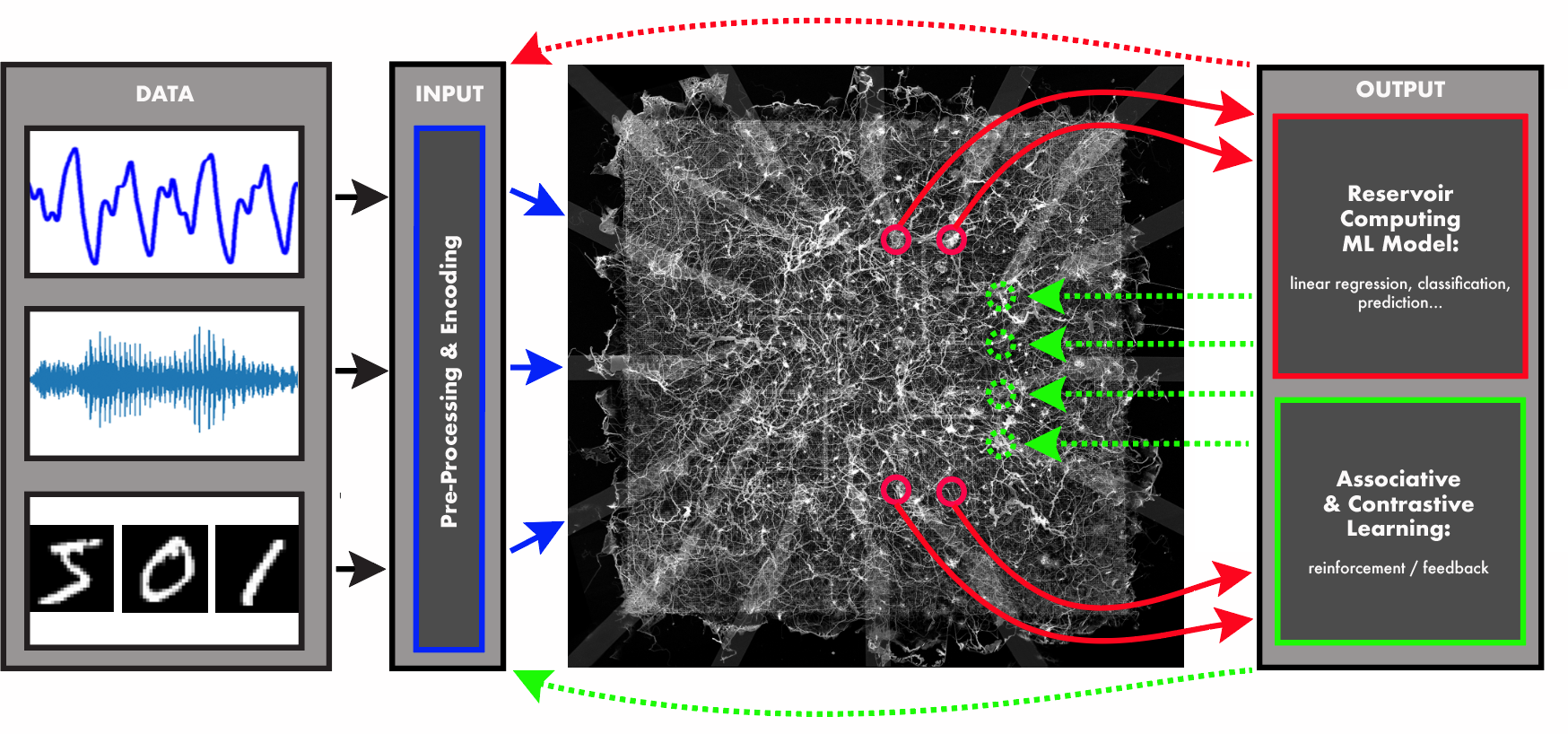
Figure 5: Physical learning paradigms for self-organising memristive networks.

Associative and Contrastive Learning

Associative learning is embedded within the physical structures of SOMNs, wherein these networks intrinsically adapt to recognize and recall input patterns through practice-based feedback. This intrinsic learning mechanism ensures efficient and autonomous cognitive processing.

Conclusion

Self-Organising Memristive Networks position themselves as potent platforms for next-generation artificial learning systems. Through leveraging their intrinsic dynamics and structural adaptability, they offer a promising conduit toward autonomous, efficient, and scalable cognitive architectures. Future advancements will focus on refined control of critical dynamics, broader scope in learning tasks, and optimizing physical implementations for real-world applications.