Finite entropy sums in quantum field theory (2508.21276v1)

Abstract: Entropies associated with spatial subsystems in conventional local quantum field theories are typically divergent when the spatial regions have boundaries. However, in certain linear combinations of the entropies for various subsystems, these divergences may cancel, giving finite quantities that provide information-theoretic data about the underlying state. In this note, we show that all such quantities can be written as linear combinations of three basic types of quantities: i) the entropy of a spatial subsystem minus the entropy of its complementary subsystem, ii) the mutual information between non-adjacent subsystems, and iii) the tripartite information for triples of disjoint sub-systems. For a fixed decomposition of a spatial slice into regions, we describe a basis of sums of entropies for collections of for these regions for which all divergences related to both region boundaries and higher-codimension intersections of regions cancel. Key mathematical technology used in this work (Fourier transforms on the Boolean cube and M\"obius transformations of functions on partially ordered sets) and several of the main proof ideas were suggested by AI (ChatGPT5). We offer a few comments on the use of AI in physics and mathematics, based on our experience.

• The paper provides a rigorous classification of finite entropy sums as all being linear combinations of three basic types that cancel codimension-one divergences.
• It applies graph and hypergraph formulations alongside Fourier and Möbius analysis on the Boolean cube to construct a complete, orthogonal basis.
• The study links the finite entropy framework to algebraic definitions in operator algebras, offering new insights into entanglement in QFT and many-body systems.

Finite Entropy Sums in Quantum Field Theory: A Rigorous Characterization

Introduction and Motivation

Entanglement entropy is a central tool in quantum field theory (QFT) for probing the structure of quantum correlations and the nature of quantum states. However, in local QFTs, the entanglement entropy of a spatial region is typically divergent due to the infinite number of UV degrees of freedom at the boundary of the region. This divergence is a manifestation of the type III property of local operator algebras and is not regularization-independent. Nevertheless, certain linear combinations of entropies—such as mutual information and tripartite information—can be constructed so that the leading divergences cancel, yielding finite, physically meaningful quantities. The paper "Finite entropy sums in quantum field theory" (2508.21276) provides a comprehensive and rigorous mathematical framework for classifying all such finite entropy combinations, using tools from graph theory, Boolean function analysis, and combinatorics.

Divergence Structure and Finite Entropy Combinations

The divergences in entanglement entropy are local and associated with the geometry of the region's boundary. For a spatial slice $\Sigma$ partitioned into $n$ regions $\{A_i\}$, the entropy $S(A_i)$ of each region is divergent, but certain linear combinations can be finite if the divergences cancel. The paper identifies three fundamental types of finite entropy combinations:

1. Entropy difference between a region and its complement: $S(A) - S(A^c)$.
2. Mutual information between non-adjacent regions: $I(A,B) = S(A) + S(B) - S(A \cup B)$.
3. Tripartite information for three disjoint regions: $$I(A,B,C) = S(A) + S(B) + S(C) - S(A \cup B) - S(A \cup C) - S(B \cup C) + S(A \cup B \cup C)$$.

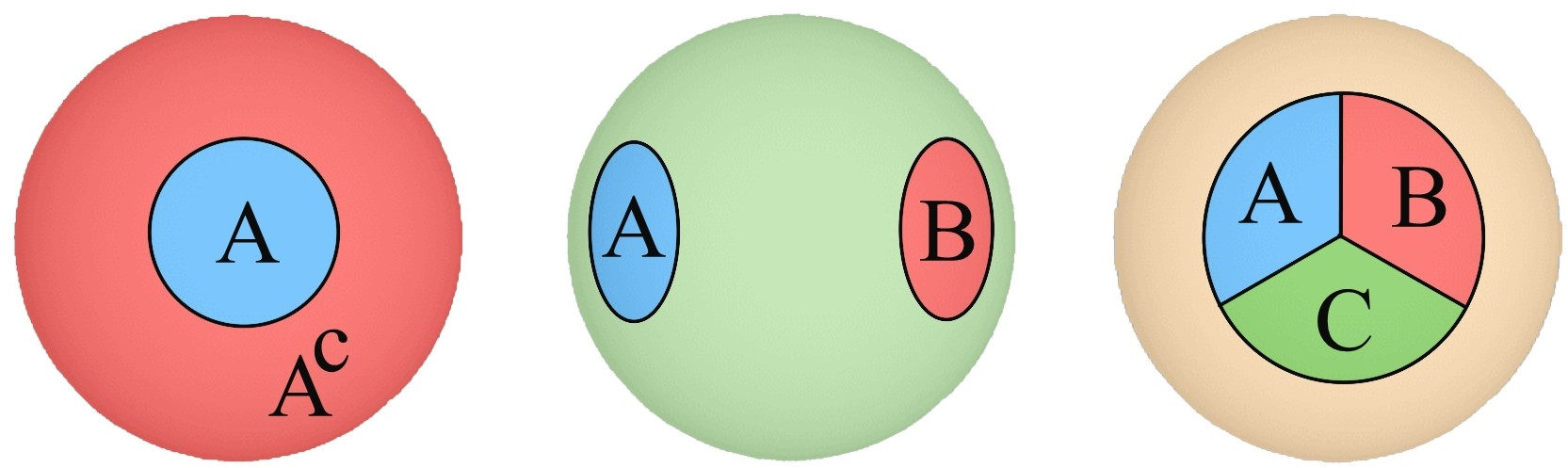
   Figure 1: Example regions for the three basic types of finite entropy combinations: (i) $S(A) - S(A^c)$, (ii) $I(A,B)$, and (iii) $I(A,B,C)$.

The main result is that all finite entropy sums with cancellation of codimension-one (boundary) divergences are linear combinations of these three types. The paper further provides explicit bases for the space of such combinations, taking into account both codimension-one and higher-codimension (corner, edge) divergences.

Graph and Hypergraph Formulation

The adjacency relations among the regions are encoded in a graph $G$ with vertices corresponding to regions and edges indicating shared boundaries. The problem of classifying finite entropy sums is then mapped to the problem of finding functions on the Boolean cube (the set of all subsets of regions) that satisfy certain linear constraints associated with the edges of $G$.

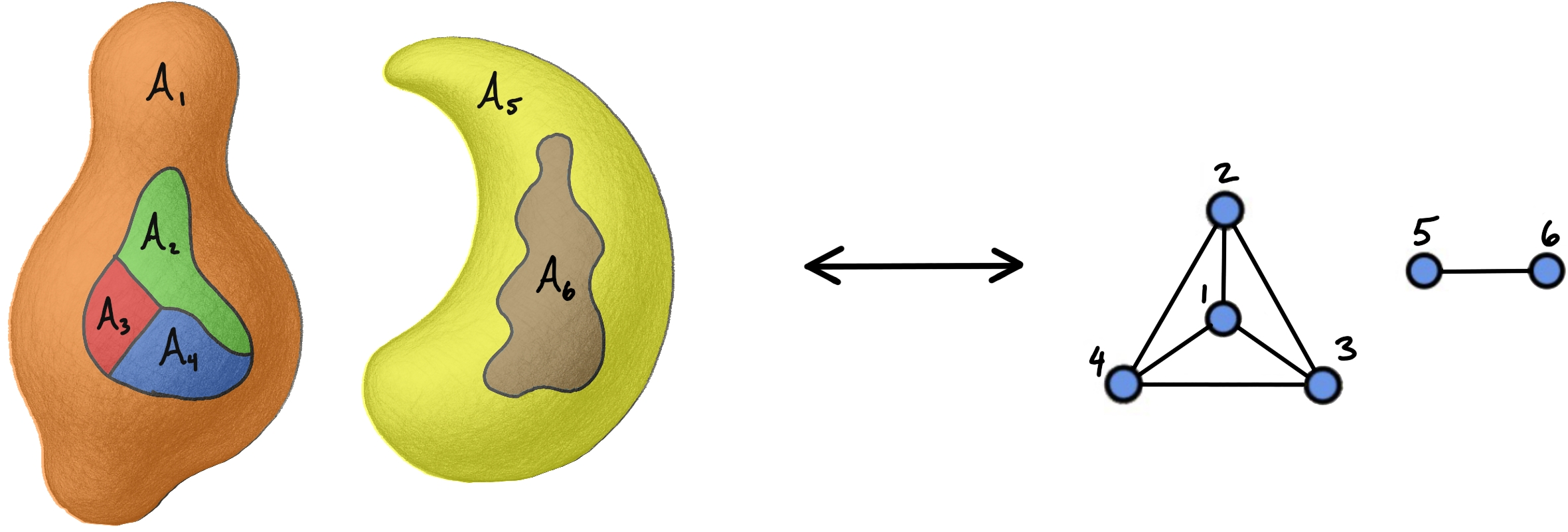
Figure 3: Example of a spatial manifold $\Sigma$ divided into regions $A_i$, with the associated graph $G$ capturing adjacency properties.

The key insight is that the space of finite entropy sums corresponds to the kernel of a linear operator $\mathcal{E}$, which encodes the requirement that the sum of coefficients for all regions sharing a given boundary vanishes. This is formalized as:

$$\sum_{\sigma: B_{ij} \in \partial A_\sigma} c_\sigma = 0 \quad \forall B_{ij}$$

where $B_{ij}$ is a codimension-one boundary between $A_i$ and $A_j$.

Fourier and Möbius Analysis on the Boolean Cube

The paper leverages the Fourier transform on the Boolean cube to construct an explicit orthogonal basis for the space of finite entropy sums. Each function on the Boolean cube can be expanded in the Fourier basis $\{\chi_\sigma\}$, and the divergence cancellation conditions translate into constraints on the Fourier coefficients.

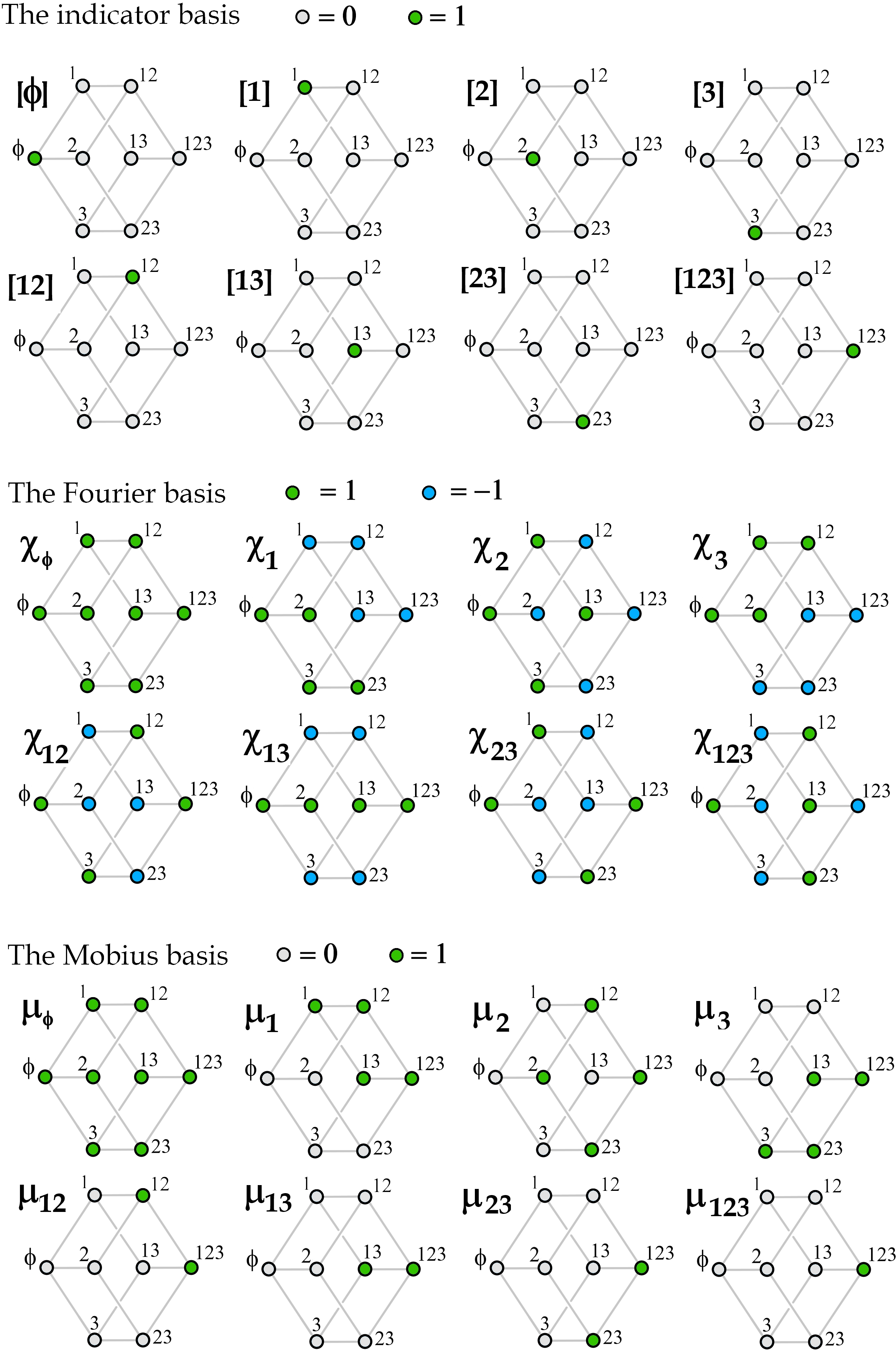
Figure 2: Indicator, Fourier, and Möbius bases for functions on subsets of a three-element set $\{1,2,3\}$.

The main theorem states that the kernel of $\mathcal{E}$ is spanned by all Fourier basis elements except those corresponding to the empty set and to edges of $G$, together with a specific linear combination of these excluded elements. This provides a complete and orthogonal basis for the space of finite entropy sums.

Additionally, the Möbius transform is used to construct an alternative "information-theoretic" basis, consisting of the three types of entropy combinations described above. This basis is more physically transparent and has a direct interpretation in terms of information measures.

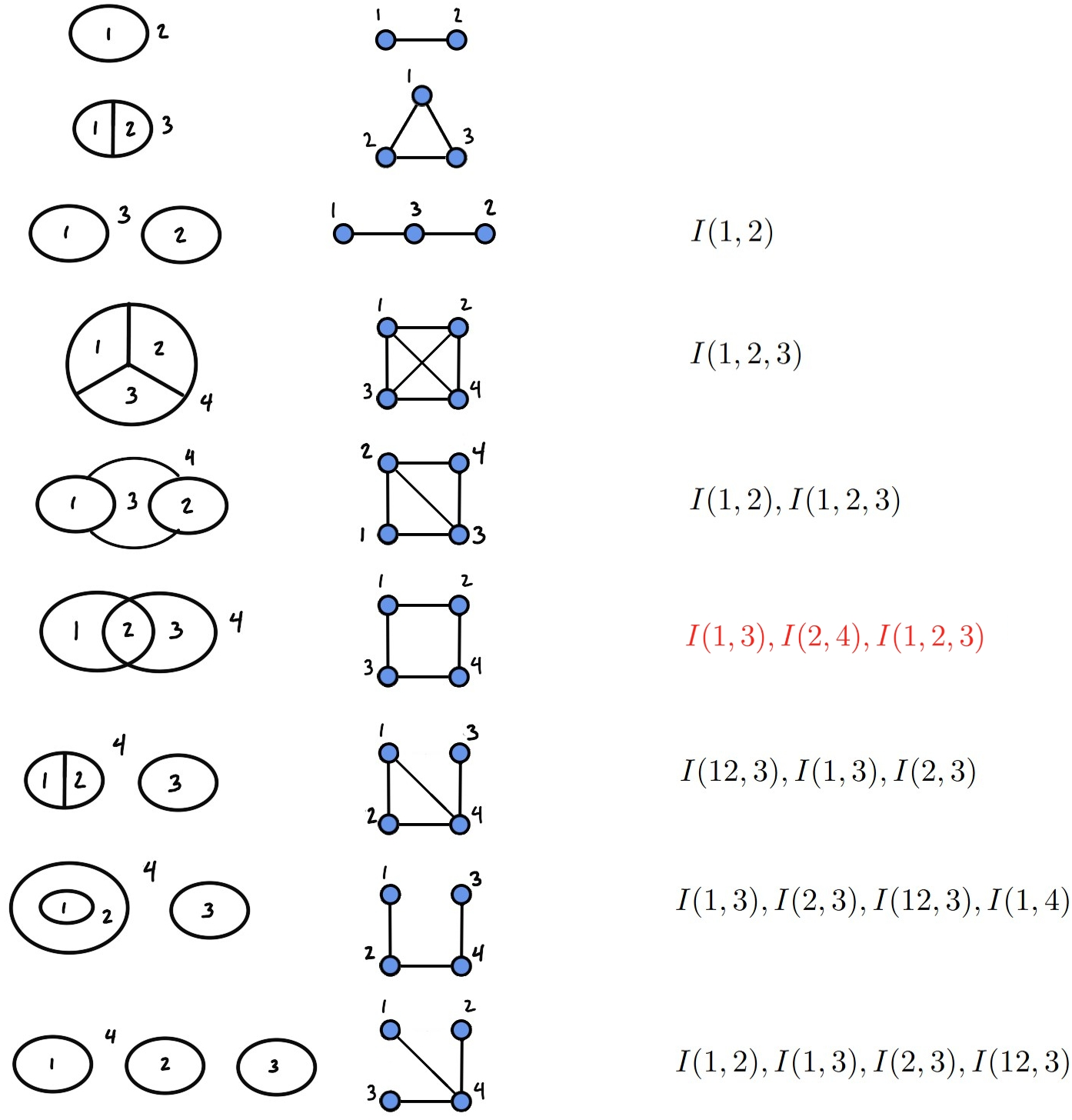
Figure 4: Example regions, associated graphs, and bases of entropy sums for which divergences associated with codimension-one boundaries cancel. Quantities in red have divergences associated with higher-order intersections and must be excluded to form a basis of fully finite entropy sums.

Higher-Codimension Divergences and Hypergraph Generalization

Beyond codimension-one divergences, additional divergences can arise from higher-codimension intersections (e.g., corners where three or more regions meet). The paper generalizes the graph-theoretic approach to hypergraphs, where hyperedges represent multi-region intersections. The divergence cancellation conditions are then expressed as further constraints on the Fourier coefficients, specifically requiring that coefficients associated with even-order subsets of intersection regions are equal.

This leads to a refined classification: mutual information is only finite if the two regions are non-adjacent even at higher-codimension intersections, and tripartite information is only finite if the three regions do not all meet at a common intersection with a fourth region. The paper provides explicit criteria for when these information measures are divergence-free.

Figure 5: Left: $I(A,B)$ has cancelling codimension-one divergences but uncancelled corner divergences. Middle: sufficiently cuspy corners may avoid additional divergences. Right: $I(A,B,C)$ has cancelling codimension-one divergences but uncancelled corner divergences.

Algebraic and Quantum Information-Theoretic Reformulation

The paper also discusses algebraic definitions of divergence-free entropy combinations using the framework of operator algebras and relative entropy. For example, the mutual information can be defined as the Araki relative entropy between the global state and the product of reduced states, provided the split property holds. The entropy difference $S(A) - S(A^c)$ can be expressed in terms of modular Hamiltonians and relative entropies, which are well-defined even for type III algebras.

Furthermore, the space of finite entropy sums is shown to be isomorphic to the ground state space of a specific Hamiltonian on $n$ qubits, with the divergence cancellation conditions corresponding to the vanishing of certain matrix elements. This provides a quantum information-theoretic perspective on the classification problem.

Implications, Limitations, and Future Directions

The results provide a rigorous and exhaustive classification of all linear combinations of entanglement entropies that are finite in local QFTs, under widely accepted assumptions about the structure of divergences. This has direct implications for the paper of topological entanglement entropy, area laws, and the extraction of universal data from entanglement measures in QFT and many-body systems.

Strong claims in the paper include:

• All finite entropy sums with codimension-one divergence cancellation are linear combinations of the three basic types.
• The explicit bases constructed are complete and orthogonal, with dimension $2^n - |E|$ (or $2^n - |I_E|$ for hypergraphs).
• For certain hypergraphs, the information-theoretic basis is not sufficient to span the space of all finite entropy sums, necessitating more general linear combinations.

Limitations: The analysis is purely mathematical and does not constitute a proof that the stated conditions are necessary and sufficient for divergence cancellation in all QFTs; rather, it assumes the standard structure of divergences. The algebraic definitions for tripartite information in the fully adjacent case remain an open problem.

Future directions include:

• Extending the algebraic definitions to all cases, including fully adjacent regions.
• Investigating the physical interpretation and utility of the more general finite entropy sums that are not simple information-theoretic quantities.
• Applying these results to the paper of entanglement in gauge theories, holographic systems, and systems with nontrivial topology.

Conclusion

This work provides a mathematically rigorous and physically motivated classification of all finite linear combinations of entanglement entropies in QFT, using graph and hypergraph theory, Boolean function analysis, and operator algebra techniques. The explicit bases and criteria developed here are directly applicable to the construction of universal entanglement measures and the analysis of entanglement structure in quantum many-body systems. The results also highlight the subtle interplay between geometry, combinatorics, and quantum information in the paper of entanglement in field theory.