Graph-R1: Unleashing LLM Reasoning with NP-Hard Graph Problems (2508.20373v1)

Abstract: Reasoning LLMs (RLLMs) have recently achieved remarkable progress on complex reasoning tasks, largely enabled by their long chain-of-thought (Long CoT) capabilities. However, developing these Long CoT behaviors relies heavily on post-training with high-quality datasets, which are typically costly and human-curated (e.g., mathematics and code), leaving scalable alternatives unexplored. In this work, we introduce NP-hard (NPH) graph problems as a novel synthetic training corpus, as they inherently require deep reasoning, extensive exploration, and reflective strategies, which are core characteristics of Long CoT reasoning. Building on this insight, we develop a two-stage post-training framework: (i) Long CoT Supervised Fine-Tuning (SFT) on rejection-sampled NPH graph instances, which substantially enhances reasoning depth, and (ii) Reinforcement Learning (RL) with a fine-grained reward design, which sharpens reasoning efficiency. Our flagship model, Graph-R1-7B, demonstrates strong generalization across mathematics, coding, STEM, and logic, and surpasses QwQ-32B on NPH graph problems in both accuracy and reasoning efficiency. These results position NPH graph problems as an effective and scalable resource for advancing Long CoT reasoning in LLMs, opening a new frontier for LLM post-training. Our implementation is available at https://github.com/Graph-Reasoner/Graph-R1, with models and datasets hosted in our Hugging Face collection HKUST-DSAIL/Graph-R1.

• The paper introduces a two-stage SFT and RL framework that uses NP-hard graph problems to significantly enhance long chain-of-thought reasoning in LLMs.
• It demonstrates notable improvements across multiple domains, with up to 16× accuracy gains and a 47.3% reduction in token usage compared to baseline models.
• The methodology employs fine-grained reward design and curriculum learning to reduce repetitive output while maintaining deep, systematic reasoning.

Graph-R1: Leveraging NP-Hard Graph Problems for Long Chain-of-Thought Reasoning in LLMs

Motivation and Theoretical Foundations

The paper introduces a principled approach for post-training LLMs to enhance their Long Chain-of-Thought (Long CoT) reasoning capabilities by leveraging NP-hard (NPH) graph problems as a synthetic training corpus. The rationale is that NPH graph problems inherently require deep logical reasoning, extensive exploration of solution spaces, and self-reflective strategies—core attributes of Long CoT reasoning. Unlike traditional post-training corpora (e.g., mathematics, code), which are costly and human-curated, NPH graph problems offer scalable, verifiable, and diverse synthetic data generation, enabling efficient and effective post-training.

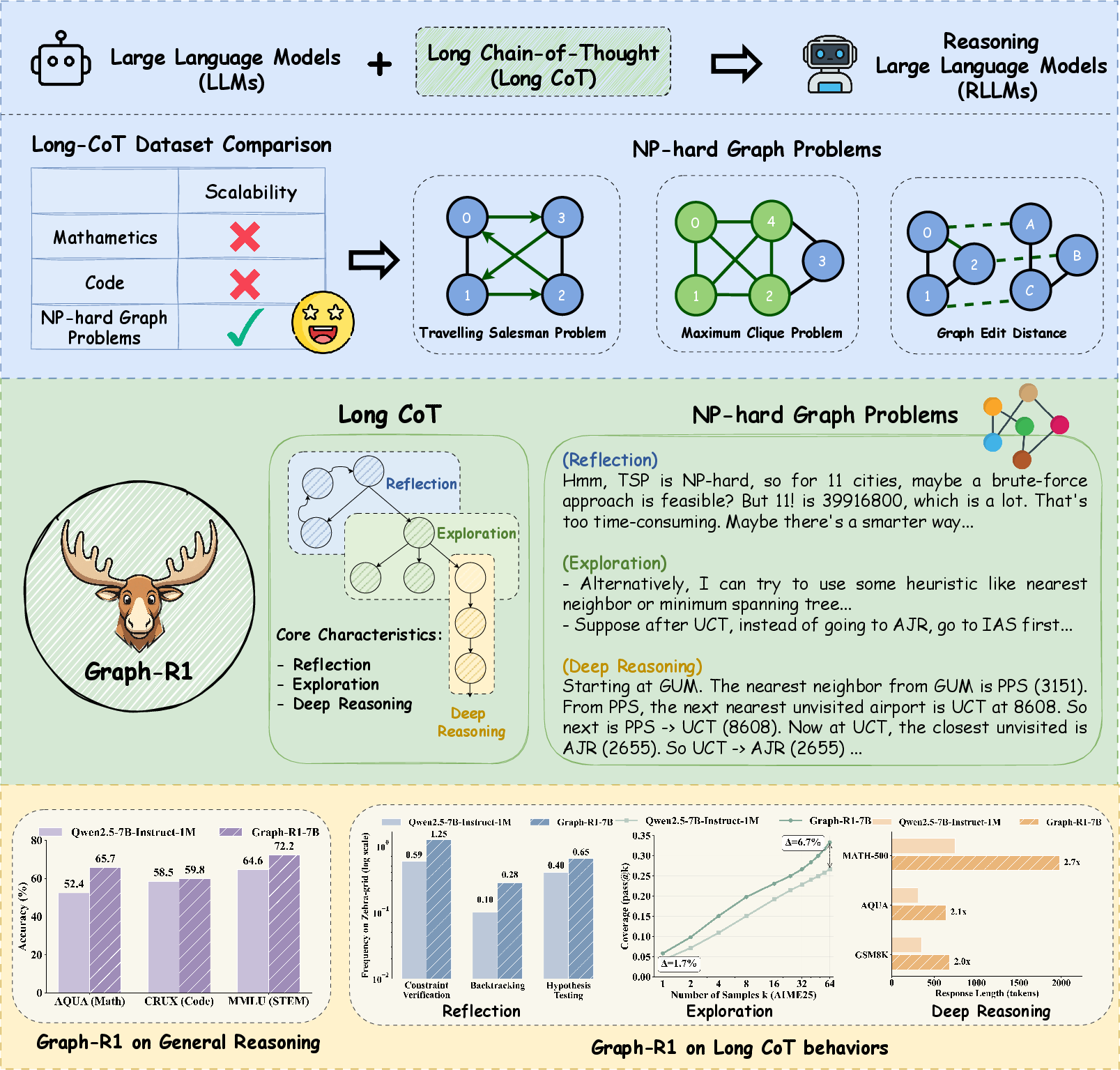
Figure 1: Overview of Graph-R1, illustrating the two-stage post-training pipeline and the integration of NP-hard graph problems as the central training corpus.

Methodology: Two-Stage Post-Training Framework

The Graph-R1 framework consists of two sequential stages:

1. Long CoT Supervised Fine-Tuning (SFT):
   • Construction of a high-quality Long CoT dataset by prompting a strong teacher model (QwQ-32B) with NPH graph problems and applying multi-stage rejection sampling for correctness and feasibility.
   • SFT is performed on base models (Qwen2.5-7B-Instruct-1M and Qwen2.5-1.5B), training them to generate systematic, step-by-step reasoning traces for graph problems.
   • This stage substantially increases reasoning depth and response length but introduces reasoning redundancy.
2. Reinforcement Learning (RL) with Fine-Grained Reward Design:
   • RL is applied to address inefficiency and redundancy in reasoning traces.
   • The reward function comprises three components: repetition penalty (to suppress redundant reasoning), solution quality reward (to incentivize concise, high-quality solutions), and format reward (to promote structured reasoning).
   • Group Relative Policy Optimization (GRPO) is adopted for computational efficiency, combined with curriculum learning to control token budget and scale difficulty.

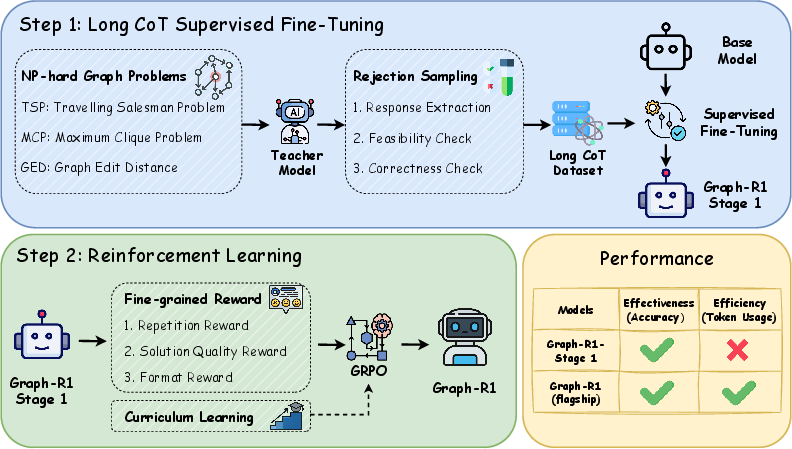
     Figure 2: Methodology of Graph-R1, detailing the SFT and RL stages, reward design, and curriculum learning strategy.

Empirical Results: Generalization and Efficiency

General Reasoning Tasks

Graph-R1-7B demonstrates strong generalization across mathematics, coding, STEM, and logic reasoning tasks, consistently outperforming its base model and competitive baselines. Notable improvements include:

• Mathematical Reasoning:
  • AQUA: +13.3% absolute gain (65.7% vs. 52.4%)
  • Zebra-grid: +21.4% relative gain (11.9% vs. 9.8%)
  • AIME25 pass@64: +6.6% over base model
• Graph Reasoning:
  • Shortest Distance: 52.0% vs. 29.6%
  • Common Neighbor: 87.0% vs. 54.0%
• STEM and Logic:
  • MMLU_STEM: 72.2% vs. 64.6%

NP-Hard Graph Problems

On both small-scale and large-scale NPH graph problems, Graph-R1-7B achieves the highest average accuracy among all baselines, including QwQ-32B and graph-specialized models. Notably, Graph-R1-7B generalizes from small-scale training to large-scale evaluation, achieving a 16× improvement over its base model on large-scale instances and surpassing its teacher model.

Token Efficiency

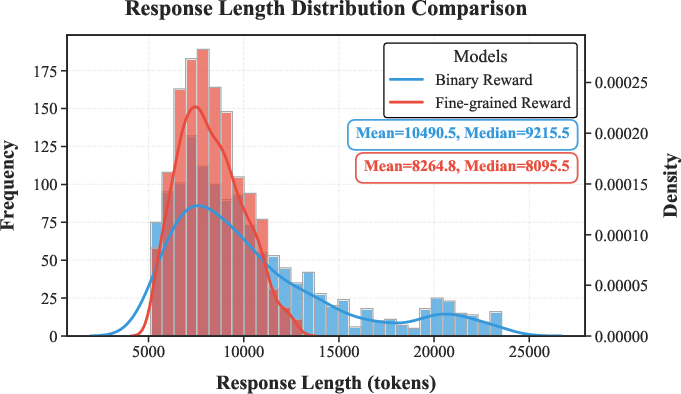
Graph-R1-7B exhibits superior token efficiency, requiring only 8,264 tokens on average—a 47.3% reduction compared to QwQ-32B (15,684 tokens)—while maintaining or improving solution accuracy.

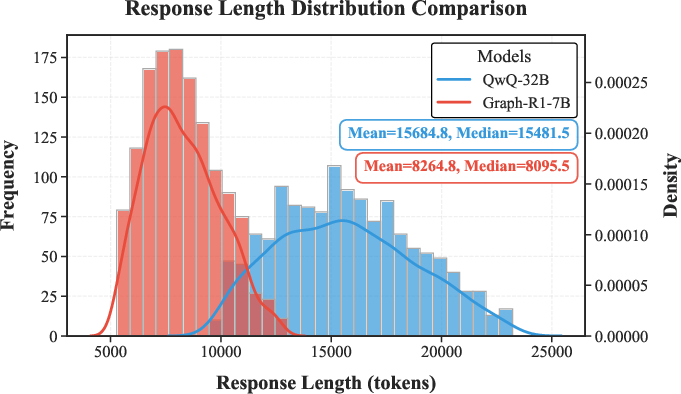
Figure 3: Token efficiency comparison between Graph-R1-7B and QwQ-32B, highlighting substantial reduction in token usage.

Analysis of Long CoT Capabilities

The paper provides quantitative evidence that Graph-R1 models exhibit the three core characteristics of Long CoT reasoning:

• Deep Reasoning:
  • Substantial increase in response length (e.g., 6.6× longer on AIME25), indicating more thorough problem decomposition.
• Extensive Exploration:
  • Higher pass@k metrics on challenging benchmarks, reflecting broader search of solution space.
• Feasible Reflection:
  • Marked rise in self-reflection frequency (verification, backtracking, heuristics), as measured by LLM-as-a-judge analysis.
  • 

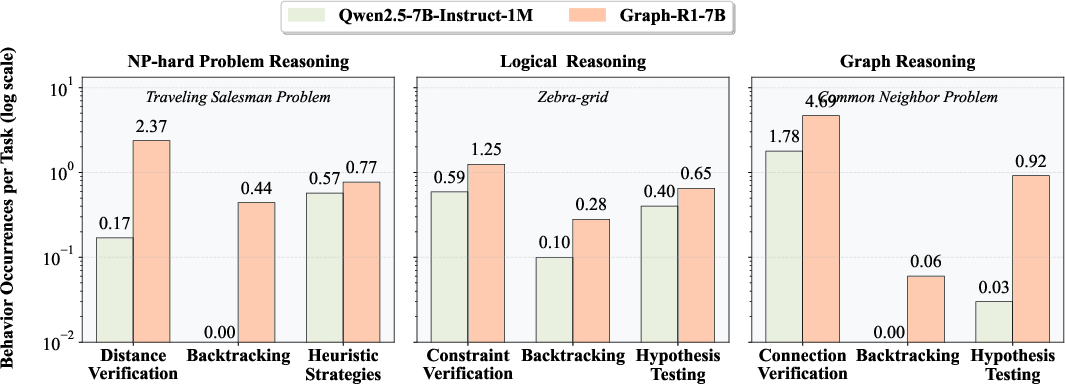
  • Figure 4: Self-reflection behavior statistics before and after training, showing increased frequency of verification, backtracking, and heuristic strategies.

Ablation Studies and Reward Design

Ablation studies confirm the necessity of both SFT and RL stages:

• SFT alone increases reasoning length and accuracy but introduces severe repetition and inefficiency.
• RL with fine-grained reward design reduces token usage by 56.2% and improves accuracy on tasks where SFT alone underperforms.
• The fine-grained reward function (vs. binary reward) further reduces response length by 21% and increases solution feasibility.

  Figure 5: Ablation paper on fine-grained reward, demonstrating improved token efficiency and solution feasibility.

Curriculum learning in RL reduces token consumption by ~30% without compromising validation performance.

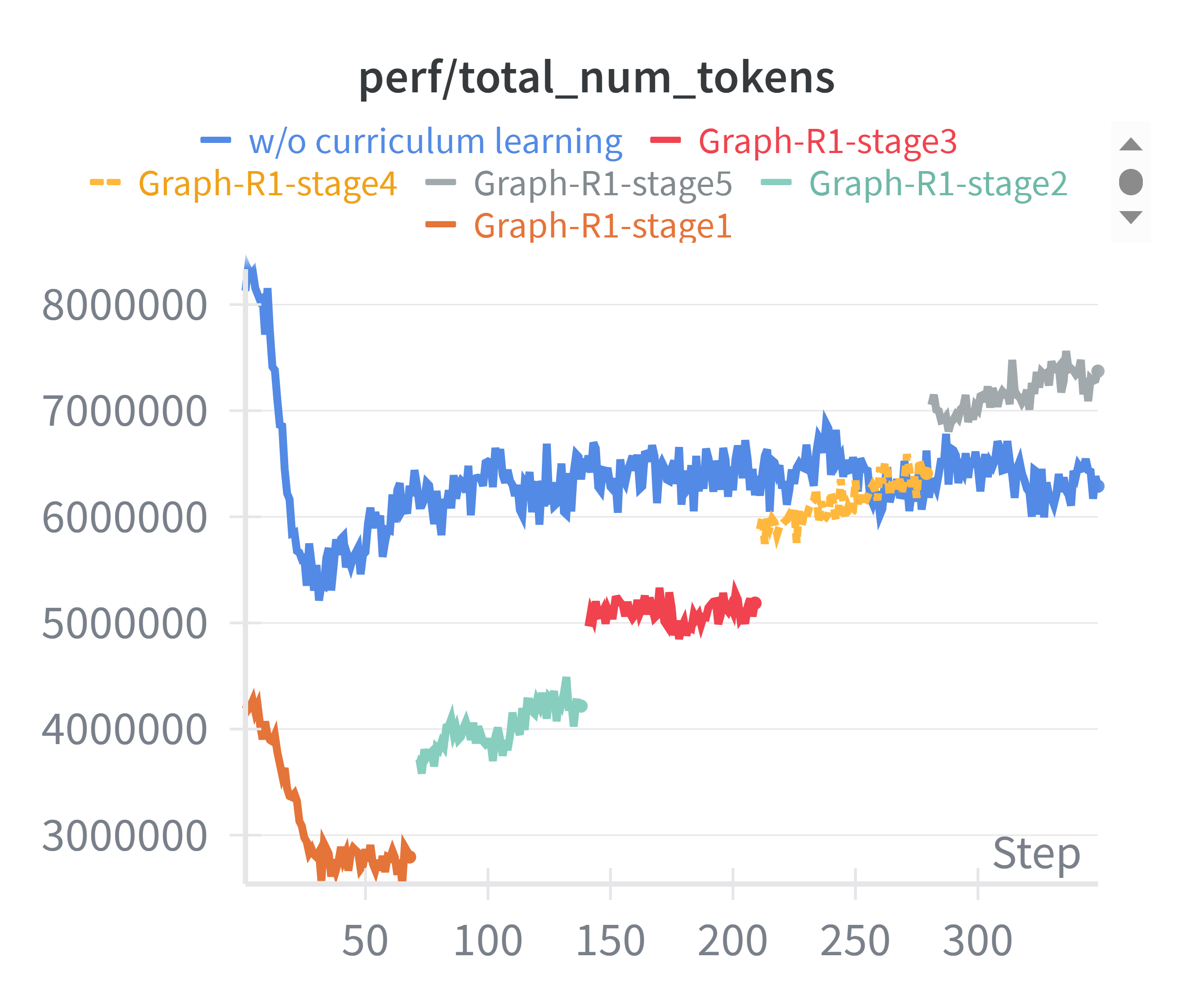
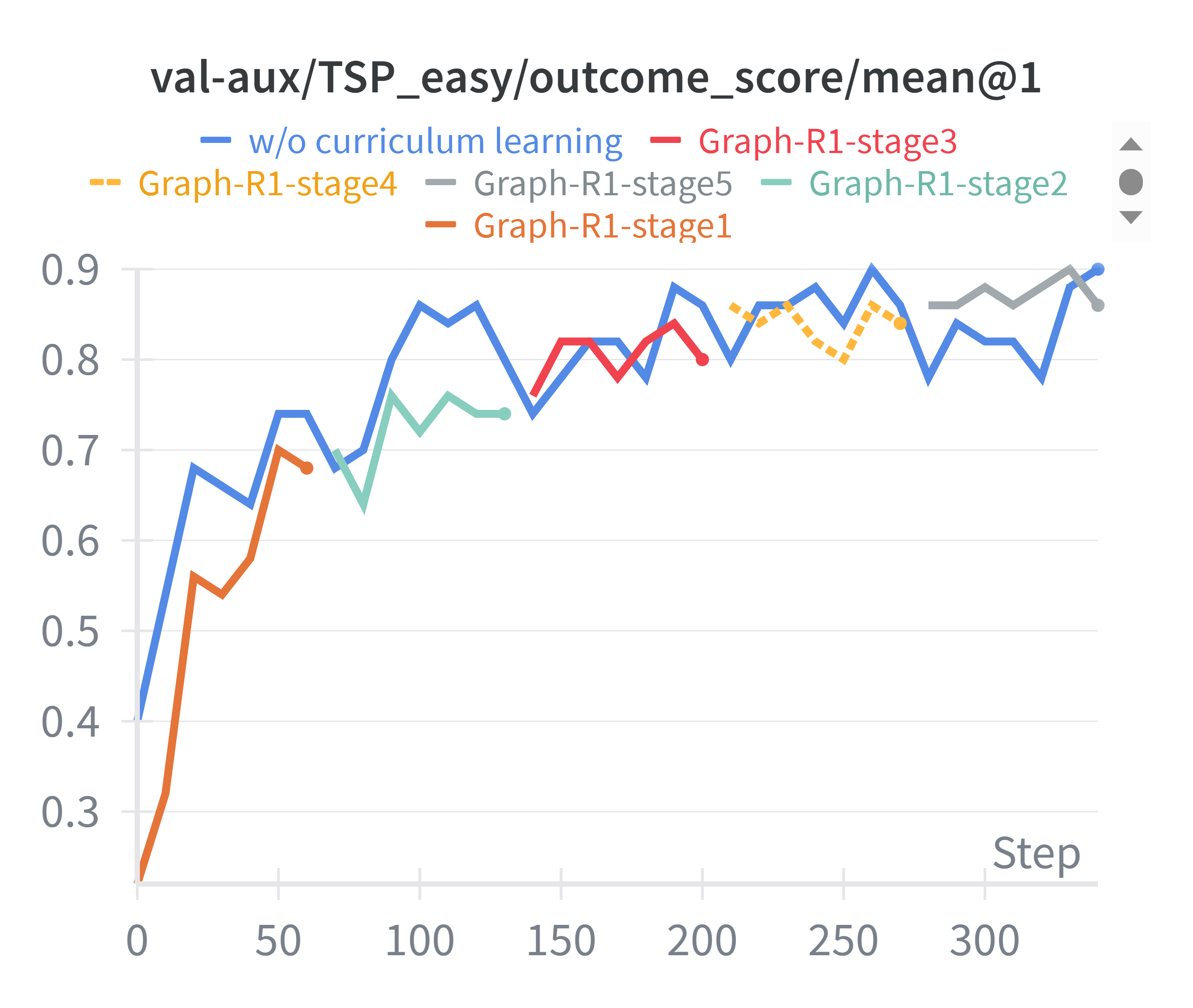
Figure 6: Token consumption comparison between curriculum learning and mixed-difficulty training.

Comparative Analysis: Repetition and Baseline Efficiency

Graph-R1 models maintain low repetition probability (<5%) across all temperature settings, outperforming reasoning baselines by large margins.

Figure 7: Token efficiency comparison with all baselines, showing Graph-R1's favorable balance of accuracy and output compactness.

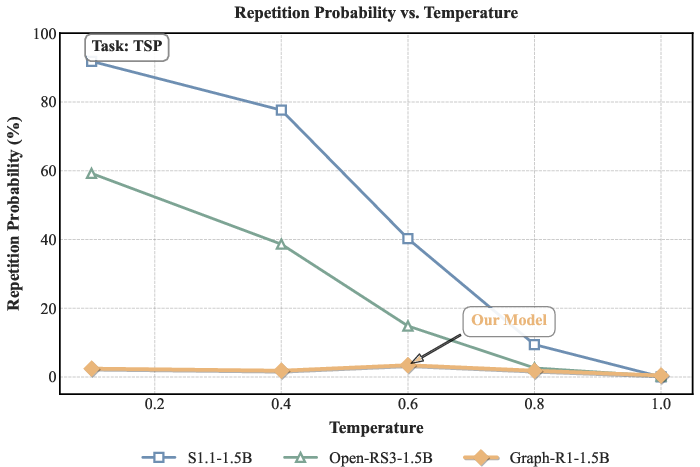
Figure 8: Repetition probability comparison, illustrating Graph-R1's robustness against repetitive reasoning.

Qualitative Case Studies

Case studies on TSP and logic puzzle tasks illustrate the model's ability to perform deep, reflective, and structured reasoning, with explicit verification and backtracking steps.

Figure 9: Case paper for TSP task, demonstrating stepwise reasoning and self-correction.

Figure 10: Case paper for Logic Puzzle task, highlighting constraint validation and hypothesis testing.

Implications and Future Directions

The results position NP-hard graph problems as a scalable and effective corpus for eliciting transferable Long CoT reasoning in LLMs. The demonstrated generalization across domains suggests that synthetic graph tasks can serve as a universal substrate for reasoning post-training, reducing reliance on costly human-curated datasets. The fine-grained reward design and curriculum learning strategies provide practical guidance for efficient RL-based post-training.

Theoretical implications include the identification of NPH graph problems as a driver for cross-domain generalization, and the empirical validation of Long CoT reasoning as a mechanism for transfer. Practically, the approach enables the development of compact, efficient, and highly capable reasoning models suitable for deployment in resource-constrained environments.

Future work should expand the diversity of NPH graph problems in the training corpus and explore alternative post-training paradigms beyond SFT+RL, such as unsupervised or self-improving frameworks. Further investigation into the mechanisms of transfer and the scaling laws of reasoning ability with respect to data volume and difficulty distribution is warranted.

Conclusion

Graph-R1 establishes a robust framework for post-training LLMs using NP-hard graph problems, achieving strong improvements in reasoning effectiveness and efficiency. The two-stage SFT+RL pipeline, fine-grained reward design, and curriculum learning collectively enable the development of models with advanced Long CoT capabilities and broad generalization. The work provides both theoretical and practical insights into scalable reasoning post-training and opens new avenues for research in universal reasoning model development.