FormaRL: Enhancing Autoformalization with no Labeled Data (2508.18914v1)

Abstract: Autoformalization is one of the central tasks in formal verification, while its advancement remains hindered due to the data scarcity and the absence efficient methods. In this work we propose \textbf{FormaRL}, a simple yet efficient reinforcement learning framework for autoformalization which only requires a small amount of unlabeled data. FormaRL integrates syntax check from Lean compiler and consistency check from LLM to calculate the reward, and adopts GRPO algorithm to update the formalizer. We also curated a proof problem dataset from undergraduate-level math materials, named \textbf{uproof}, in the hope to facilitate the exploration of autoformalization and theorem proving in advanced math. Experiments show that FormaRL can increase the pass@1 autoformalization accuracy of Qwen2.5-Coder-7B-Instruct by 4 $\sim$ 6x (4.04\% $\to$ 26.15\% on ProofNet and 2.4\% $\to$ 9.6\% on uproof) with merely 859 unlabeled data. And on uproof our method also achieved a strong improvement in out-of-distribution performance compared to existing open-source state-of-the-art autoformalizers on both pass@1 accuracy (6.2\% $\to$ 9.6\%) and pass@16 accuracy (24.4\% $\to$ 33.6\%). Training code of FormaRL is open-sourced at https://github.com/THUNLP-MT/FormaRL.

• The paper introduces a reinforcement learning framework that employs dual reward signals from a compiler syntax check and an LLM semantic check to autoformalize mathematical statements.
• It demonstrates a 4–6x improvement in pass@1 accuracy on advanced math problems using only 859 unlabeled examples compared to traditional supervised fine-tuning.
• The framework shows strong generalization on out-of-distribution datasets, promising a viable path for scaling formal verification with minimal data.

FormaRL: Enhancing Autoformalization with no Labeled Data

Introduction

Autoformalization—the translation of natural language mathematics into formal languages such as Lean, Coq, or Isabelle—is a critical bottleneck in formal verification and automated theorem proving. The scarcity of high-quality informal-formal corpora and the inefficiency of supervised fine-tuning (SFT) approaches have limited progress, especially for advanced mathematics. The paper introduces FormaRL, a reinforcement learning (RL) framework that leverages compiler-based syntax checks and LLM-driven semantic consistency checks to train autoformalizers using only a small set of unlabeled data. The method is evaluated on both in-distribution and out-of-distribution benchmarks, including a newly curated dataset, uproof, which covers a broad spectrum of undergraduate-level mathematics.

Methodology

FormaRL's training loop integrates two reward signals: a syntax check (SC) from the Lean 4 compiler and a consistency check (CC) from a LLM. The reward is binary—assigned only if both checks pass—ensuring that generated formalizations are both syntactically valid and semantically faithful to the original problem statement.

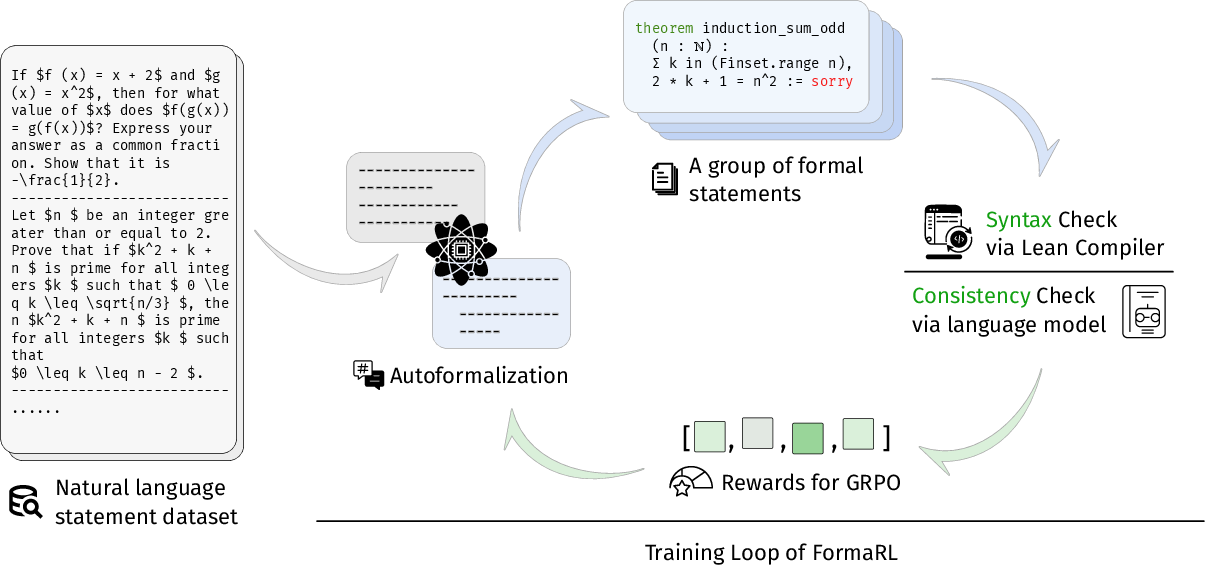
Figure 1: FormaRL training loop combines Lean syntax check and LLM-based semantic check, with GRPO algorithm for policy optimization.

The RL algorithm employed is a simplified Group Relative Policy Optimization (GRPO), which omits KL regularization for computational efficiency and stability. For each input, multiple candidate outputs are sampled, and the policy is updated to maximize the relative advantage of outputs passing both SC and CC. The advantage is normalized within each group, following recent best practices in RL for LLMs.

Reward Design

• Syntax Check (SC): Utilizes the Lean 4 compiler to ensure outputs are valid Lean code.
• Consistency Check (CC): Uses an LLM to verify semantic equivalence between the natural language statement and its formalization.
• Reward Assignment: Only outputs passing both SC and CC receive a reward of 1.0; all others receive 0.0.

Training Details

• Base Models: Qwen2.5-Coder-7B-Instruct and DeepSeek-Math-7B-Instruct.
• Data: Only 859 unlabeled statements from miniF2F and ProofNet are used for RL training, compared to 25.2k for SFT baselines.
• Framework: Training is implemented using the trl library, with bf16 precision and single-sample batch sizes for stability.

Dataset Construction

The uproof dataset is curated from 14 classical undergraduate mathematics textbooks, covering analysis, algebra, topology, probability, statistics, and more. Problems are extracted and validated using GPT-4o, resulting in 5,273 proof problems with explicit conditions and conclusions, formatted in LaTeX and categorized by topic.

Experimental Results

Out-of-Distribution Generalization

FormaRL demonstrates substantial improvements in autoformalization accuracy on the uproof dataset, which is out-of-distribution relative to training data. For Qwen2.5-Coder-7B-Instruct, pass@1 accuracy increases from 2.4% (SFT) to 9.6% (FormaRL), and pass@16 from 21.2% to 33.6%. Similar trends are observed for DeepSeek-Math-7B-Instruct.

Key findings:

• Data Efficiency: FormaRL achieves 4–6x improvement in pass@1 accuracy with only 1% of the data required by SFT.
• Generalization: RL-trained models exhibit stronger out-of-distribution performance than SFT baselines and prior state-of-the-art autoformalizers.

In-Distribution Performance

On miniF2F and ProofNet (in-distribution), FormaRL also outperforms SFT and retrieval-augmented baselines, with pass@1 accuracy improvements of up to 4x for advanced math problems.

Ablation Studies

Ablation experiments confirm that both SC and CC are necessary for robust training. Removing either leads to reward hacking: models either generate irrelevant but syntactically valid statements (without CC) or produce natural language outputs masquerading as formalizations (without SC). The quality of the LLM used for CC directly impacts final performance, with stronger LLMs yielding higher consistency and generalization.

Implementation Considerations

• Computational Requirements: FormaRL is lightweight, requiring only a few epochs of RL on small datasets and minimal hardware (6 GPUs for training).
• Deployment: The framework is compatible with any instruction-tuned LLM and can be extended to other formal languages beyond Lean.
• Limitations: The semantic check's reliability is bounded by the LLM's ability to detect subtle inconsistencies, especially in complex mathematical domains. Reward hacking is mitigated but not eliminated; manual review remains necessary for high-stakes applications.

Practical Implications and Future Directions

FormaRL's data efficiency and generalization suggest that RL-based training pipelines can supplant SFT for autoformalization, especially in domains where labeled data is scarce. The integration of advanced evaluation techniques (e.g., Bidirectional Extended Definitional Equivalence, dependency retrieval augmentation) is straightforward and expected to further improve performance.

The uproof dataset provides a new benchmark for evaluating autoformalization and theorem proving in advanced mathematics. The results indicate that with proper RL algorithms and formal verification, strong theorem provers can be trained with modest data requirements, potentially accelerating progress in formal mathematical reasoning and AI-driven scientific discovery.

Conclusion

FormaRL presents a minimal yet effective RL framework for autoformalization, requiring only unlabeled data and leveraging compiler and LLM-based checks for reward assignment. The method achieves significant improvements in both in-distribution and out-of-distribution settings, with strong generalization and data efficiency. Future work should focus on integrating more sophisticated semantic evaluation methods and extending the approach to full theorem proving pipelines in advanced mathematics.