A Scalable Heuristic for Molecular Docking on Neutral-Atom Quantum Processors (2508.18147v1)

Abstract: Molecular docking is a critical computational method in drug discovery used to predict the binding conformation and orientation of a ligand within a protein's binding site. Mapping this challenge onto a graph-based problem, specifically the Maximum Weighted Independent Set (MWIS) problem, allows it to be addressed by specialized hardware such as neutral-atom quantum processors. However, a significant bottleneck has been the size mismatch between biologically relevant molecular systems and the limited capacity of near-term quantum devices. In this work, we overcome this scaling limitation by the use of a novel divide-and-conquer heuristic introduced in Cazals et al. This algorithm enables the solution of large-scale MWIS problems by decomposing a single, intractable graph instance into smaller sub-problems that can be solved sequentially on a neutral-atom quantum emulator, incurring only a linear computational overhead. We demonstrate the power of this approach by solving a 540-node MWIS problem representing the docking of an inhibitor to the Tumor necrosis factor-$\alpha$ Converting Enzyme--thiol-containing Aryl Sulfonamide (TACE-AS) complex. Our work enables the application of quantum methods to more complex and physically realistic molecular systems than previously possible, paving the way for tackling large-scale docking challenges on near-term quantum hardware.

• The paper reformulates the docking problem as a Maximum Weighted Independent Set (MWIS) instance on a binding interaction graph to capture ligand-receptor interactions.
• The paper develops a divide-and-conquer heuristic that decomposes non-embeddable graphs into smaller, quantum-embeddable subgraphs using neutral-atom processors.
• The paper validates the approach on a 540-node instance, achieving optimal MWIS weights comparable to classical solvers and outperforming standard greedy heuristics.

Scalable Quantum Heuristics for Molecular Docking: Graph-Based Formulation and Neutral-Atom Implementation

Introduction

This work presents a comprehensive pipeline for molecular docking using neutral-atom quantum processors, addressing the scaling bottleneck that has historically limited quantum approaches to toy models. The authors reformulate the docking problem as a Maximum Weighted Independent Set (MWIS) instance on a graph encoding ligand-receptor pharmacophore interactions, and introduce a divide-and-conquer heuristic that decomposes large, non-embeddable graphs into tractable subgraphs suitable for quantum emulation. The methodology is validated on a 540-node instance representing the TACE-AS complex, demonstrating parity with optimal classical solvers and outperforming standard greedy heuristics.

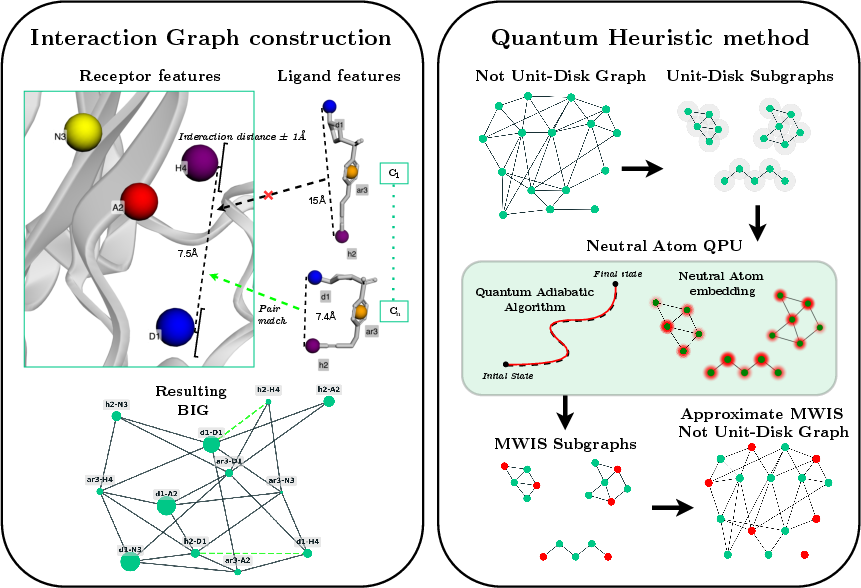
Figure 1: Schematic of the end-to-end workflow: from pharmacophore extraction and conformer generation to graph construction, quantum subgraph decomposition, and docking pose reconstruction.

Graph-Based Formulation of Molecular Docking

The docking problem is abstracted as a combinatorial optimization task by constructing a Binding Interaction Graph (BIG). Vertices represent possible ligand-receptor pharmacophore pairs, weighted by knowledge-based interaction potentials derived from statistical analysis of protein-ligand complexes. Edges encode geometric compatibility, determined by the spatial arrangement of pharmacophores and ligand flexibility.

Physically-Aware Graph Construction

Three key enhancements are introduced to improve the physical realism of the BIG:

1. Expanded Interaction Scope: The spatial cutoff for receptor pharmacophore selection is increased to 6.5 Å, ensuring comprehensive coverage of the binding site.
2. Solvent Accessibility Filtering: Pharmacophores are filtered using solvent-accessible surface area (SASA) metrics, excluding buried, sterically inaccessible points.

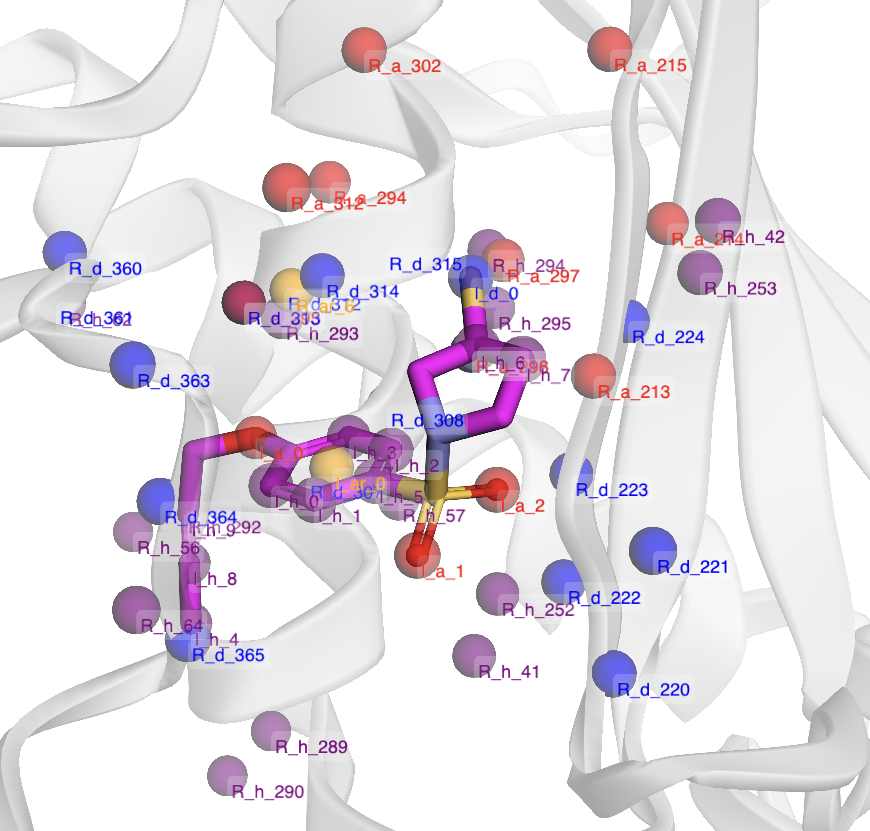
   Figure 2: Pharmacophore points within the binding site, colored by feature type and filtered for solvent accessibility.

   

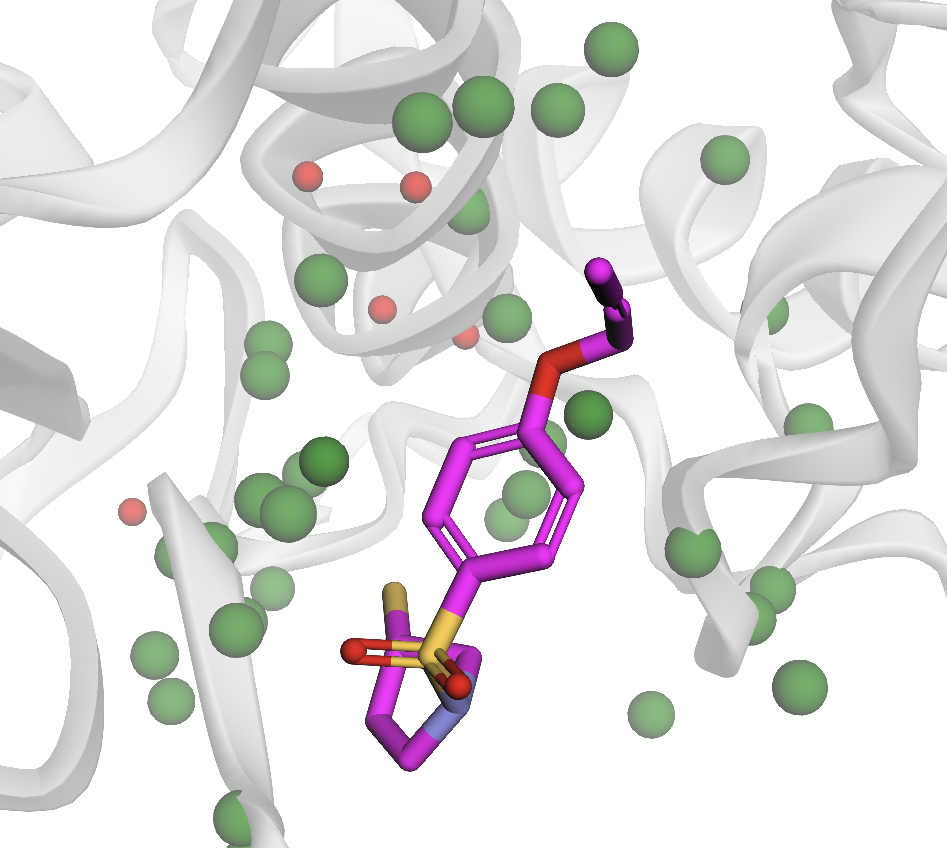
   Figure 3: SASA filtering of receptor pharmacophores, highlighting retained (green) and excluded (red) points.

3. Ligand Flexibility via Conformational Ensembles: Ligand conformers are generated using RDKit, and edge compatibility is defined over the ensemble, capturing realistic intramolecular distance variations.

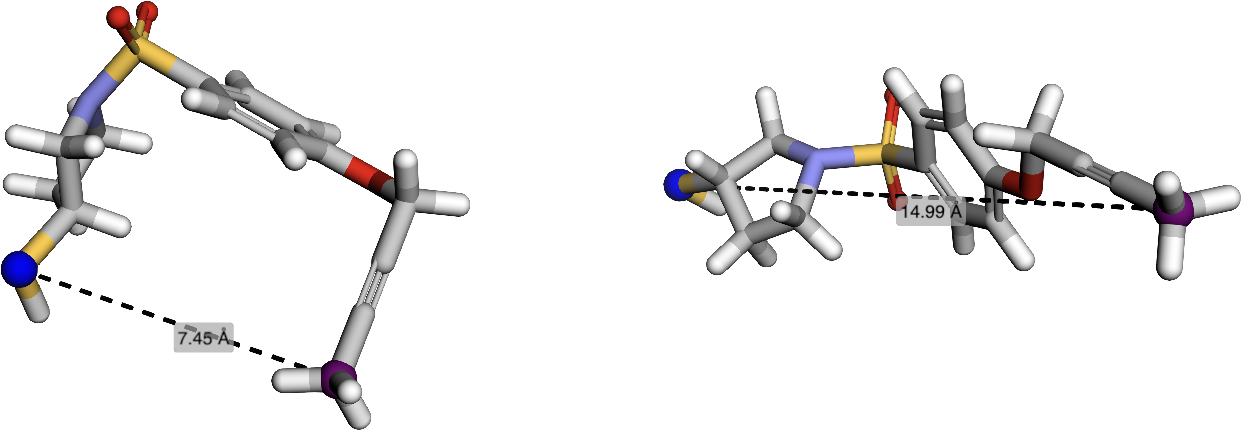
   Figure 4: Visualization of ligand conformational flexibility, showing two low-energy conformers and the largest pharmacophore distance variation.

Quantum MWIS Solving on Neutral-Atom Processors

The MWIS problem is mapped to the physical constraints of neutral-atom quantum processors, leveraging the Rydberg blockade mechanism to enforce independent set constraints. The cost function is encoded in the Hamiltonian via local detuning, with vertex weights mapped to detuning amplitudes and edge constraints realized through spatial atom arrangement.

Divide-and-Conquer Heuristic for Non-Embeddable Graphs

The BIG is typically non-unit-disk (non-UD), precluding direct embedding. The authors implement a recursive decomposition heuristic (GLS mapping), extracting maximal embeddable UD subgraphs, solving MWIS on each via quantum annealing emulation, and merging solutions to construct a global independent set. Hyperparameters (number of subgraphs, branches, solutions per step) are tuned to optimize performance.

Numerical Results and Docking Reconstruction

The pipeline is benchmarked on a 540-node, 48,151-edge BIG for the TACE-AS complex. The quantum heuristic achieves the optimal MWIS weight (5.4), matching the CPLEX solver and outperforming the greedy algorithm (4.63, 14.29% gap). Subgraph sizes range from 8 to 18 vertices, demonstrating the scalability of the approach.

Docking pose reconstruction is performed by selecting the conformer that best aligns the ligand pharmacophores to the receptor points via the Kabsch algorithm. The resulting pose yields an RMSD of 7.71 Å relative to the crystallographic structure, exceeding the typical threshold for correct predictions.

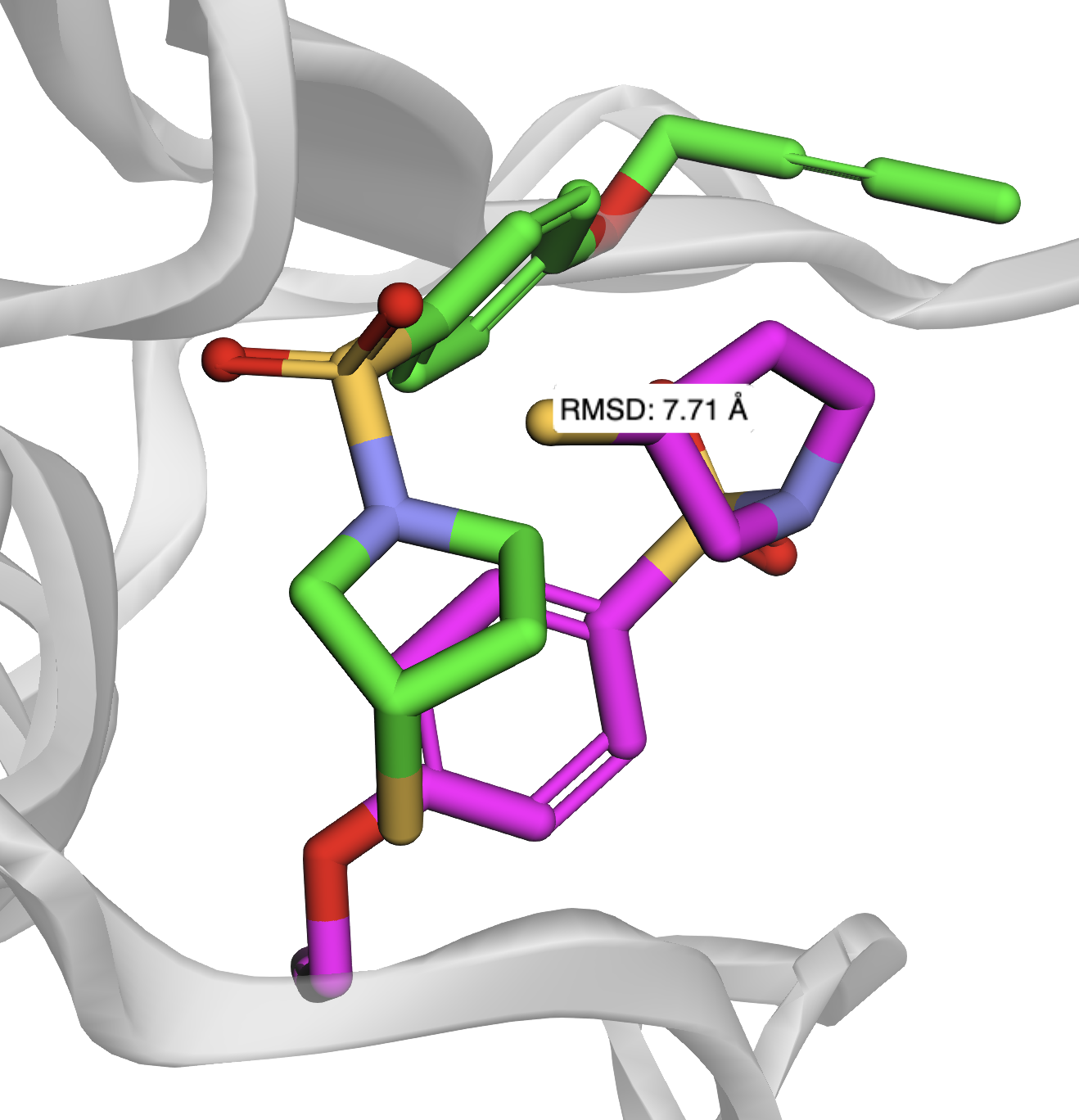
Figure 5: Final docked ligand position (green) versus crystallographic pose (magenta), RMSD = 7.71 Å.

Discussion

The quantum heuristic enables large-scale graph optimization on neutral-atom hardware, circumventing the reduction overhead of previous approaches. The method is robust, matching optimal classical solutions for MWIS on realistic molecular systems. However, the discrete graph model introduces a disconnect between optimal interaction sets and physically accurate docking poses, as evidenced by the high RMSD. This is attributed to the lack of explicit penalization for unfavorable interactions (e.g., steric clashes) and the abstraction of continuous molecular forces.

The pipeline delineates the boundary between combinatorial optimization and physical modeling, suggesting that hybrid approaches—combining quantum global search with classical refinement—are necessary for accurate docking. Future work should focus on enriching the graph model with negative constraints and integrating free-energy-like scoring functions.

Conclusion

This paper establishes a scalable, physically-aware workflow for molecular docking on neutral-atom quantum processors, demonstrating that quantum heuristics can solve large MWIS instances at parity with classical solvers. While the current abstraction limits direct translation to accurate docking poses, the approach provides a foundation for hybrid quantum-classical pipelines in drug discovery and molecular design. Further refinement of the interaction graph and integration of physical constraints are required to bridge the gap between combinatorial optimization and molecular realism.