Challenges in Statistics: A Dozen Challenges in Causality and Causal Inference (2508.17099v1)

Abstract: Causality and causal inference have emerged as core research areas at the interface of modern statistics and domains including biomedical sciences, social sciences, computer science, and beyond. The field's inherently interdisciplinary nature -- particularly the central role of incorporating domain knowledge -- creates a rich and varied set of statistical challenges. Much progress has been made, especially in the last three decades, but there remain many open questions. Our goal in this discussion is to outline research directions and open problems we view as particularly promising for future work. Throughout we emphasize that advancing causal research requires a wide range of contributions, from novel theory and methodological innovations to improved software tools and closer engagement with domain scientists and practitioners.

• The paper presents a comprehensive survey of 12 open challenges in causal inference, spanning issues from experimental design to heterogeneous effects.
• The study synthesizes three formal frameworks—potential outcomes, SEMs, and graphical models—highlighting their overlaps and limitations in mapping assumptions to effects.
• It emphasizes the urgent need for scalable automation, robust sensitivity analysis, and AI integration to address complex causal problems in modern statistics.

Challenges in Statistics: A Dozen Challenges in Causality and Causal Inference

Introduction and Historical Context

The paper provides a comprehensive overview of the maturation and expansion of causality and causal inference into a central concern for statistics and affiliated fields. Three decades ago, causality was rarely addressed explicitly in mainstream statistical venues; now, dedicated journals, societies, and university centers are devoted to the subject. The central thesis is both a survey of progress and a prospectus of twelve significant, open research challenges ranging from experimental design in complex systems to automation and validation in the causal inference ecosystem.

Figure 1: Proportion of articles with the word "causal" in the title, abstract, or keywords in leading statistics journals from 1970 to 2024.

Fundamental Frameworks for Causality

The paper foregrounds the syncretism of three formal languages for causal inference—potential outcomes, structural equation models (SEMs), and graphical models (DAGs)—each serving both foundational and applied purposes. Despite the equivalence of many results between frameworks (given compatible assumptions), the mapping between assumptions and inferential statements is not always straightforward. The field predominantly focused on the estimation of an average causal effect (ATE) for a binary treatment under unconfoundedness, occasionally to the exclusion of settings with unmeasured confounding, longitudinal exposures, or complex, structured interventions.

Survey of the Dozen Challenges

1. Experimental Design in Complex Environments

Contemporary experimentation extends far beyond the classical agricultural or clinical paradigm, encompassing sequential/adaptive designs, high-dimensional treatments (e.g., texts or images), platform trials in medicine, and multi-faceted randomizations used by tech companies. Major open directions include optimality theory for sequential/interference-affected designs, the integration of adaptive experimental design with robustness guarantees, and systematization of AI in experimental planning.

2. Interference and Complex Systems

A central challenge is relaxing SUTVA (Stable Unit Treatment Value Assumption), with significant recent progress in exposure mappings, partial interference modules, and complex networks where effects propagate through observed and latent relationships. Notably, the development of graph-theoretic and potential outcome-based tools for bipartite and networked settings is incomplete; power calculation and external validity in the presence of general interference remain open.

3. Heterogeneous Effects and Policy Learning

Current work mostly addresses CATEs (conditional average treatment effects) under smoothness assumptions. However, many real-world mechanisms manifest non-smooth, sparse, high-dimensional, or non-Euclidean structure. Modern work with orthogonal learning, meta-learners, and policy optimization via empirical welfare maximization only partially addresses estimation/inference, particularly in high-dimensional, structured, or time-varying settings.

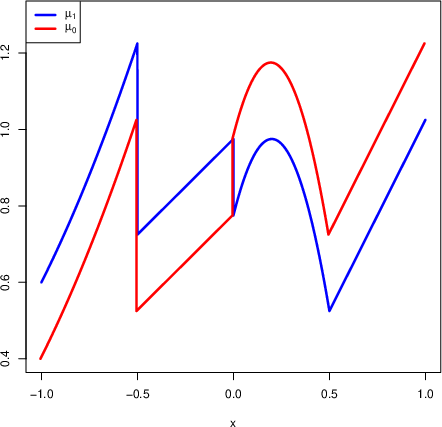
Figure 2: Example regression functions $\mu_w(x)=E[Y_i \mid X_i=x, W_i=w]$ demonstrating that the average causal effect can be zero while CATEs are non-trivial and highly structured.

4. Mediation and Causal Mechanisms

The field has advanced from linear path models to formal definitions (via nested counterfactuals) of direct and indirect (mediation) effects. Nevertheless, serious difficulties persist, e.g., in high-dimensional or time-varying mediation, identification under sequential randomization, and practical designs for causally interpretable mechanistic inference, especially in the presence of unmeasured confounding (requiring cross-world independence, which is inherently untestable).

5. Optimality and Minimaxity

The minimax theoretic program has yielded partial results on the rates for ATE/functional estimation, regression, and density deconvolution, which are dramatically slower in higher dimensions or under limited smoothness, especially when nuisance components (propensity, outcome models) are complex.

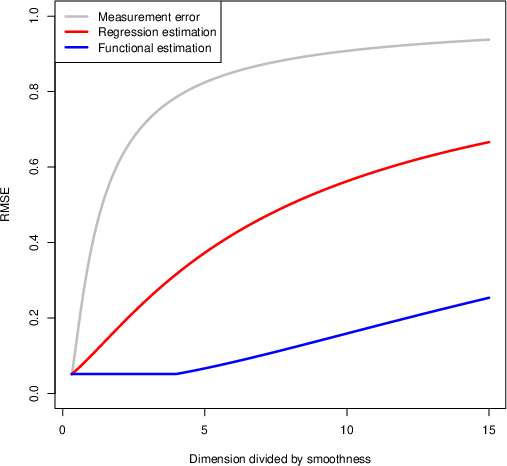
Figure 3: Minimax rates as functions of $d/s$ for estimation tasks: estimation of ATE, CATE, and measurement error density estimation, with distinct elbows where nonparametric rates degrade.

Crucially, foundational questions about attainable rates, adaptivity, and structure-agnostic estimation remain unanswered for many targets of substantive interest.

6. Sensitivity Analysis and Robustness

Despite consensus on the necessity of sensitivity analysis, methodological innovations (e.g., E-values, robustness benchmarks, bias-formula approaches) are not consistently adopted in empirical practice. Current debates focus on construction and reporting of robustness metrics, exploitation of domain knowledge, and generalizing sensitivity tools for multiple bias types (confounding, selection, measurement error).

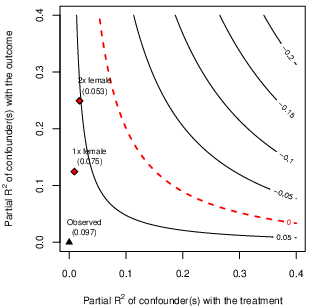
Figure 4: Example of a sensitivity contour plot with benchmarks—horizontal and vertical axes represent associations of potential confounders with treatment and outcome, respectively; plotted contours demonstrate bias-adjusted effects.

7. Reliable and Scalable Causal Discovery

Reliable causal discovery, especially in the presence of latent variables, selection, measurement error, and cycles, remains an active area, with constraint-based approaches struggling with the statistical complexity of high-order conditional independence testing. Major obstacles include error compounding across multiple CI tests, scalability to large systems, and valid post-selection inference.

8. Aggregation and Synthesis of Causal Knowledge

Synthesizing across studies, designs (randomized vs observational), and diverse populations is essential for external validity and policy action. Technical frontiers concern identification under provenance shifts, data fusion with covariate/variable mismatch, meta-analytic methods robust to design heterogeneity, and estimation under model uncertainty with unknown causal structure.

9. Automation in Causal Inference

Automation aims to transform causal inference by systematically representing and exploiting knowledge (assumptions, data, estimands), symbolic and numeric identification (e.g., do-calculus, ID algorithms, quantifier elimination, constraint satisfaction), and automated estimation with efficient uncertainty quantification. Only partial automation is realized—for linear or certain nonparametric models; incorporating shape constraints, constructing tractable representations, and scaling to large domains remain open.

10. Benchmarks, Evaluation, and Validation

Unlike prediction, causal inference suffers from the fundamental problem of missing counterfactuals, complicating benchmark construction and external validation. Efforts include quasi-experimental replications (e.g., LaLonde), synthetic and semi-synthetic datasets, and community challenges. Still, systematic benchmarks for high-dimensional, complex, or domain-specific data are lacking.

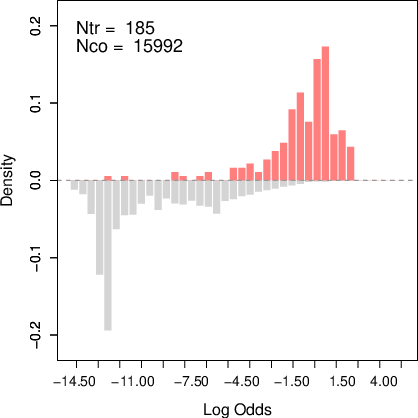
Figure 5: Assessing overlap in the LaLonde-Dehejia-Wahba data using log odds ratios—demonstrating critical overlap problems for causal effect estimation.

11. New Identification Strategies

Beyond standard identification via randomization, IV, and back-door, new strategies (e.g., synthetic controls, front-door, Mendelian randomization, negative control/proximal inference, panel data approaches) are being theoretically developed but their practical prevalence and statistical properties outside stylized settings require deeper analysis and empirical systematization.

12. Causal Inference Meets LLMs and Modern AI

The paper explores two-way interactions: using LLMs and generative models as components within the causal pipeline (for complex/structured text/image data, agentic simulations, and paper design copilot applications) and leveraging causality theory to improve AI robustness, fairness, preference learning, and interpretation via causal abstraction. Key research directions include validation of synthetic agents, causally-informative representation learning, and formal assessment of AI-aided causal discovery.

Cross-Cutting Theoretical and Practical Themes

• Domain Knowledge and Interdisciplinarity: Many causal questions require irreducible domain knowledge, yet robust frameworks for formal elicitation and integration are lacking.
• Theory-Practice Gap: Significant theoretical advances are underutilized in substantive domains due to lack of accessible diagnostic and software tools.
• Automation, Scalability, and Benchmarking: Systematic, scalable procedures for identification, estimation, inference, and validation are in urgent need, especially in the context of high-dimensional and complex data.

Implications and Directions for AI

The synergy between causal inference and recent advances in machine learning/AI systems is likely to reshape both fields. Causal reasoning, both as an object of automation and as a tool for trustworthy AI, is expected to be increasingly integrated with predictive and generative algorithms. Open interactions include: (1) causally regularized learning and automated policy optimization; (2) AI-facilitated representation learning for heterogeneity, mediation, and mechanistic discovery; (3) benchmarking and scalable sensitivity analysis under structural uncertainty; (4) data fusion and multi-source generalization.

Conclusion

The paper delineates causality and causal inference as a steadily maturing core domain of modern statistics, but one still typified by intricate, open technical questions—especially regarding robustness, heterogeneity, complex data, and automation. The path forward entails bridging statistical theory and empirical applications, pushing for systematic integration with modern computational and AI tools, and fostering an open, interdisciplinary research ecosystem. The field's future will hinge on progress toward adaptive, scalable, and interpretable causal strategies capable of coping with scientific and societal complexity.