DuPO: Enabling Reliable LLM Self-Verification via Dual Preference Optimization (2508.14460v1)

Abstract: We present DuPO, a dual learning-based preference optimization framework that generates annotation-free feedback via a generalized duality. DuPO addresses two key limitations: Reinforcement Learning with Verifiable Rewards (RLVR)'s reliance on costly labels and applicability restricted to verifiable tasks, and traditional dual learning's restriction to strictly dual task pairs (e.g., translation and back-translation). Specifically, DuPO decomposes a primal task's input into known and unknown components, then constructs its dual task to reconstruct the unknown part using the primal output and known information (e.g., reversing math solutions to recover hidden variables), broadening applicability to non-invertible tasks. The quality of this reconstruction serves as a self-supervised reward to optimize the primal task, synergizing with LLMs' ability to instantiate both tasks via a single model. Empirically, DuPO achieves substantial gains across diverse tasks: it enhances the average translation quality by 2.13 COMET over 756 directions, boosts the mathematical reasoning accuracy by an average of 6.4 points on three challenge benchmarks, and enhances performance by 9.3 points as an inference-time reranker (trading computation for accuracy). These results position DuPO as a scalable, general, and annotation-free paradigm for LLM optimization.

• The paper introduces a generalized duality framework that decomposes inputs into known and unknown components for reliable, annotation-free self-verification in LLMs.
• It employs dual-task construction in areas like mathematical reasoning and multilingual translation, demonstrating significant performance gains across various model sizes.
• Empirical results show improvements of 3.9–6.4 accuracy points and a +2.13 COMET boost, validating the effectiveness and scalability of the proposed method.

Dual Preference Optimization (DuPO): A Generalized Dual Learning Framework for Reliable LLM Self-Verification

Introduction and Motivation

The DuPO framework addresses a central challenge in LLM optimization: the need for scalable, annotation-free, and reliable self-verification signals. Existing reinforcement learning paradigms such as RLHF and RLVR are limited by their dependence on costly human annotations or the availability of verifiable ground-truth answers, restricting their applicability to a narrow set of tasks. Traditional dual learning, while promising for self-supervised feedback, is constrained by the requirement of strict task invertibility, which is rarely satisfied in real-world LLM applications such as mathematical reasoning or open-ended generation.

DuPO introduces a generalized duality framework that relaxes the invertibility constraint by decomposing the input into known and unknown components. The dual task is then defined as reconstructing the unknown component from the primal output and the known input, enabling the construction of reliable self-supervised rewards even for non-invertible tasks. This approach leverages the broad capabilities of LLMs to instantiate both primal and dual tasks within a single model, facilitating scalable and annotation-free preference optimization.

Generalized Duality: Theoretical Formulation

The core innovation of DuPO is the formalization of generalized duality. Let the input $\mathbf{x}$ be decomposed into known ($\mathbf{x}_k$) and unknown ($\mathbf{x}_u$) components. The primal task $\mathcal{T}_p$ maps $\mathbf{x}$ to output $\mathbf{y}$, while the complementary dual task $\mathcal{T}_{cd}$ reconstructs $\mathbf{x}_u$ from $(\mathbf{y}, \mathbf{x}_k)$. The self-supervised reward is defined as:

$$r(\mathbf{y}) \propto \exp\left(-\lambda \cdot d\left(\mathbf{x}_u, \mathcal{T}_{cd}(\mathbf{y}, \mathbf{x}_k)\right)\right)$$

where $d(\cdot)$ is a domain-specific distance metric and $\lambda$ controls reward sensitivity.

This formulation overcomes two critical limitations of classic dual learning:

1. Non-invertibility: By focusing on reconstructing only the unknown component, the framework is applicable to tasks where the output does not uniquely determine the input.
2. Competence Asymmetry: The dual task is simplified, as the known component constrains the solution space, reducing the risk of noisy or unreliable self-supervision.

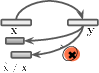
Figure 1: Challenges in dual learning for LLMs and the resolution via relaxed duality constraints, including non-unique reconstruction and competence asymmetry.

Practical Implementation and Task Instantiation

Mathematical Reasoning

In mathematical reasoning, DuPO constructs dual tasks by systematically masking numerical parameters in the problem statement and requiring the model to infer these values from the solution and the remaining context. For example, given a problem "A box contains 3 red and 5 blue balls; what is the total?", the dual task would be: "Given the total is 8 and there are 3 red balls, how many blue balls are there?" This approach ensures that the dual task is well-posed and that the reward signal is both informative and reliable.

Multilingual Translation

For translation, the dual task is instantiated as back-translation, but with the critical difference that only a subset of the input (e.g., specific semantic elements) is required to be reconstructed, rather than the entire sentence. This allows the framework to handle the inherent ambiguity and diversity of valid translations, which is a major limitation of RLVR and classic dual learning in open-ended tasks.

Training and Inference

DuPO is compatible with standard RL algorithms such as PPO and GRPO. During training, the model samples outputs for the primal task, computes the dual reconstruction, and uses the resulting reward to update the policy. At inference, DuPO can be used as a reranking mechanism: multiple candidate outputs are generated, and the one with the highest dual-task reward is selected, enabling performance gains without additional finetuning.

Empirical Results and Ablation Analysis

DuPO demonstrates substantial improvements across both mathematical reasoning and multilingual translation tasks. On translation, DuPO applied to Seed-X-7B-Instruct yields a +2.13 COMET improvement over 756 directions, matching or surpassing ultra-large models. In mathematical reasoning, DuPO consistently improves accuracy by 3.9–6.4 points across models from 1.5B to 7B parameters, with the Qwen3-4B model surpassing larger baselines.

Ablation studies confirm that the unknown component selection strategy is critical for stable optimization and noise reduction. Removing this mechanism leads to significant performance degradation, especially in smaller models.

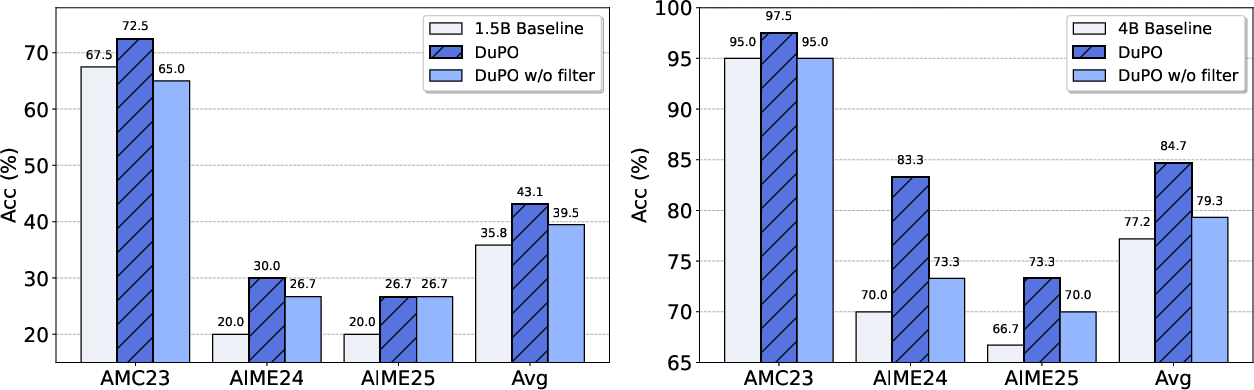
Figure 2: Ablation results showing the impact of unknown component selection on mathematical reasoning performance for DeepSeek-R1-Distill-Qwen-1.5B and Qwen3-4B.

Implications and Future Directions

DuPO's model-agnostic and annotation-free design positions it as a scalable solution for LLM optimization across diverse domains. The framework's ability to generate reliable self-supervised rewards without external labels or handcrafted rules addresses a major bottleneck in LLM development. The dual-task construction is flexible and can be adapted to a wide range of tasks, including code generation, dialogue, and potentially open-ended instruction following.

However, the computational overhead of unknown component selection and dual task construction, especially in mathematical reasoning, remains a practical limitation. Further research into efficient or learnable selection mechanisms is warranted. Additionally, while DuPO demonstrates strong results on moderate-scale models, its scalability to ultra-large models and more open-ended tasks requires further empirical validation.

Conclusion

DuPO advances the state of LLM self-verification by introducing a generalized duality framework that enables reliable, annotation-free preference optimization. By decomposing tasks into known and unknown components and leveraging complementary dual tasks, DuPO overcomes the limitations of classic dual learning and RL-based methods. Empirical results across translation and reasoning tasks validate its effectiveness and robustness. The framework's flexibility and scalability suggest broad applicability, with future work needed to address computational efficiency and extend to more complex, open-ended domains.