Learning without training: The implicit dynamics of in-context learning (2507.16003v1)

Abstract: One of the most striking features of LLMs (LLM) is their ability to learn in context. Namely at inference time an LLM is able to learn new patterns without any additional weight update when these patterns are presented in the form of examples in the prompt, even if these patterns were not seen during training. The mechanisms through which this can happen are still largely unknown. In this work, we show that the stacking of a self-attention layer with an MLP, allows the transformer block to implicitly modify the weights of the MLP layer according to the context. We argue through theory and experimentation that this simple mechanism may be the reason why LLMs can learn in context and not only during training. Specifically, we show under mild simplifying assumptions how a transformer block implicitly transforms a context into a low-rank weight-update of the MLP layer.

• The paper demonstrates that a transformer block implicitly updates MLP weights via context, forming a 'contextual block' with rank-1 weight modifications.
• The methodology links in-context learning to a process analogous to online gradient descent, verified through experiments on learning linear functions.
• Empirical results show that MLP weight updates converge with increased context, aligning the implicit learning dynamics with traditional fine-tuning processes.

Implicit Learning Dynamics in LLMs

This paper (2507.16003) addresses the phenomenon of in-context learning (ICL) in LLMs, where the model adapts to new patterns presented in the prompt without explicit weight updates. The authors propose that the combination of a self-attention layer and an MLP allows the transformer block to implicitly modify the weights of the MLP layer based on the context. They argue that this mechanism enables LLMs to learn in context, providing theoretical support and experimental validation for this claim. The paper introduces the concept of a "contextual block" as a generalization of a transformer block and demonstrates how it transforms context into a low-rank weight update of the MLP layer.

Contextual Blocks and Implicit Weight Updates

The paper introduces the notion of a contextual block, generalizing the transformer block architecture. A contextual block comprises a contextual layer stacked with a neural network. The contextual layer, denoted as $A(\cdot)$, can take a single vector $x$ as input, yielding an output $A(x)$, or it can take a context $C$ along with the vector $x$, yielding $A([C, x])$. The authors show that for contextual blocks, a token output in the presence of a context coincides with the neural network output for that token without context but with its weight matrix updated by a low-rank matrix.

The central theorem demonstrates that a contextual block transforms a portion $Y$ of a context $C$ into an implicit update of the neural network weights, such that the weight matrix $W$ becomes $W + \Delta W(Y)$. The formula for this update is:

$$\Delta W(Y) = \frac{(W \Delta A(Y)) A(C\backslash Y, x)^T}{\|A(C\backslash Y, x)\|^2}$$

where $\Delta A(Y) = A(C,x) - A(C\backslash Y, x)$. The authors emphasize that $\Delta W(Y)$ is a rank 1 matrix, suggesting that contextual layers perform an implicit fine-tuning of the MLP weights based on the context.

Implicit Learning Dynamics and Gradient Descent

The paper further explores the implicit learning dynamics of ICL by considering the context $C=[c_1, \dots, c_n]$ as a sequence of tokens. By iteratively applying the theorem, the authors uncover a learning dynamic where each context token incrementally updates the weights. This leads to a sequence of context weights $W_1, W_2, \dots, W_n$ that converge to the effect of the full context on the MLP weight. The authors demonstrate that this implicit learning dynamic resembles online gradient descent, where tokens act as data points, and the loss function changes at each step depending on the considered token.

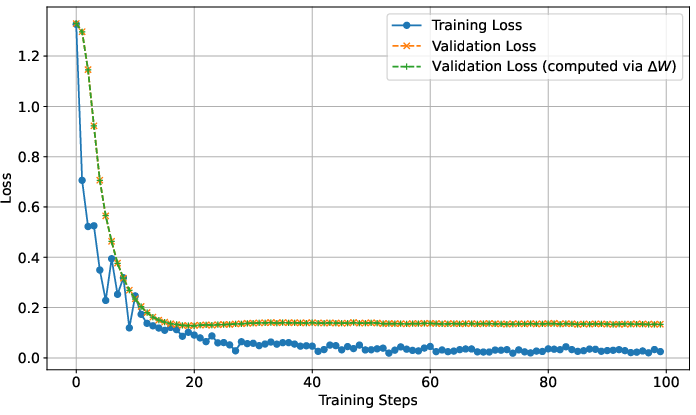
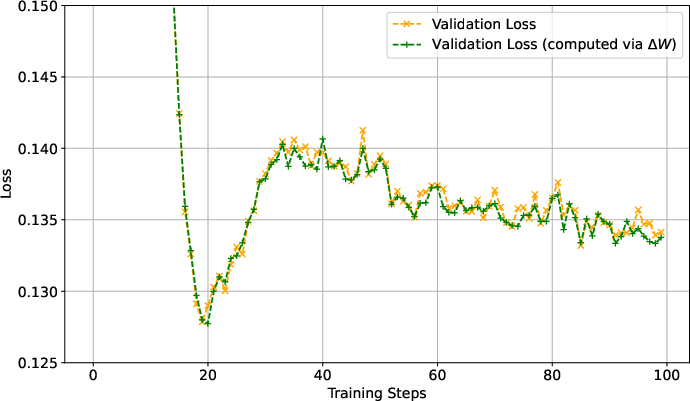
Figure 1: Train and Validation loss curves. Here, the "Validation loss (computed via $\Delta W$)" refers the loss computed using $T_{W + \Delta W}(x)$; i.e., the trained model prediction given only $x_{query}$ but with MLP weights modified by $\Delta W$ as defined in Equation (1).

Proposition 1 formalizes this connection by expressing the iterative weight updates as stochastic gradient updates:

$W_i = W_{i-1} - h \nabla_W L_i(W_{i-1})$

where the learning rate $h = 1/\|A(x)\|^2$ and the loss at step $i$ is $L_i(W) = \operatorname{trace}(\Delta_i^T W)$, with $\Delta_i$ measuring the effect of adding context token $c_{i+1}$ to the partial context $c_1,\dots, c_i$.

Experimental Verification

The authors conduct experiments to verify their theoretical results, focusing on the task of learning linear functions in context. They train a transformer model on instances of prompts consisting of input-output pairs $(x_1, h(x_1), \dots, x_N, h(x_N), x_{\query})$, where $h$ is a linear function. The experiments demonstrate that the in-context prompt can be effectively transferred to a weight update, as defined in the main theorem. Specifically, the prediction made by the trained model with an in-context prompt is shown to be nearly identical to the prediction made by the model with MLP weights modified according to the derived formula, but without access to the in-context prompt. This provides strong empirical support for the theoretical framework.

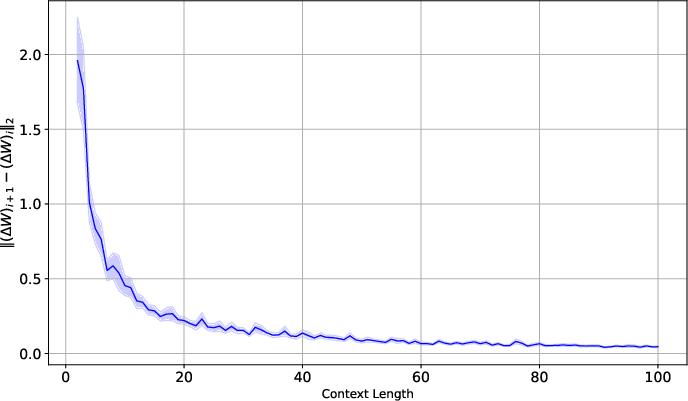
Figure 2: Convergence of $(\Delta W)_i$. As more of the context in processed, the relative change in the weights $W$ converges to zero. For context length $i>2$, the plot above represents the average difference $\|(\Delta W)_{i+1} - (\Delta W)_{i}\|_2$ and the standard error over 100 separate trials.

The convergence of the weight updates is also investigated. The experiments confirm that as the model processes more of the prompt, the relative change in the weight updates decreases, indicating a convergence towards a stable solution. This behavior aligns with the expected behavior of a converging gradient descent process.

Comparison with Fine-tuning

The paper compares the implicit weight-update dynamics with explicit fine-tuning. A transformer model is pretrained and then fine-tuned using stochastic gradient descent. The fine-tuning process is compared to the $\Delta W$ weight transfer test loss. The results indicate that while different, both learning processes minimize the loss in similar ways.

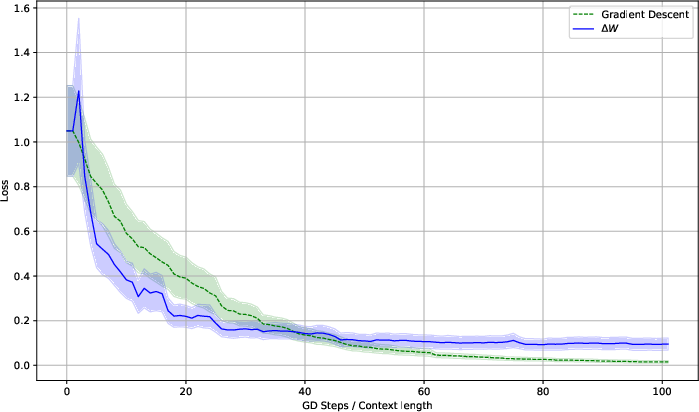
Figure 3: N/A

Conclusion

The authors provide a theoretical framework and experimental evidence suggesting that ICL can be understood as an implicit weight update process within the MLP layer of a transformer block. This perspective shifts the focus from the self-attention mechanism to the ability of neural networks to transfer modifications of the input space to their weight structure. While the analysis is limited to a single transformer block and the first generated token, it offers valuable insights into the mechanisms underlying ICL. Future research could focus on extending this framework to multi-layer transformers and exploring the implications for the generative capabilities of LLMs.