LoRA: Low-Rank Adaptation of Large Language Models
Abstract: An important paradigm of natural language processing consists of large-scale pre-training on general domain data and adaptation to particular tasks or domains. As we pre-train larger models, full fine-tuning, which retrains all model parameters, becomes less feasible. Using GPT-3 175B as an example -- deploying independent instances of fine-tuned models, each with 175B parameters, is prohibitively expensive. We propose Low-Rank Adaptation, or LoRA, which freezes the pre-trained model weights and injects trainable rank decomposition matrices into each layer of the Transformer architecture, greatly reducing the number of trainable parameters for downstream tasks. Compared to GPT-3 175B fine-tuned with Adam, LoRA can reduce the number of trainable parameters by 10,000 times and the GPU memory requirement by 3 times. LoRA performs on-par or better than fine-tuning in model quality on RoBERTa, DeBERTa, GPT-2, and GPT-3, despite having fewer trainable parameters, a higher training throughput, and, unlike adapters, no additional inference latency. We also provide an empirical investigation into rank-deficiency in LLM adaptation, which sheds light on the efficacy of LoRA. We release a package that facilitates the integration of LoRA with PyTorch models and provide our implementations and model checkpoints for RoBERTa, DeBERTa, and GPT-2 at https://github.com/microsoft/LoRA.
Paper Prompts
Sign up for free to create and run prompts on this paper using GPT-5.
Top Community Prompts
Explain it Like I'm 14
Overview
This paper introduces a simple, smart way to customize very LLMs (like GPT-3) for new tasks without retraining the whole model. The method is called LoRA, which stands for Low-Rank Adaptation. The big idea: instead of changing all the model’s billions of settings (“parameters”), you keep the original model frozen and only train a few small add-on pieces that gently nudge it toward the new task.
Key Objectives
The paper set out to answer three plain questions:
- How can we adapt huge LLMs to new tasks without needing massive computer power and storage?
- Can a small number of changes be enough to make a big model work well on lots of different tasks?
- Will this approach be fast at runtime and still match or beat the usual full fine-tuning in quality?
How LoRA Works (Simple Explanation)
Think of a giant, high-end camera that’s already trained to take great photos in many conditions. Full fine-tuning is like opening the camera and reconfiguring every internal part for each new type of shot—slow, risky, and expensive. LoRA is like clipping on a tiny lens filter to adjust the picture for your new scene. You don’t change the camera; you just add a lightweight attachment.
Here’s the everyday version of the technical idea:
- A Transformer (the type of model used in GPT) has many “weight matrices”—big grids of numbers that transform inputs into outputs.
- Full fine-tuning updates all those big grids, which is costly for huge models.
- LoRA freezes the original big grids and adds two small helper matrices, called A and B, per chosen layer. When you multiply B and A, you get a tiny “change matrix” that gently adjusts the original weights.
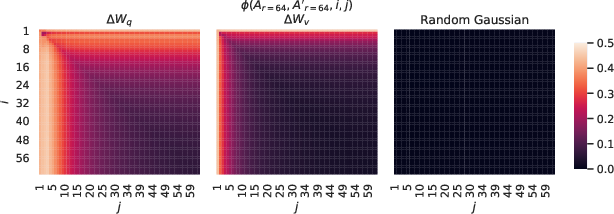
- This “low-rank” change means the adjustment is limited to a few “directions,” like moving a little bit north-east instead of exploring every possible direction. “Rank” is just the number of those directions; a small rank (like 1–4) can still do a lot.
Practical details:
- The paper mostly applies LoRA to the attention parts of Transformers (often the query and value projection matrices, named Wq and Wv), because they matter a lot for how the model focuses on different words.
- The original weights stay frozen; only the little A and B matrices are trained.
- At deployment time, you can combine the small changes with the original weights so the model runs as fast as usual—no extra delay.
Main Findings and Why They Matter
Here are the most important takeaways put simply:
- Much fewer trainable parameters: LoRA can reduce the number of trainable parameters by up to 10,000 times compared to full fine-tuning on GPT-3. That’s like swapping a full toolbox for a couple of tiny tools that still get the job done.
- Lower memory and faster training: Because you’re only training the small A and B pieces, training uses around 3× less GPU memory and often runs faster. This lowers costs and makes customization more accessible.
- No extra runtime delay: Unlike some other methods (like “adapters”) that add extra steps when the model runs, LoRA adds no extra latency. You can merge the changes so the model behaves like a fully fine-tuned one.
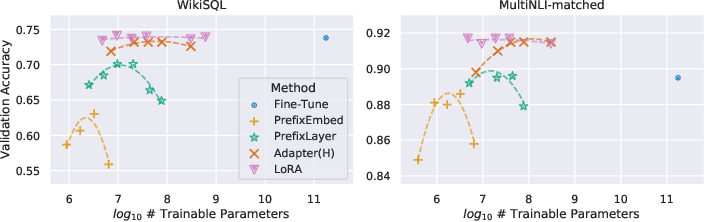
- Performance matches or beats full fine-tuning: Across many models and tasks—RoBERTa, DeBERTa, GPT-2, and even huge GPT-3—LoRA often matches or outperforms full fine-tuning and other parameter-efficient techniques (like adapters or prompt/prefix tuning).
- Very small ranks work: Surprisingly, even tiny ranks (like r=1 or r=2) were enough for good results in several tasks. This suggests that the specific changes needed to adapt a LLM are often simple and lie in just a few “directions.”
- Best layers to adapt: Adapting the attention projections for queries and values (Wq and Wv) together tended to give strong results for the same parameter budget.
The paper backs these claims with experiments on:
- Understanding tasks (GLUE benchmark) using RoBERTa and DeBERTa.
- Generation tasks using GPT-2 (like the E2E NLG Challenge).
- Big tasks using GPT-3 (WikiSQL for SQL generation, MNLI for natural language inference, SAMSum for conversation summarization).
Implications and Impact
In plain terms, LoRA makes it much easier to personalize giant LLMs for many different uses:
- Companies can keep one big base model and swap tiny LoRA “modules” for different tasks, saving storage and making updates faster.
- Developers with fewer resources can still adapt top models, opening the door to more innovation and fair access.
- Because LoRA doesn’t slow down the model when it runs, it’s suitable for real-world apps that care about quick responses.
- LoRA can be combined with other techniques, giving even more flexibility.
Overall, LoRA shows that you don’t need to overhaul a massive model to make it great at new tasks—smart, small adjustments can be enough. This could speed up progress in language AI while keeping costs and energy use in check.
Collections
Sign up for free to add this paper to one or more collections.