Heterosynaptic Circuits Are Universal Gradient Machines (2505.02248v1)

Abstract: We propose a design principle for the learning circuits of the biological brain. The principle states that almost any dendritic weights updated via heterosynaptic plasticity can implement a generalized and efficient class of gradient-based meta-learning. The theory suggests that a broad class of biologically plausible learning algorithms, together with the standard machine learning optimizers, can be grounded in heterosynaptic circuit motifs. This principle suggests that the phenomenology of (anti-) Hebbian (HBP) and heterosynaptic plasticity (HSP) may emerge from the same underlying dynamics, thus providing a unifying explanation. It also suggests an alternative perspective of neuroplasticity, where HSP is promoted to the primary learning and memory mechanism, and HBP is an emergent byproduct. We present simulations that show that (a) HSP can explain the metaplasticity of neurons, (b) HSP can explain the flexibility of the biology circuits, and (c) gradient learning can arise quickly from simple evolutionary dynamics that do not compute any explicit gradient. While our primary focus is on biology, the principle also implies a new approach to designing AI training algorithms and physically learnable AI hardware. Conceptually, our result demonstrates that contrary to the common belief, gradient computation may be extremely easy and common in nature.

• The paper introduces heterosynaptic circuits as a basis for gradient-based meta-learning that unifies biological plasticity with machine learning.
• Simulations demonstrate that heterosynaptic stability and dynamical consistency enable robust learning even with sparse or random connectivity.
• The findings challenge conventional Hebbian paradigms and open new avenues for analog AI hardware and evolutionary model designs.

Heterosynaptic Circuits Are Universal Gradient Machines

The paper "Heterosynaptic Circuits Are Universal Gradient Machines" (arXiv ID: (2505.02248)) proposes a novel design principle for understanding learning processes in the biological brain through heterosynaptic plasticity. This principle suggests that almost any dendritic weights updated via heterosynaptic plasticity can implement a generalized form of efficient gradient-based meta-learning, bridging biological learning with standard machine learning optimizers. The findings challenge the traditional Hebbian learning paradigm and promote heterosynaptic plasticity as the primary mechanism for learning and memory, with Hebbian plasticity being an emergent byproduct.

Theoretical Framework and Principles

The principle hinges on two key concepts: heterosynaptic stability (HS) and dynamical consistency (DC). HS implies that when synapse weights for one signal reach stability, local emergent properties govern the learning dynamics. These local patches are characterized by a scalar "consistency score," $\phi$, ensuring synchronized learning across the network (Figure 1).

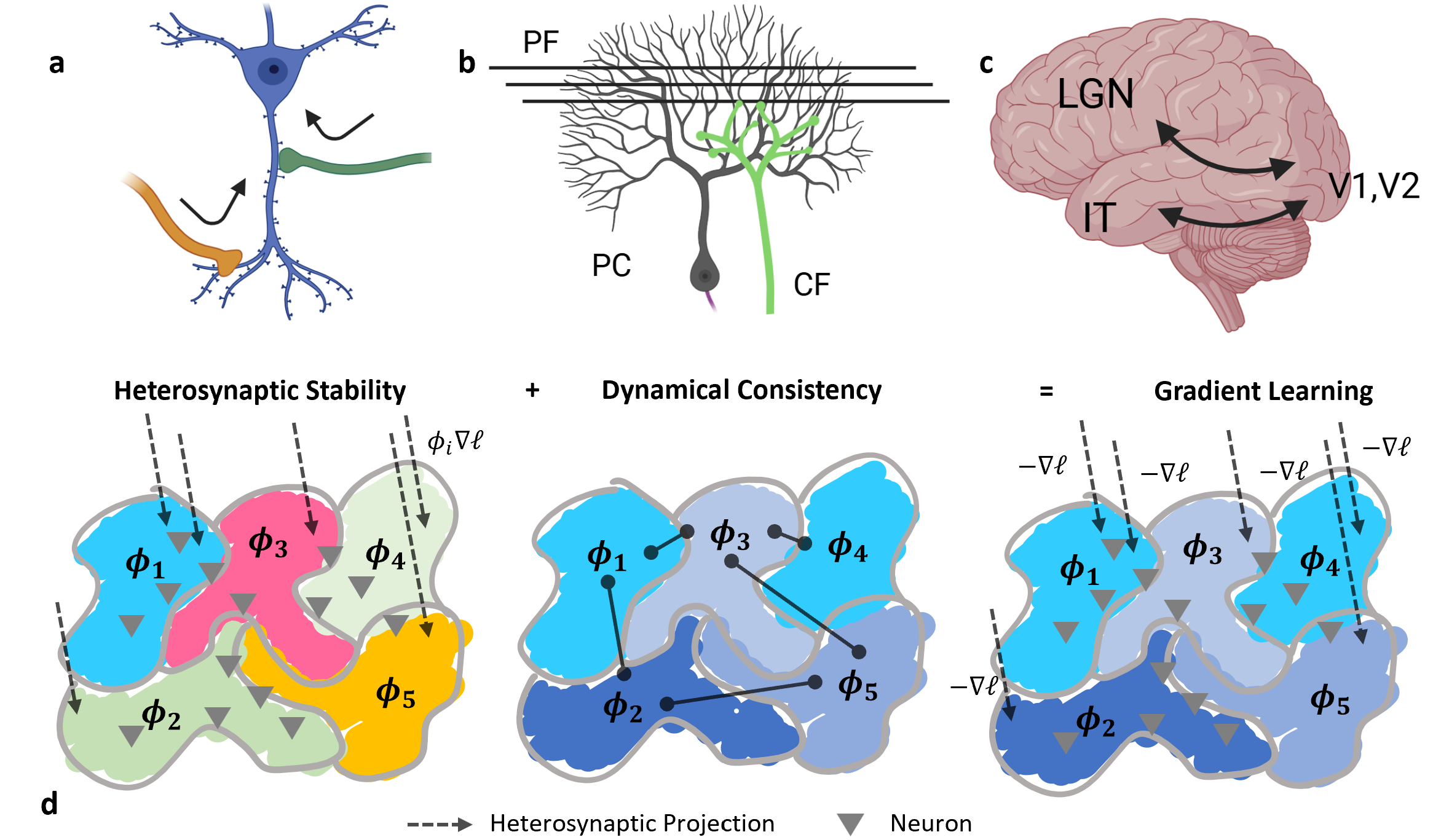
Figure 1: Structures of heterosynaptic circuits across scales, with HS and DC enabling gradient learning characterized by a scalar consistency score $\phi$.

DC, on the other hand, ensures that these scores are consistent across patches, leading to universal gradient learning without the need for explicit computation of gradients. This creates a robust and flexible learning system applicable to various network architectures, resembling topologies observed in biological systems.

Simulation and Emergence

Simulation experiments demonstrate the capability of heterosynaptic circuits to support gradient learning through simple evolutionary dynamics, even when network connectivity is initially random or sparse (Figure 2).

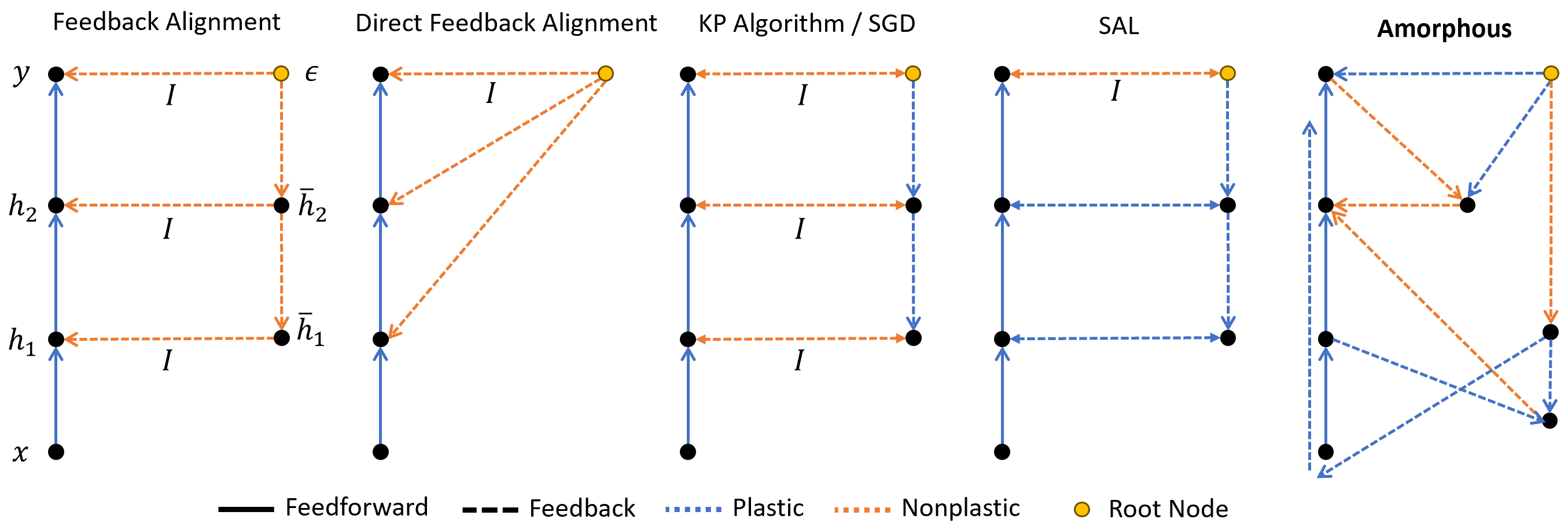
Figure 2: Training a neural network using heterosynaptic circuits showcases potential learning dynamics similar to known feedback alignment methods.

These simulations illustrate how neurons can achieve metaplasticity—where prior experiences influence current learning rates—and how gradient learning can emerge quickly from simple, non-gradient-based evolutionary changes.

Heterosynaptic Stability and Flexibility

HS plays a critical role in enabling meta-gradient learning by positing that a neuron can respond predictably to incoming signals only when its synapses exhibit stability. Stability is often synonymous with homeostasis in neuron plasticity literature, addressing both stability and robustness requirements. Simulations using non-differentiable activations (e.g., step-ReLU) show that learning is robust against activation imperfections, a characteristic absent in typical SGD methods (Figures 3 and 4).

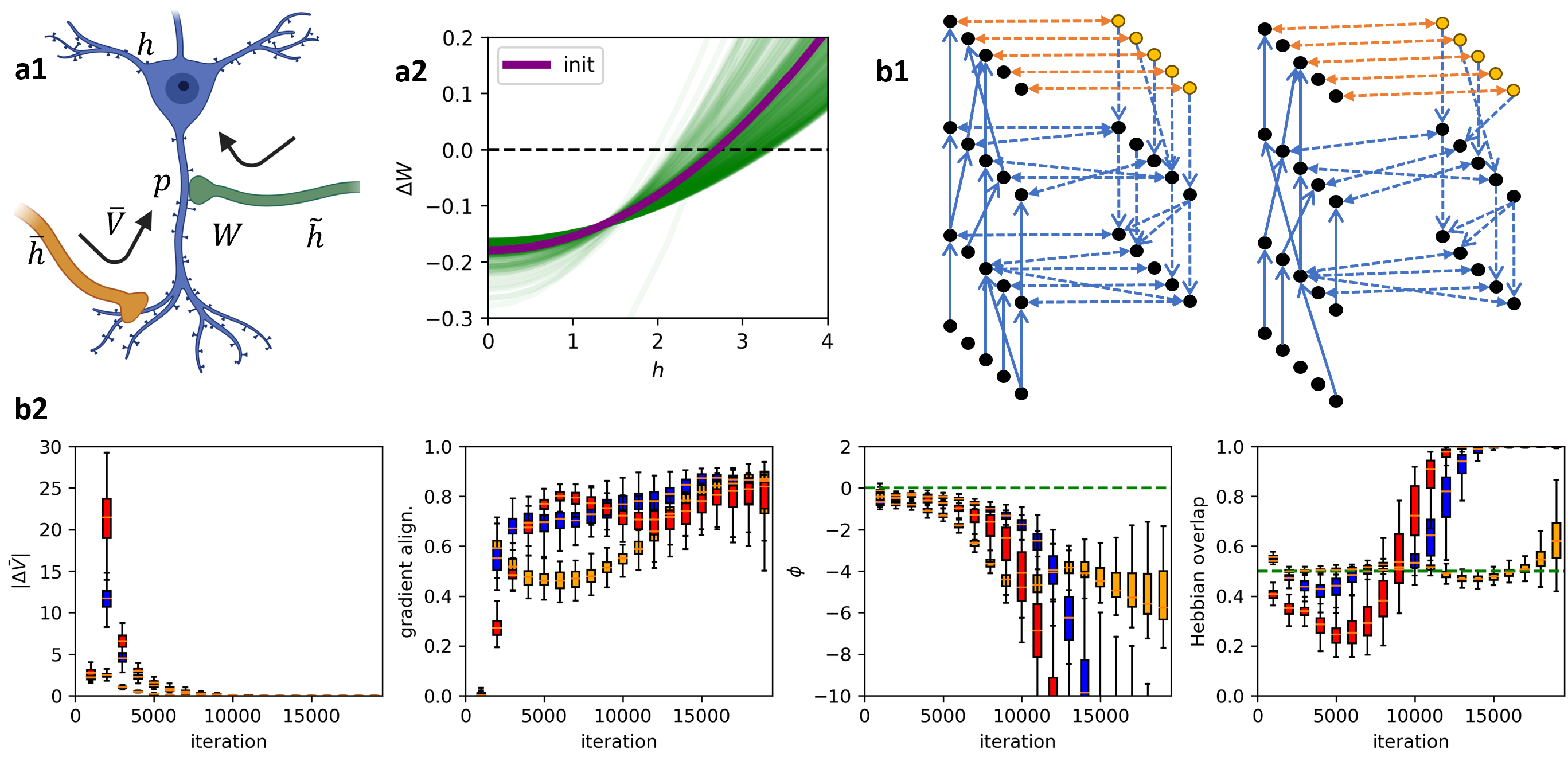
Figure 3: Meta-plasticity characterizing neuron learning in micro connectivity networks, indicating adaptable learning capabilities.

Altered Perspectives on Neuroplasticity

The paper presents a paradigm shift, suggesting heterosynaptic plasticity as the main driver of learning, with Hebbian dynamics derived as secondary outcomes. This perspective prevents divergence issues typically associated with Hebbian learning and eliminates the need for separate stabilizing mechanisms, offering a simpler, resource-efficient model.

Practical Applications and Future Directions

These insights pave the way for new directions in AI training algorithm design and AI hardware development. By leveraging heterosynaptic circuits, AI algorithms can avoid explicit gradient computations, thus becoming conducive to implementation in analog AI systems like photonic and quantum computers. The research suggests optimizing feedback connections in neural networks to potentially enhance learning efficiency by embedding feedback mechanisms into the network architecture itself.

The potential of evolutionary growth enabling better-performing circuits highlights practical pathways for AI system design, essentially allowing for improved performance through incremental biologically-inspired architectural evolutions (Figure 4).

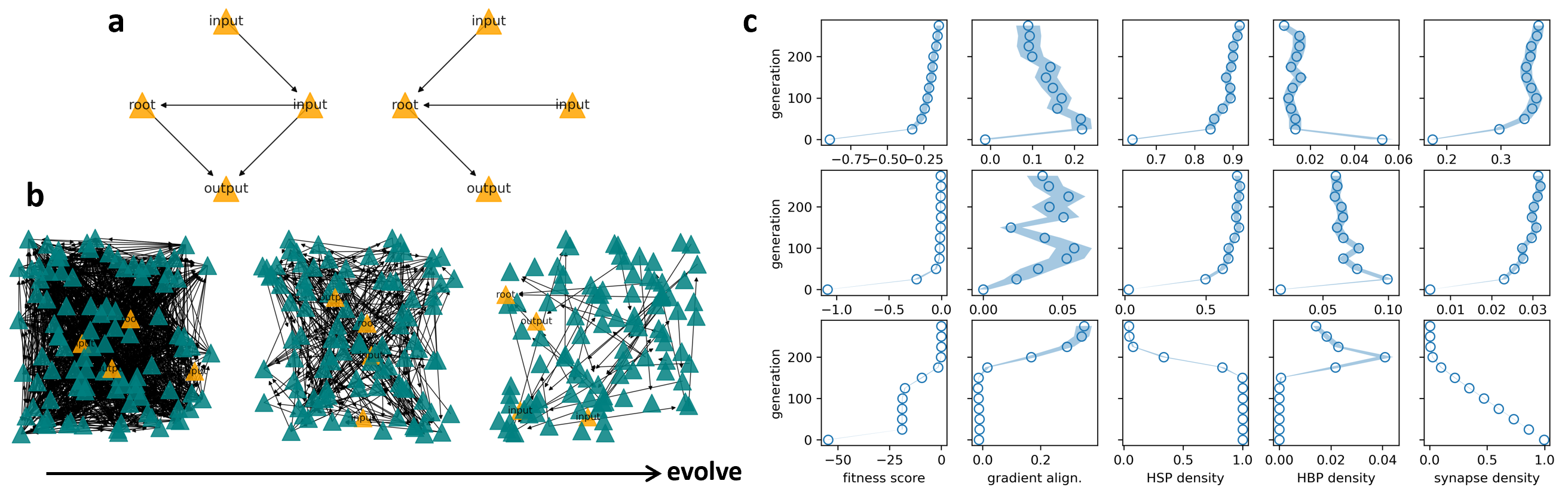
Figure 4: Evolution of circuits showing improved alignment with gradient-based methods, highlighting the role of evolutionary dynamics in optimization.

Conclusion

The proposed theory harmonizes biological plausibility with computational efficiency and flexibility, offering a unified explanation for diverse plasticity mechanisms observed in nature. Its implications resonate with the advancement of AI systems design, suggesting novel methods for optimizer architecture construction and analog hardware implementations. Future research may focus on delineating second-order effects, expanding on neuroplasticity's role in complex learning systems, and exploring more sophisticated connectivity structures within networks.