Emergence of Hebbian Dynamics in Regularized Non-Local Learners (2505.18069v1)

Abstract: Stochastic Gradient Descent (SGD) has emerged as a remarkably effective learning algorithm, underpinning nearly all state-of-the-art machine learning models, from LLMs to autonomous vehicles. Despite its practical success, SGD appears fundamentally distinct from biological learning mechanisms. It is widely believed that the biological brain can not implement gradient descent because it is nonlocal, and we have found little (if any) experimental evidence for it. In contrast, the brain is widely thought to learn via local Hebbian learning principles, which have been seen as incompatible with gradient descent. In this paper, we establish a theoretical and empirical connection between the learning signals of neural networks trained using SGD with weight decay and those trained with Hebbian learning near convergence. We show that SGD with regularization can appear to learn according to a Hebbian rule, and SGD with injected noise according to an anti-Hebbian rule. We also provide empirical evidence that Hebbian learning properties can emerge in a network with weight decay from virtually any learning rule--even random ones. These results may bridge a long-standing gap between artificial and biological learning, revealing Hebbian properties as an epiphenomenon of deeper optimization principles and cautioning against interpreting their presence in neural data as evidence against more complex hetero-synaptic mechanisms.

• The paper establishes a theoretical and empirical link between SGD with weight decay and the emergence of Hebbian dynamics near convergence.
• It demonstrates that strong regularization and noise induce a transition between Hebbian and anti-Hebbian updates across various architectures.
• The study highlights transient phases where a balance between expansion and contraction forces optimizes network generalization.

Emergence of Hebbian Dynamics in Regularized Non-Local Learners

Introduction

Hebbian and anti-Hebbian plasticity are commonly observed in biological neural networks, traditionally considered distinct from artificial learning mechanisms such as Stochastic Gradient Descent (SGD). This paper establishes a theoretical and empirical connection between SGD with regularization in artificial neural networks and Hebbian-like learning dynamics near convergence. It suggests that Hebbian and anti-Hebbian properties can emerge from deeper optimization principles rather than being distinct learning phenomena, cautioning against misinterpreting their presence as evidence against complex heterosynaptic mechanisms.

Learning-Regularization Balance and Hebbian Learning

The paper reveals that near stationarity, almost any learning rule—including SGD with weight decay—can appear Hebbian. When the weight decay is strong enough, SGD dynamics show a monotonic increase in alignment with Hebbian learning principles. This suggests that any algorithm with weight decay might mimic Hebbian dynamics, thus implying a universal property of gradient-based optimization meeting certain regularization criteria.

Figure 1: Close to the end of learning, the contraction forces must balance with the expansion forces for deep learning and biology, affecting the gradient's alignment with Hebbian or anti-Hebbian rules.

Empirical investigations further support the universality of this phenomenon across various models and tasks, demonstrating that correlations between SGD updates and Hebbian updates amplify with increasing weight decay. The experiments across different architectures, activation functions, and learning rules substantiate these findings, suggesting potential implications for understanding biological learning systems.

Learning-Noise Balance and Anti-Hebbian Learning

This paper also addresses scenarios under which anti-Hebbian learning emerges, focusing on environments with high noise levels. It illustrates that noise effectively leads to anti-Hebbian dynamics when expansion dominates over contraction. The relationship outlined shows a clear phase transition boundary at $\gamma \propto \sigma^2$ between Hebbian and anti-Hebbian alignment, confirmed by experimental data.

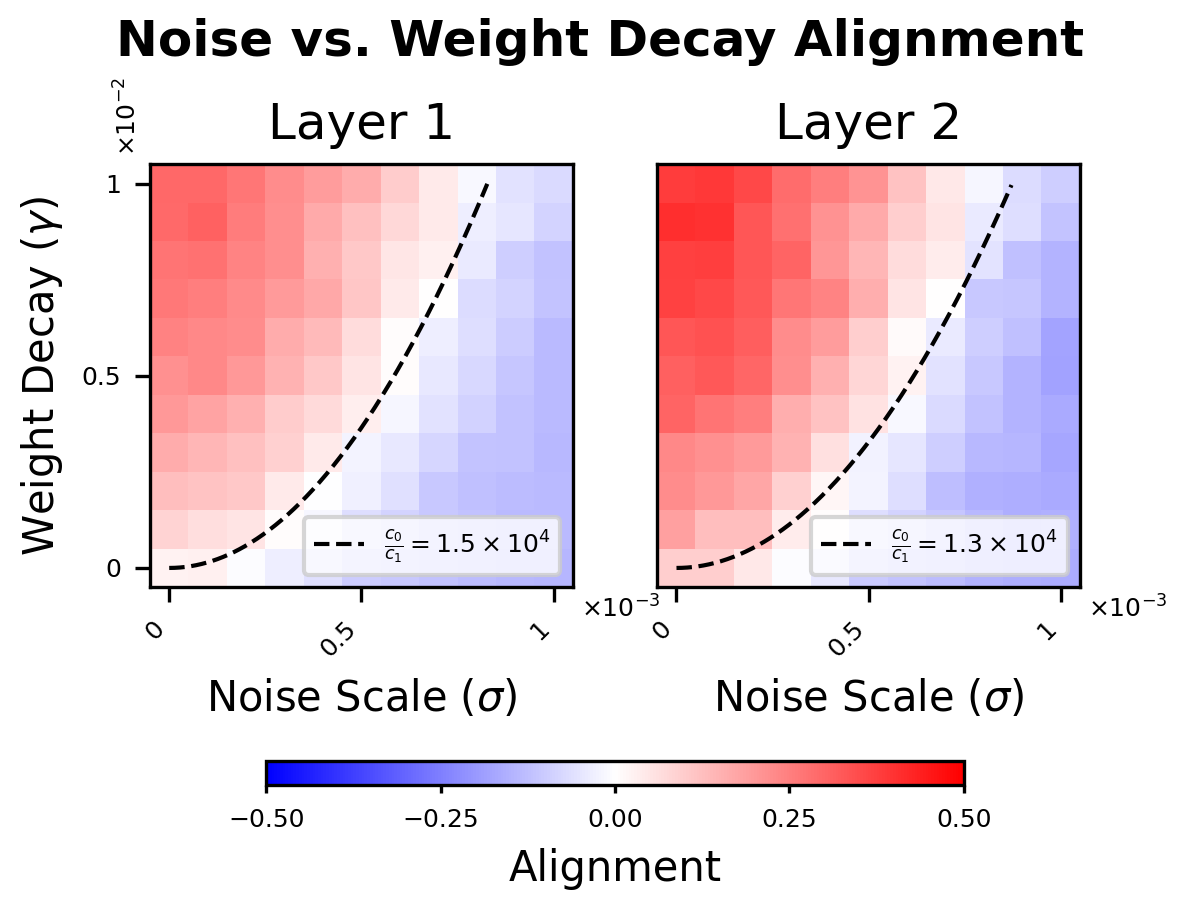
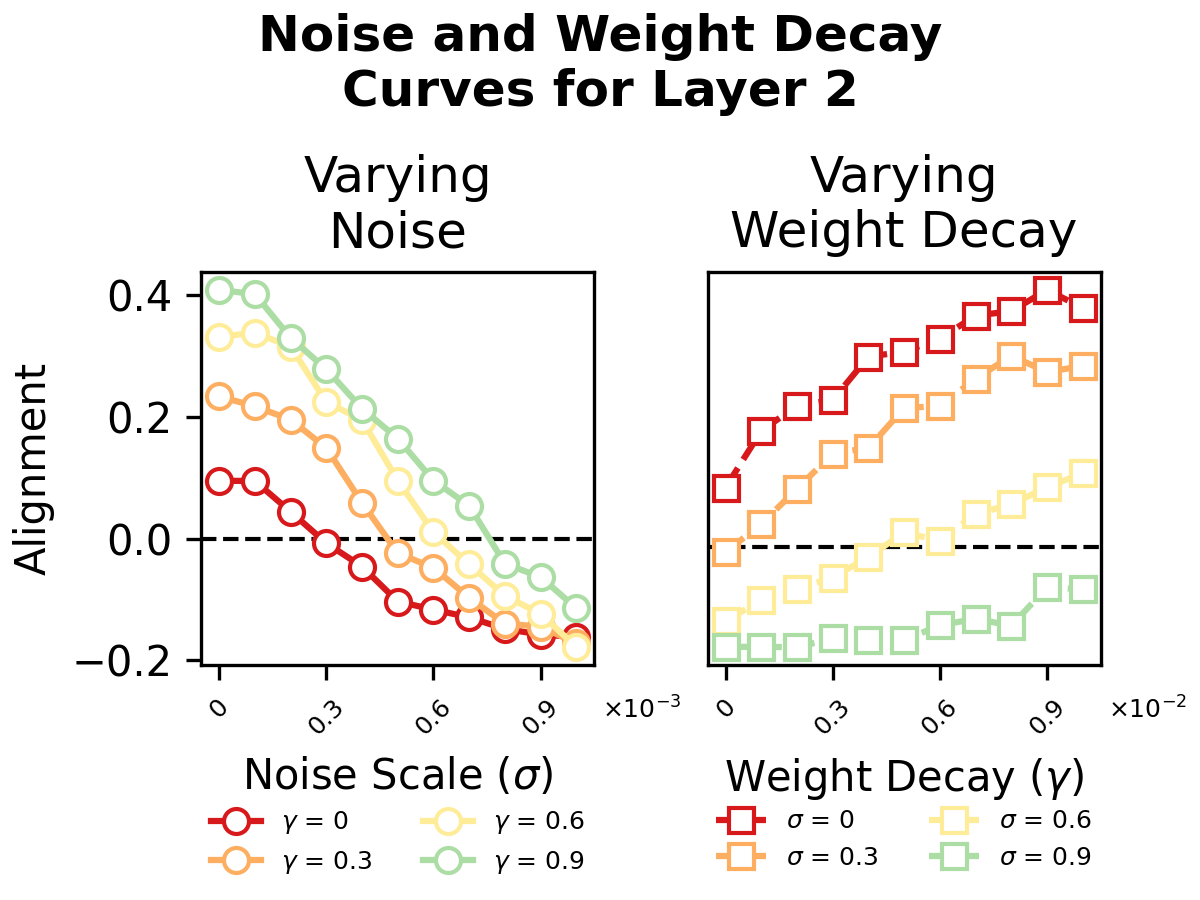
Figure 2: Hebbian alignment decreases with increasing noise, illustrating a quadratic phase boundary between Hebbian and anti-Hebbian dynamics with varied weight decays.

The paper's simulations reveal that strong noise contexts push gradient updates into anti-Hebbian territories, thereby imitating biologically plausible anti-Hebbian learning processes. However, surprisingly, the model's optimal performance is reached when neither Hebbian nor anti-Hebbian learning dominates, emphasizing the role of balance for effective generalization.

Transient Phases During Training

The paper identifies intriguing learning dynamics beyond steady-state phenomena, highlighting transient phases where neurons rapidly switch between Hebbian and anti-Hebbian roles. Initial training often sees a surge in Hebbian-aligned updates, with steady-state training oscillations demonstrating a balance crucial for model stabilization and consistency.

Figure 3: Distinct initial jump in Hebbian alignment during training with low learning rates observed; effect size varies with initial conditions.

During these phases, the alignment can switch depending on weight initialization, decay parameters, and training configurations. These observations open discussions on interpreting neuro-physiological data where similar transient dynamics may reflect complex underlying optimization rather than strict local learning rules.

Discussion

The implications of these findings are multifold—suggesting Hebbian and anti-Hebbian dynamics as emergent properties of optimization processes guided by regularization and noise. This work challenges the traditional view separating Hebbian updates from SGD, proposing that observed neuro-physiological plasticity patterns might inherently arise from global optimization principles rather than localized rules alone.

The results foster practical machine learning methodologies by monitoring alignment trends for regularization tuning. Additionally, they advocate for reevaluating experimental evidence in neuroscience, encouraging exploration of heterosynaptic circuits as integral components in memory and learning beside Hebbian plasticity. Future research could explore larger models and deeper network layers to refine understanding of transient dynamics, potentially revealing further insights into complex learning processes mirroring biological systems.

Concluding, this investigation provides a theoretical framework and empirical validation that bridges a gap between artificial and biological learning by illustrating emergent Hebbian-like behavior in deep learning architectures training under regularization and noise.