Trajectory Planning with Model Predictive Control for Obstacle Avoidance Considering Prediction Uncertainty (2504.19193v1)

Abstract: This paper introduces a novel trajectory planner for autonomous robots, specifically designed to enhance navigation by incorporating dynamic obstacle avoidance within the Robot Operating System 2 (ROS2) and Navigation 2 (Nav2) framework. The proposed method utilizes Model Predictive Control (MPC) with a focus on handling the uncertainties associated with the movement prediction of dynamic obstacles. Unlike existing Nav2 trajectory planners which primarily deal with static obstacles or react to the current position of dynamic obstacles, this planner predicts future obstacle positions using a stochastic Vector Auto-Regressive Model (VAR). The obstacles' future positions are represented by probability distributions, and collision avoidance is achieved through constraints based on the Mahalanobis distance, ensuring the robot avoids regions where obstacles are likely to be. This approach considers the robot's kinodynamic constraints, enabling it to track a reference path while adapting to real-time changes in the environment. The paper details the implementation, including obstacle prediction, tracking, and the construction of feasible sets for MPC. Simulation results in a Gazebo environment demonstrate the effectiveness of this method in scenarios where robots must navigate around each other, showing improved collision avoidance capabilities.

• The paper introduces an MPC-based trajectory planner that utilizes VAR models to predict dynamic obstacle positions and avoid collisions.
• It employs probabilistic constraints based on Mahalanobis distance to construct safe trajectory regions while meeting kinodynamic limits.
• Simulation results in Gazebo demonstrate effective collision avoidance and acceptable real-time performance under dynamic conditions.

Trajectory Planning with Model Predictive Control (MPC) for Obstacle Avoidance Considering Prediction Uncertainty

Introduction

The paper presents a trajectory planner aimed at enhancing autonomous robot navigation through dynamic obstacle avoidance, integrated within the Robot Operating System 2 (ROS2) framework. Unlike conventional Nav2 trajectory planners which cater predominantly to static obstacles, this planner utilizes Model Predictive Control (MPC) to predict future positions of dynamic obstacles, employing a stochastic Vector Auto-Regressive Model (VAR). By representing obstacle positions as probability distributions and incorporating constraints based on the Mahalanobis distance, the planner ensures robots navigate regions with minimal likelihood of collision while adhering to kinodynamic constraints.

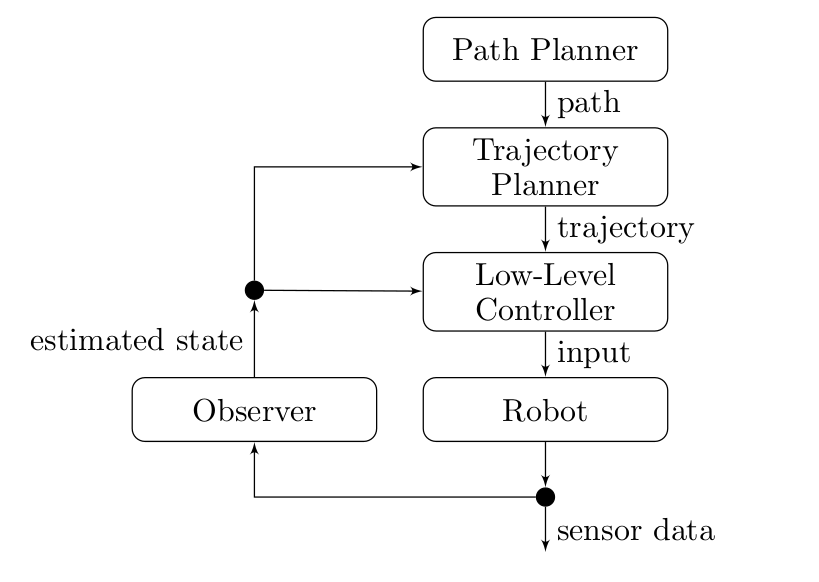
Figure 1: Overview: Control Structure

Methodology

Model Predictive Control Framework

The MPC framework is structured around a discrete-time dynamical model for robots, focusing on trajectory optimization over a prediction horizon. The paper defines the MPC problem as a non-convex optimization challenge, accommodating state and input constraints while emphasizing dynamic obstacle avoidance within the robot's workspace. Dynamic obstacles are characterized by probability distributions, and collision avoidance is managed through set construction that includes both static and dynamic obstacle sets.

Set Construction

Dynamic obstacles are modeled with position distributions $\mathcal{N}(\mu, \Sigma)$, where Mahalanobis distance determines probabilistic constraints for collision avoidance. The ellipse constructed from these constraints represents the feasible regions, augmented by robot and obstacle radii to ensure safety margins. This approach leverages coordinate transformations and eigen-decomposition to scale and orient ellipses efficiently within the prediction horizon.

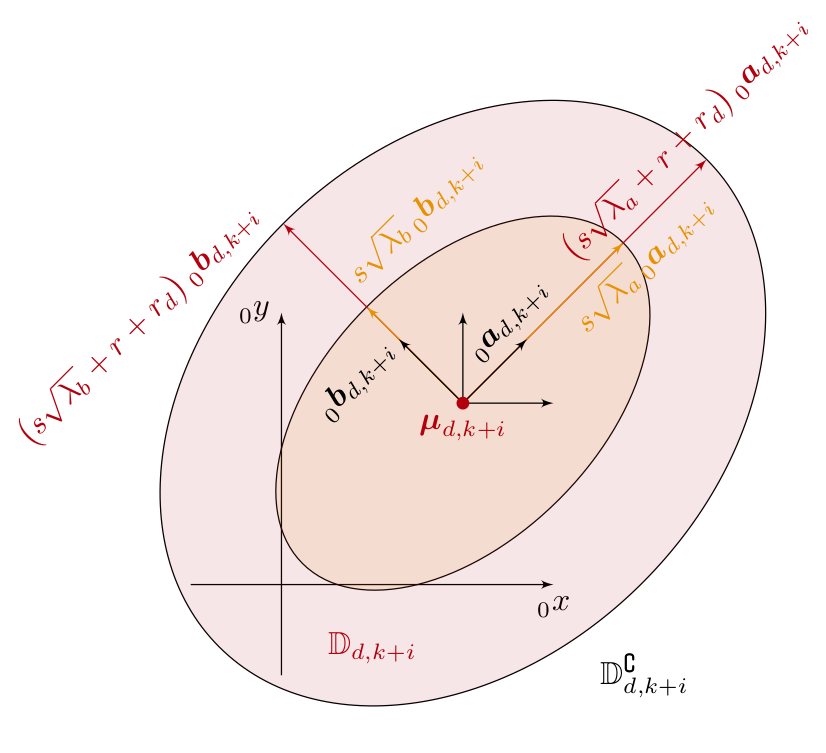
Figure 2: Visual Representation of Ellipse Construction

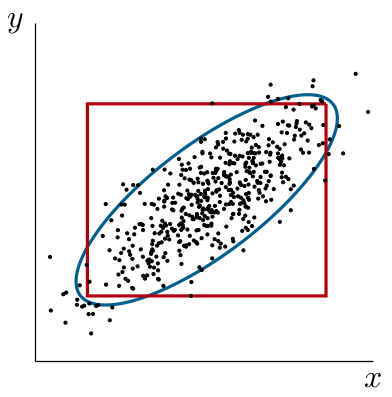
Figure 3: Comparison of different forecast regions for $p=0.90$

Implementation

The trajectory planner is implemented in a Gazebo simulation environment, leveraging ROS2 and Nav2. Two skid-steered robots, equipped with sensors, are simulated with a path planner using Dijkstra's algorithm, and dynamic obstacle positions are communicated between robots. Position predictions employ a VAR(2) process, translating velocity forecasts to positions using statistical models. The system's control structure incorporates an Extended Kalman Filter and velocity smoothing mechanisms, ensuring compatibility with the Nav2 framework and maintaining real-time operation constraints.

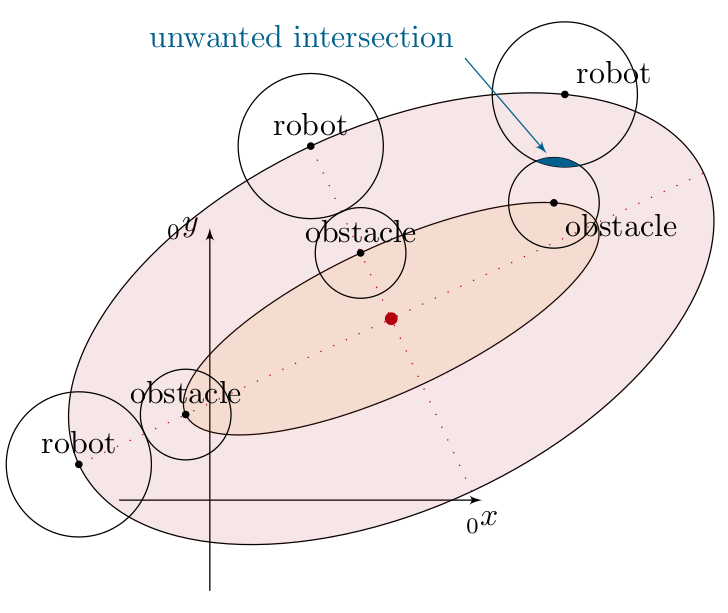
Figure 4: Approximation Error in Ellipse Construction

Results

Simulation scenarios demonstrate the trajectory planner's ability to efficiently navigate and avoid collisions in dynamically changing environments. The visualization captures how robots adapt their paths to account for predicted positions of obstacles, highlighting the planner's predictive capabilities and responsiveness to dynamic challenges. Computational performance metrics indicate acceptable CPU time for solver operations, albeit with occasional spikes due to non-convex problem conditions.

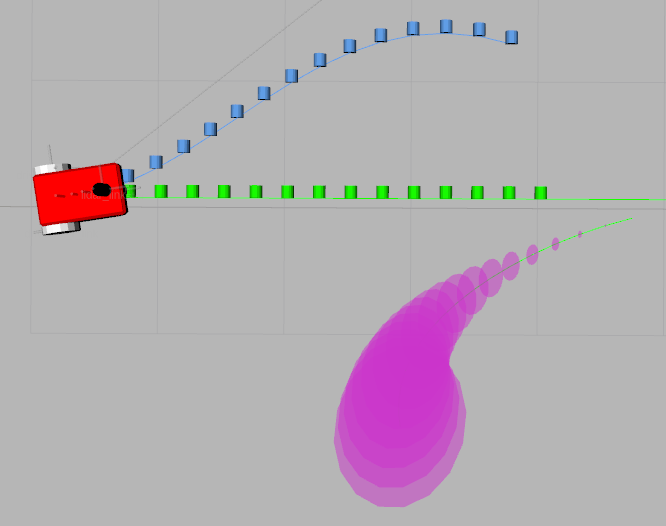
Figure 5: Two robots in a Chicken Game

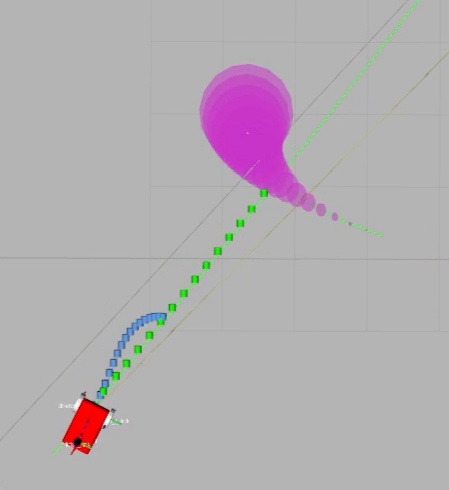
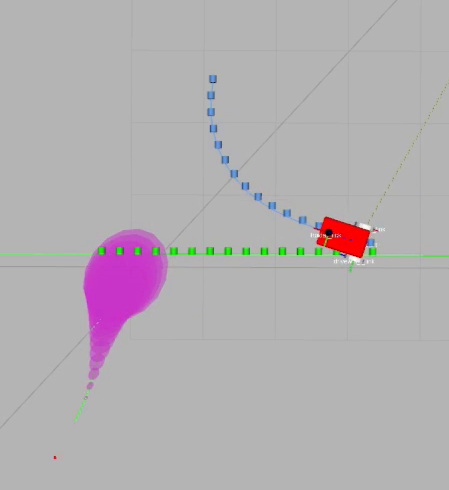
Figure 6: Collision Avoidance

Conclusion and Future Work

The trajectory planner extends Nav2's capabilities by effectively handling dynamic obstacles through prediction-based strategies, improving collision avoidance and adaptability. While current implementations focus on dynamic scenarios, future work will address static obstacle integration and real-world experimentation, further refining the approach. The potential incorporation of dynamic game theory and enhanced obstacle detection and tracking interfaces remain prospective avenues for research, promising robust solutions for autonomous navigation in complex environments.