An MPC framework for efficient navigation of mobile robots in cluttered environments (2509.15917v1)

Abstract: We present a model predictive control (MPC) framework for efficient navigation of mobile robots in cluttered environments. The proposed approach integrates a finite-segment shortest path planner into the finite-horizon trajectory optimization of the MPC. This formulation ensures convergence to dynamically selected targets and guarantees collision avoidance, even under general nonlinear dynamics and cluttered environments. The approach is validated through hardware experiments on a small ground robot, where a human operator dynamically assigns target locations. The robot successfully navigated through complex environments and reached new targets within 2-3 seconds.

• The paper proposes a novel MPC framework which integrates a global planner with local trajectory optimization to enable collision-free navigation.
• It employs Dijkstra's algorithm and an innovative offset cost to overcome challenges posed by non-convex environments.
• Empirical validation with hardware experiments demonstrates the method’s robustness and real-time efficiency on miniature robots.

An MPC Framework for Efficient Navigation of Mobile Robots in Cluttered Environments

In this paper, the authors propose a novel Model Predictive Control (MPC) framework aimed at enhancing the navigation capabilities of mobile robots operating in environments with cluttered obstacles. This framework integrates a shortest path planner within the MPC's trajectory optimization, ensuring a collision-free path towards dynamically selected targets. The paper both theoretically examines and empirically validates its efficacy through hardware experiments on small ground robots.

Figure 1: Visualization of the proposed control approach to navigate through cluttered environments.

Methodology

The proposed MPC framework uniquely integrates a global planner with local trajectory optimization. This integration is achieved by formulating a finite-segment path planning within the MPC's horizon, allowing the system to simultaneously compute a short dynamic path and a discrete long-term path to the target. The framework optimizes the dynamic trajectory considering the robot's geometry, nonlinear dynamics, and real-time environmental constraints, leveraging Dijkstra's algorithm for efficient path initialization.

Collision-Free Path Planning

A critical aspect of the framework is the construction of collision-free path segments. By inflating obstacle boundaries and using a path-connected set of feasible outputs, the system avoids obstacles and safely maneuvers through complex environments.

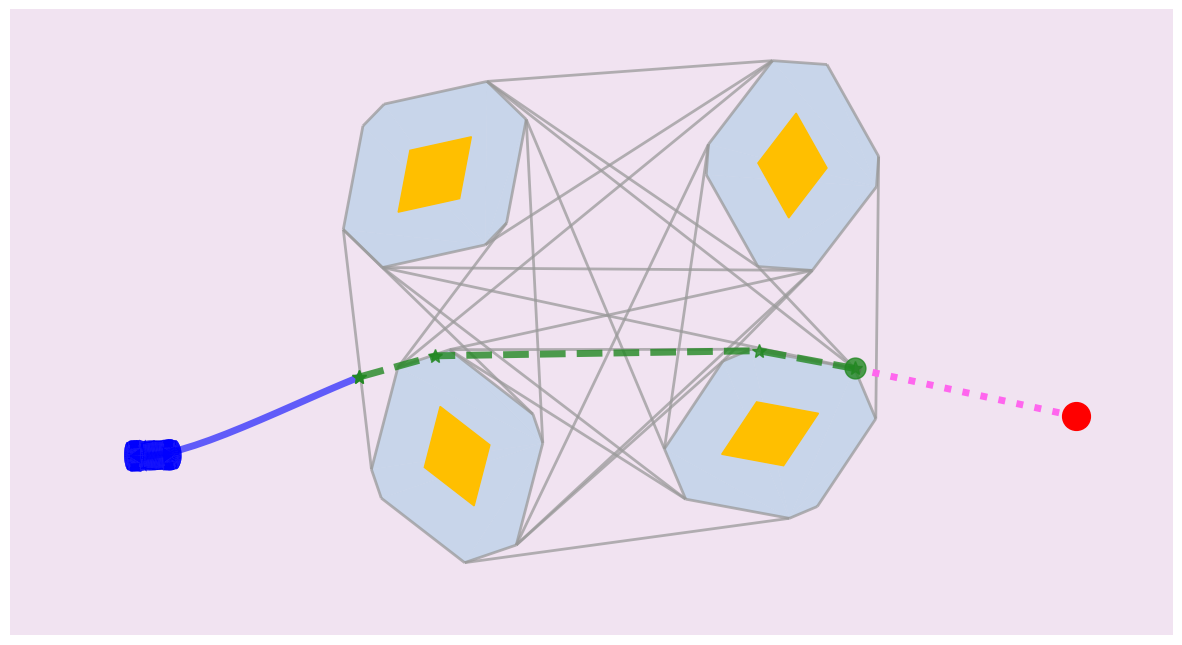
Figure 2: Illustration of the shortest path road map with vehicle, obstacles, and target.

Offset Cost for Non-Convex Environments

The authors introduce an innovative offset cost which evaluates the shortest feasible path length connecting the robot's artificial reference state to the target. This cost function circumvents the limitations of non-convex environments, where traditional distance minimizes can fail.

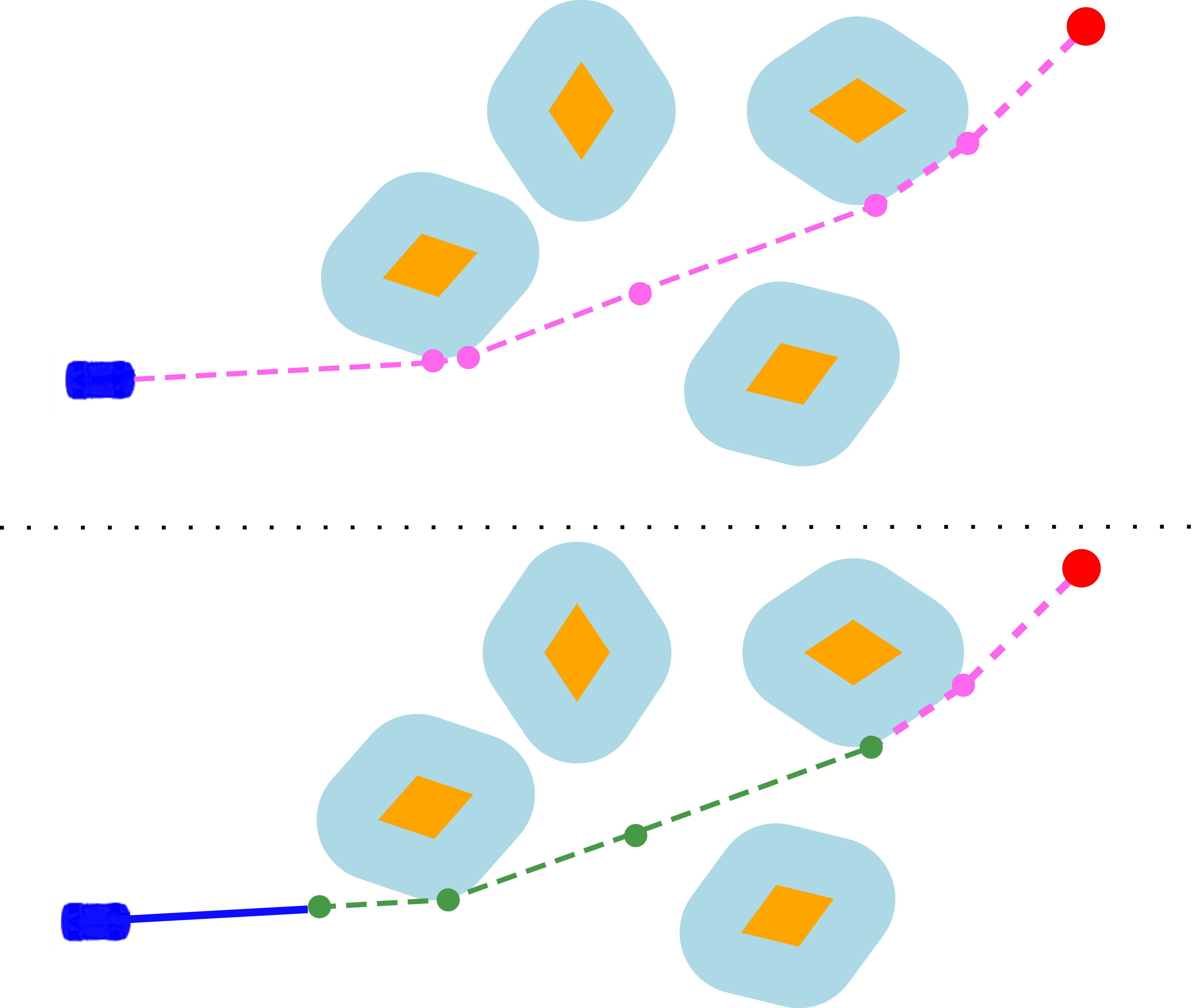
Figure 3: Illustration of the intermediate target with optimized segments differing from the pre-computed shortest path.

Theoretical Guarantees

The paper provides proof of recursive feasibility, collision avoidance, and convergence to the target under general nonlinear dynamics. These guarantees hold by combining the offset cost with a shortest path planner, enabling adaptability to target variations while ensuring safety throughout the motion plan.

Computational Efficiency

Despite the rigorous path planning, the framework maintains computational efficiency, leveraging spatial data structures for collision detection and actively updating intermediate targets to reduce computational loads. The preprocessing and online computation times are minimized, with extensive validation in both sparse and dense environments.

Experimental Validation

Empirical validation is conducted using miniature robotic platforms showcasing the framework's ability to handle real-time dynamic target changes, efficiently reaching new targets within seconds. The experiments further illustrate the controller's robustness in maintaining a collision-free path in complex settings.

Figure 4: Snapshots from hardware experiments using different obstacle setups.

Conclusion

The proposed MPC framework significantly enhances the robotic navigation in cluttered environments by combining adaptive short- and long-term planning. Its theoretical foundations assure safety and target convergence, while computational optimizations ensure real-time applicability. Future research could explore extensions to 3D navigation and dynamic obstacle handling.

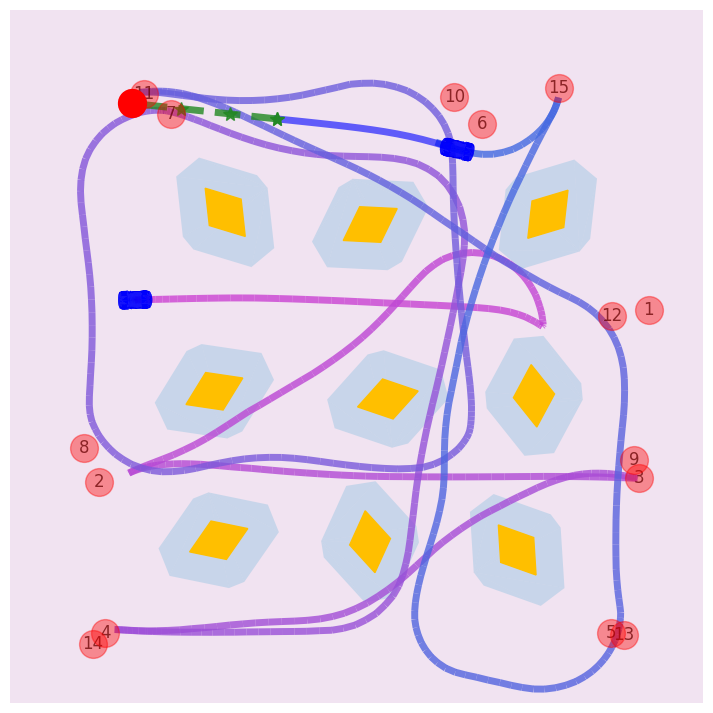
Figure 5: Closed-loop trajectory of hardware experiment, tracking multiple targets.

The research presented herein offers a compelling approach to navigating mobile robots in dynamically obstacles-challenged environments, with implications for applications that demand rapid adaptability and high precision.