In-Sample and Out-of-Sample Sharpe Ratios for Linear Predictive Models (2501.03938v2)

Abstract: We study how much the in-sample performance of trading strategies based on linear predictive models is reduced out-of-sample due to overfitting. More specifically, we compute the in- and out-of-sample means and variances of the corresponding PnLs and use these to derive a closed-form approximation for the corresponding Sharpe ratios. We find that the out-of-sample "replication ratio" diminishes for complex strategies with many assets based on many weak rather than a few strong trading signals, and increases when more training data is used. The substantial quantitative importance of these effects is illustrated with a simulation case study for commodity futures following the methodology of G^arleanu and Pedersen, and an empirical case study using the dataset compiled by Goyal, Welch and Zafirov.

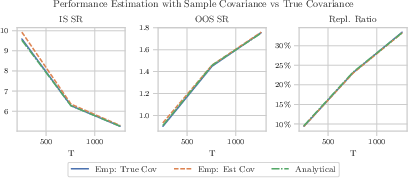
• The paper demonstrates that overfitting in linear predictive models reduces out-of-sample Sharpe ratios, quantified by a declining replication ratio.
• It employs analytical derivations and simulations with Gaussian and AR signals to compare in-sample and out-of-sample performance across trading strategies.
• The study implies that simpler models or larger training samples can mitigate overfitting, thereby improving the reliability of Sharpe ratio estimations.

"In-Sample and Out-of-Sample Sharpe Ratios for Linear Predictive Models" (2501.03938)

This paper investigates the variance reduction in out-of-sample performance of trading strategies based on linear predictive models, attributed to overfitting. It derives an analytical approximation for Sharpe ratios using the in- and out-of-sample means and variances of corresponding PnLs. The model predicts that high complexity, characterized by numerous assets and weak signals or limited training data, leads to diminished out-of-sample performance, quantified as a reduced "replication ratio."

Analytical Framework

The authors adopt a framework wherein predicted asset returns depend linearly on independent and identically distributed (i.i.d.) Gaussian-distributed trading signals. This extends previous models focused on constant investment opportunities by delineating fluctuating signals over time. The theoretical model elucidates that the replication ratio improves with more extended training periods and higher "true" Sharpe ratios, underscoring the vulnerability of complex strategies to overfitting.

Moreover, a simulation using commodity futures showcases the models' practical implications, drawing parallels with the approach by Garleanu and Pedersen (2013). Both Gaussian i.i.d. and autoregressive (AR) signal simulations validate the robustness of analytical approximations, even when assumptions deviate.

Derivation of Key Results

Expected In-Sample and Out-of-Sample PnL

The paper delineates mathematical expressions for the expected values of in-sample and out-of-sample PnLs. For the in-sample scenario, expected inflations emerge from overfitting the model data:

• In-Sample PnL: $\Ex[\widehat{\PnL}_{\text{in-sample}}] = \tr(\Gb\Sigmab_s) + \frac{pm}{T_1}$
• Out-of-Sample PnL: $\Ex[\widehat{\PnL}_{\text{out-sample}}] = \tr(\Gb\Sigmab_s)$

Where $\Gb = \betab^\T\Zb\betab$.

Variability and Covariance Adjustments

Further, the variance and covariance due to estimation errors are detailed. The in-sample variance involves additional terms reflective of covariance discrepancies and measurement errors that vanish in out-of-sample periods when new data is encountered.

Replication Ratio Analysis

The replication ratio, signifying the recoverable percentage of in-sample performance out-of-sample, diminishes with escalating model complexity. This is particularly apparent when $m$ and $p$ are large relative to $T_1$, emphasizing the need for simpler strategies or expanded training samples to maintain high out-of-sample efficacy (Figure 1).

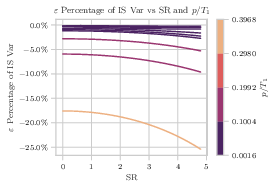
Figure 1: Magnitude of in-sample replication ratio variance components as a function of mean-sample correlation and signal persistence.

Practical Simulations

A detailed simulation with commodity futures and momentum-like signals aligns well with theoretical predictions. The potential performance disparity between simple and complex models is explicated. Notably, panel regression, a technique reducing model parameters by leveraging shared signal responses across assets, curtails overfitting more effectively than fully separate regressions.

Simulation Details

• Gaussian and AR Signal Impact: Replication ratios remain similar with high signal persistence (AR(1)) simulations, suggesting practical robustness of the derived model.
• Covariance Matrix Estimates: Comparisons using both true and estimated covariance matrices in simulations affirm that covariance estimation errors marginally influence performance metrics relative to $\betab$ estimation inaccuracies (Figure 2).

  Figure 2: In- and out-of-sample Sharpe ratio and replication ratio using either the true or estimated covariance matrices.

Conclusion

The paper positions overfitting as a considerable hindrance in out-of-sample performance of linear predictive models applied in trading strategies. For practitioners, recommendations to maintain manageable model complexity and utilize extensive backtesting data are reinforced by analytical findings, with simulation studies corroborating theoretical discussions.

The highlighted investigations invite further empirical validation, especially in real-world market conditions where noise and non-Gaussian distributions are prevalent. Future models might enhance this framework by integrating additional market dynamics and alternative distributions to reflect more diverse market environments.