Generator Matching: Generative modeling with arbitrary Markov processes

Abstract: We introduce Generator Matching, a modality-agnostic framework for generative modeling using arbitrary Markov processes. Generators characterize the infinitesimal evolution of a Markov process, which we leverage for generative modeling in a similar vein to flow matching: we construct conditional generators which generate single data points, then learn to approximate the marginal generator which generates the full data distribution. We show that Generator Matching unifies various generative modeling methods, including diffusion models, flow matching and discrete diffusion models. Furthermore, it expands the design space to new and unexplored Markov processes such as jump processes. Finally, Generator Matching enables the construction of superpositions of Markov generative models and enables the construction of multimodal models in a rigorous manner. We empirically validate our method on image and multimodal generation, e.g. showing that superposition with a jump process improves performance.

• The paper introduces a novel framework that abstracts generative modeling to learning the infinitesimal generators of arbitrary Markov processes.
• It formulates a conditional generator matching loss using Bregman divergences to ensure stable training, effective model superposition, and multimodal extensions.
• Empirical results show that combining jump, flow, and diffusion models improves image and protein generation, yielding state-of-the-art performance on diverse tasks.

Generator Matching: A Unified Framework for Generative Modeling with Arbitrary Markov Processes

Introduction and Motivation

Generator Matching (GM) introduces a modality-agnostic framework for generative modeling that leverages the infinitesimal generators of arbitrary Markov processes. The central abstraction is the generator $\mathcal{L}_t$, which characterizes the infinitesimal evolution of a Markov process and thus the evolution of probability distributions over time. This approach generalizes and unifies existing generative modeling paradigms—including denoising diffusion models, flow matching, and discrete diffusion—by formulating them as special cases of generator learning. GM further expands the design space to include previously unexplored Markov processes, such as jump processes, and enables rigorous construction of multimodal and superposed generative models.

Figure 1: Overview of the Generator Matching (GM) framework, illustrating its applicability to arbitrary state spaces and Markov processes.

Mathematical Foundations

Probability Paths and Conditional Marginals

GM formalizes generative modeling as the construction of a probability path $(p_t)_{t\in[0,1]}$ that interpolates between a tractable prior $p_0$ and the data distribution $p_1$. The conditional probability path $p_t(dx|z)$, parameterized by data point $z$, is designed to be easy to sample from, enabling scalable training via conditional sampling. The marginal path is then $p_t(dx) = \mathbb{E}_{z\sim p_1}[p_t(dx|z)]$.

Markov Processes and Generators

A Markov process $(X_t)_{t\in[0,1]}$ is defined by its transition kernel $k_{t+h|t}$, with the generator $\mathcal{L}_t$ capturing the infinitesimal change in the distribution. The generator is formally defined via test functions $f$ as

$$\mathcal{L}_t f(x) = \lim_{h\to 0} \frac{\mathbb{E}[f(X_{t+h})|X_t=x] - f(x)}{h}$$

and admits universal representations on discrete and Euclidean spaces:

• Discrete: $\mathcal{L}_t f(x) = f^T Q_t^T$ (rate matrix $Q_t$)
• Euclidean: $$\mathcal{L}_t f(x) = \nabla f(x)^T u_t(x) + \frac{1}{2} \nabla^2 f(x) \cdot \sigma_t^2(x) + \int [f(y)-f(x)] Q_t(dy;x)$$

This characterization exhaustively describes the design space for Markovian generative models on $\mathbb{R}^d$ and discrete spaces.

Kolmogorov Forward Equation (KFE)

The evolution of the marginal distribution is governed by the KFE:

$$\partial_t \mathbb{E}_{x\sim p_t}[f(x)] = \mathbb{E}_{x\sim p_t}[\mathcal{L}_t f(x)]$$

Given a conditional generator $\mathcal{L}_t^z$ for $p_t(\cdot|z)$, the marginal generator is

$$\mathcal{L}_t f(x) = \mathbb{E}_{z\sim p_{1|t}(\cdot|x)}[\mathcal{L}_t^z f(x)]$$

This linearity enables scalable training and model combination.

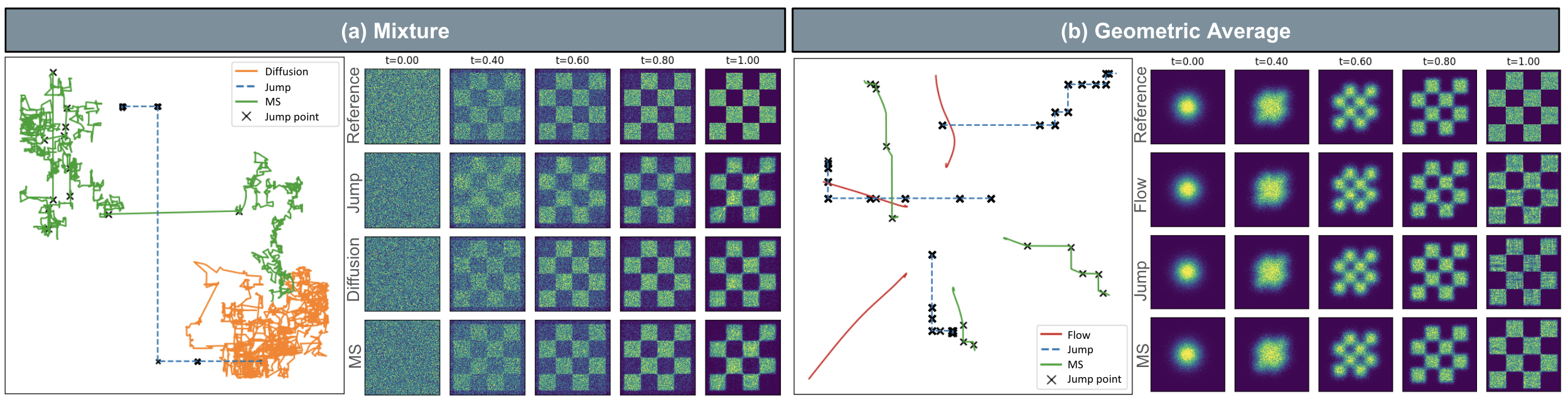
Figure 2: Illustration of sample paths and marginal distributions for different Markov models trained on the same probability path. Marginals are preserved despite distinct sample trajectories.

Training via Generator Matching

Conditional Generator Matching Loss

GM trains a parameterized generator $\mathcal{L}_t^\theta$ (typically via a neural network) to approximate the true marginal generator. The loss is formulated as a conditional generator matching (CGM) objective using Bregman divergences:

$$L_{\text{cgm}}(\theta) = \mathbb{E}_{t, z, x \sim p_t(\cdot|z)} [D(F_t^z(x), F_t^\theta(x))]$$

where $F_t^z$ is the conditional parameterization and $D$ is a Bregman divergence (e.g., MSE, KL). The key result is that minimizing the CGM loss is equivalent (in gradient) to minimizing the intractable marginal generator loss, provided $D$ is a Bregman divergence.

Implementation

• Parameterization: For flows, $F_t = u_t$; for diffusion, $F_t = \sigma_t^2$; for jumps, $F_t = Q_t$.
• Sampling: Euler or higher-order integrators simulate the Markov process using the learned generator.
• Losses: Bregman divergences are used for stable and theoretically justified training.

  Figure 3: Training dynamics of a flow model on CIFAR-10 with different Bregman divergences, demonstrating improved stability and performance over MSE.

Model Combinations and Multimodal Extensions

Markov Superpositions

The linearity of generators and the KFE allows for superposition of models:

$$\mathcal{L}_t^{\text{super}} = \alpha_t^1 \mathcal{L}_t + \alpha_t^2 \mathcal{L}_t'$$

where $\alpha_t^1 + \alpha_t^2 = 1$. This enables combining flows, diffusions, and jumps, yielding improved performance and flexibility.

Multimodal Modeling

GM rigorously constructs multimodal generative models by combining unimodal generators on product spaces $S_1 \times S_2$. The marginal generator is the sum of the unimodal generators, and training decomposes into independent losses per modality, greatly simplifying high-dimensional and multimodal generative modeling.

Empirical Results

Image Generation

Jump models, a novel class for $\mathbb{R}^d$, are shown to generate realistic images, albeit with lower FID scores than state-of-the-art flow models. However, Markov superpositions of jump and flow models outperform pure flows, especially when combining different samplers.

Figure 4: Examples of generated images on CIFAR10 (top) and ImageNet32 (bottom) using jump and flow models.

Protein Structure Generation

GM enables multimodal generative modeling for protein sequence and structure. Incorporating $SO(3)$ jump models into MultiFlow yields state-of-the-art diversity and novelty metrics, outperforming previous baselines.

Figure 5: Examples of generated proteins with $SO(3)$ jumps and MultiFlow, each passing designability and being structurally unique.

Systematic Study of Probability Paths and Markov Models

A systematic ablation over probability paths (mixture, CondOT) and Markov model classes (flow, diffusion, jump, superposition) reveals that performance and discretization error are highly dependent on the choice of path and model. Flows excel on CondOT paths, jumps on mixture paths, and superpositions often yield the best results.

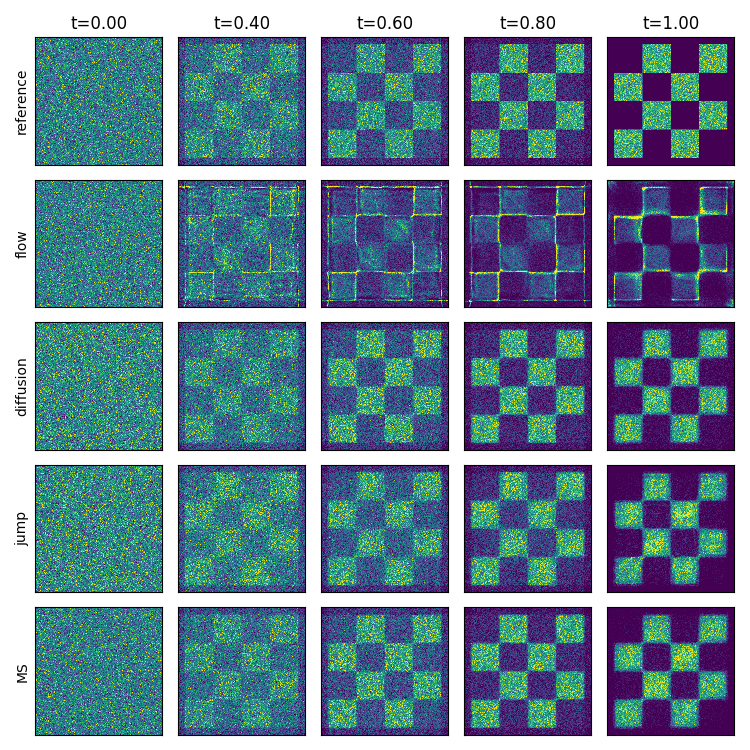
Figure 6: 2D histograms of generated samples for mixture path models, showing jump models outperform flows on discontinuous paths.

Figure 7: 2D histograms for CondOT path models, with flows outperforming jumps on continuous transport paths.

Figure 8: NFE ablation for mixture path, showing jump models are less sensitive to discretization error.

Figure 9: NFE ablation for CondOT path, showing flows are less sensitive to discretization error.

Theoretical and Practical Implications

GM provides a rigorous foundation for generative modeling with arbitrary Markov processes, unifying disparate approaches and enabling principled exploration of new model classes. The framework's linearity facilitates model combination, multimodal extensions, and systematic loss design via Bregman divergences. Practically, GM enables scalable training, flexible architecture choices, and improved sample quality through superposition and multimodal integration.

Future Directions

Potential avenues include:

• Learning state-dependent diffusion coefficients and jump kernels for richer dynamics.
• Developing efficient samplers and distillation techniques to reduce computational cost.
• Extending GM to more complex manifolds and trans-dimensional state spaces.
• Systematic exploration of Bregman divergences for improved training stability and generalization.

Conclusion

Generator Matching establishes a unified, scalable, and theoretically grounded framework for generative modeling with arbitrary Markov processes. By abstracting generative modeling to the learning of infinitesimal generators, GM subsumes existing paradigms and opens new directions for model design, combination, and multimodal integration. The empirical and theoretical results demonstrate the framework's versatility and potential for advancing generative modeling across diverse domains.