Entropy Computing, A Paradigm for Optimization in Open Photonic Systems

Abstract: Finding better solutions to combinatorial optimization problems could have a large positive impact on many real-world application areas, such as logistics. For this reason, significant efforts have been made to design novel optimisation paradigms. Here we show an early instance of such paradigm in an optical setting, the entropy computing paradigm. Specifically, we experimentally demonstrate the feasibility of entropy computing by building a hybrid photonic-electronic computer that uses optical measurement and feedback to solve non-convex optimization problems. The system functions by using temporal photonic modes to create qudits in order to encode probability amplitudes in the time-frequency degree of freedom of a photon. This scheme, when coupled with with electronic interconnects, allows us to encode an arbitrary Hamiltonian into the system and solve non-convex continuous variables and combinatorial optimization problems. We show that the proposed entropy computing paradigm can act as a scalable and versatile platform for tackling a large range of NP-hard optimization problems.

• The paper introduces entropy computing as a novel method to tackle NP-hard optimization via hybrid photonic-electronic techniques.
• It details the implementation of the Dirac-3 optimization machine, using time-bin encoded photonic qudits and nonlinear feedback to solve complex polynomial functions.
• Benchmark results show the system's superior performance in graph partitioning compared to semi-definite programming, indicating potential energy efficiency and scalability.

"Entropy Computing, A Paradigm for Optimization in Open Photonic Systems" (2407.04512)

Introduction

In this paper, the authors introduce the paradigm of "entropy computing" as a novel method for addressing NP-hard optimization problems. This involves an experimental setup using a hybrid photonic-electronic framework that effectively manipulates quantum states encoded as photonic qudits. The proposed entropy computing paradigm leverages the temporal modes of photons, advanced hybrid feedback mechanisms, and nonlinear interactions within optical circuits to embed and solve complex Hamiltonians, presenting an alternative computational strategy that aims to outperform traditional approaches.

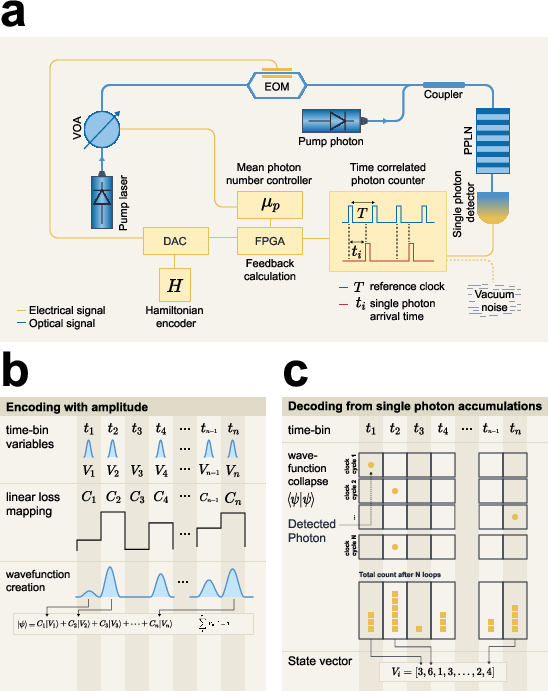
Figure 1: An emulation system for entropy computing using time-energy modes and a measurement-feedback scheme.

Hybrid Entropy Computing System

The experimental setup outlined in the paper utilizes time correlated single photon counting (TCSPC) combined with electro-optical feedback mechanisms. The system functions by encoding real-number variables into time-bin photonic qudit states. The architecture involves several components — a laser source, electro-optic modulation, nonlinear optical processing, and a single-photon detection system, all orchestrated through a Field Programmable Gate Array (FPGA) enabling dynamic computation in real-time. This setup is instrumental in solving polynomial optimization problems characterized by complex and non-convex characteristics due to the inherent quantum fluctuations, facilitating rapid exploration of solution landscapes.

Implementation of Dirac-3 Optimization Machine

The entropy computing paradigm provides the foundation for the Dirac-3 optimization machine, which capitalizes on hybrid optoelectronic interactions for executing complex mathematical formulations up to the fifth order polynomial functions efficiently. The Dirac-3 system demonstrates significant capabilities in solving a host of optimization problems, including binary, integer, and mixed-integer formulations. Unique to this approach is its ability to maintain a discrete representation of variables over continuous states, ensuring comprehensive interaction encoding without necessitating auxiliary variables for expanded problem representation.

Benchmarked Results

The authors experimentally evaluated the hybrid system using well-defined non-convex optimization instances, including two-variable polynomial functions and combinatorial graph partitioning problems. The results unequivocally demonstrate the advantages of entropy computing over traditional methods. In particular, for graph-based partitioning (max-k-cut problems), the machine exhibits superior performance, frequently outperforming semi-definite programming (SDP) approaches, highlighting its broad applicability and efficacy in handling complex interactions that characterize NP-hard problems.

Figure 2: The results for solving the max-k-cut problem.

Discussion

The entropy computing model leverages quantum effects embodying coherent state dynamics and fundamental randomness induced through photon interaction. This inherently stochastic approach enables efficient navigation of search space while avoiding local minima traps common in classical algorithms. The tantalizing prospect of transitioning toward an all-optical entropy computing framework inherently suggests potential scaling benefits and a significant reduction in energy consumption relative to conventional computing paradigms. Further research is anticipated to explore and optimize this paradigm's integration within quantum annealing domains.

Conclusion

The study delineates an innovative approach to optimization leveraging photonic processing capabilities, setting a precedent for future quantum-adjacent computing developments. Notably, Dirac-3's successful implementation reaffirms the versatility and potential superiority of entropy computing in tackling vast computational problems with practical implications across various domains, from logistics to abstract machine learning tasks.