Programmable 200 GOPS Hopfield-inspired photonic Ising machine (2509.09581v1)

Abstract: Ising machines offer a compelling approach to addressing NP-hard problems, but physical realizations that are simultaneously scalable, reconfigurable, fast, and stable remain elusive. Quantum annealers, like D-Wave's cryogenic hardware, target combinatorial optimization tasks, but quadratic scaling of qubit requirements with problem size limits their scalability on dense graphs. Here, we introduce a programmable, stable, room-temperature optoelectronic oscillator (OEO)-based Ising machine with linear scaling in spin representation. Inspired by Hopfield networks, our architecture solves fully-connected problems with up to 256 spins (65,536 couplings), and $>$41,000 spins (205,000+ couplings) if sparse. Our system leverages cascaded thin-film lithium niobate modulators, a semiconductor optical amplifier, and a digital signal processing (DSP) engine in a recurrent time-encoded loop, demonstrating potential $>$200 giga-operations per second for spin coupling and nonlinearity. This platform achieves the largest spin configuration in an OEO-based photonic Ising machine, enabled by high intrinsic speed. We experimentally demonstrate best-in-class solution quality for Max-Cut problems of arbitrary graph topologies (2,000 and 20,000 spins) among photonic Ising machines and obtain ground-state solutions for number partitioning and lattice protein folding - benchmarks previously unaddressed by photonic systems. Our system leverages inherent noise from high baud rates to escape local minima and accelerate convergence. Finally, we show that embedding DSP - traditionally used in optical communications - within optical computation enhances convergence and solution quality, opening new frontiers in scalable, ultrafast computing for optimization, neuromorphic processing, and analog AI.

• The paper demonstrates a programmable, room-temperature OEO-based Ising machine, achieving over 200 GOPS via cascaded TFLN modulators, DSP, and controlled noise injection.
• The paper validates its architecture through detailed experimental characterizations including bifurcation dynamics, 96.2% MVM accuracy, and benchmarks on square lattice, Max-Cut, and protein folding problems.
• The paper achieves linear spin scaling and sub-4.1 μs feedforward latency, paving new directions for analog AI, neuromorphic computing, and scalable photonic optimization.

Programmable 200 GOPS Hopfield-Inspired Photonic Ising Machine: Architecture, Performance, and Implications

Introduction and Motivation

This work presents a programmable, room-temperature optoelectronic oscillator (OEO)-based Ising machine, leveraging cascaded thin-film lithium niobate (TFLN) modulators, a quantum-dot semiconductor optical amplifier (QD SOA), and a digital signal processing (DSP) engine in a recurrent time-encoded loop. The architecture is inspired by Hopfield networks and is designed to solve combinatorial optimization problems mapped to the Ising Hamiltonian, including Max-Cut, number partitioning, and protein folding. The system demonstrates linear scaling in spin representation, supporting up to 256 fully connected spins (65,536 couplings) and over 41,000 sparsely connected spins (205,000+ couplings), with a feedforward latency of $\sim$4.1 $\mu$s and computational throughput exceeding 200 GOPS.

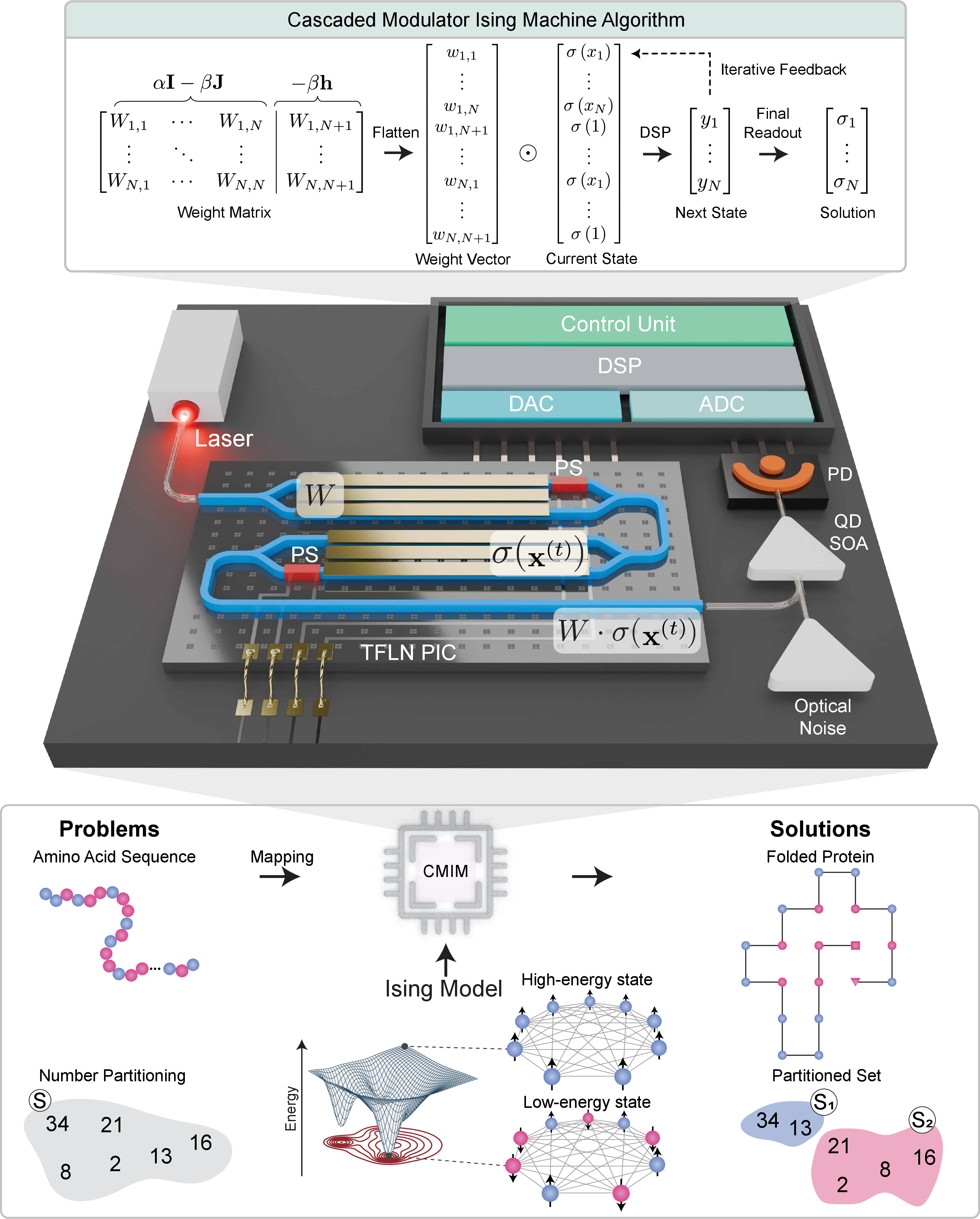
Figure 1: Conceptual illustration of the CMIM, mapping combinatorial optimization problems to the Ising model and showing the hardware feedback loop with cascaded TFLN modulators, SOA, DSP, and photodetection.

System Architecture and Operational Principle

The CMIM architecture reformulates the Ising energy minimization as a matrix-vector multiplication (MVM) problem, with the weight matrix $\mathbf{W}$ and spin vector $\mathbf{X}$ encoded optically. Two cascaded TFLN Mach-Zehnder modulators (MZMs) perform nonlinear and linear modulation, respectively, followed by element-wise multiplication and summation via QD SOA and photodetection. High-speed feedback is achieved using ADC/DAC modules at 256 GSa/s, enabling iterative convergence to the ground state. The system emulates continuous-domain Hopfield dynamics with controllable stochastic perturbations, and hyperparameters ($\alpha$, $\beta$) are tuned for rapid convergence and stability. DSP is embedded to compensate for signal impairments at high baud rates, and inherent noise from high-speed operation is exploited for annealing.

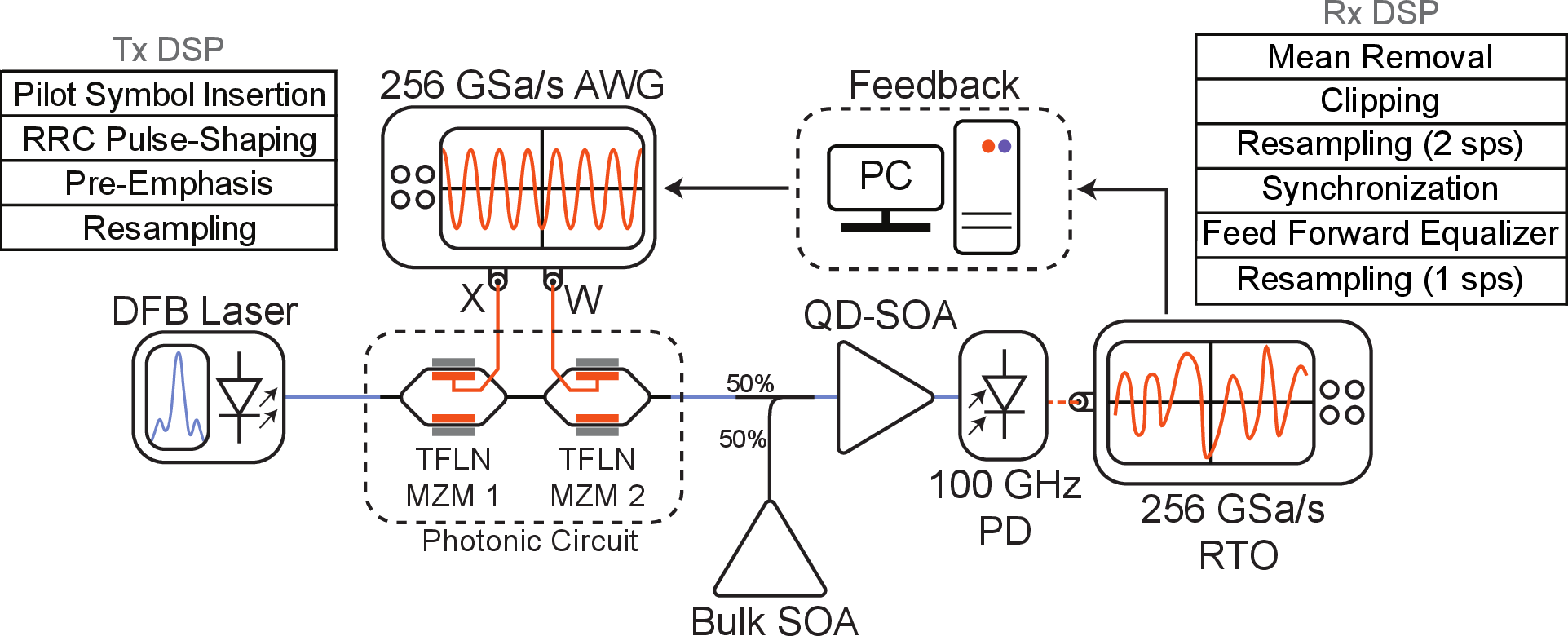
Figure 2: Detailed experimental schematic of the CMIM, showing the signal generation, modulation, detection, and DSP feedback pipeline.

Experimental Characterization: Bifurcation and MVM

Bifurcation dynamics, a haLLMark of Ising systems, were experimentally characterized as a function of feedback strength $\alpha$. The system transitions from monostability to bistability above a critical $\alpha_0$, with spins converging to two stable fixed points. MVM accuracy was validated at 106 GBaud, achieving 212 GOPS and 96.2% accuracy for 128$\times$128 matrices. Bit precision decreases linearly with increasing baud rate, from 5.03 bits at 4 GBaud to 2.79 bits at 148 GBaud, primarily due to noise and distortion. Notably, this analog degradation acts as an annealing mechanism, aiding escape from local minima.

Figure 3: Experimental bifurcation dynamics, MVM accuracy, and bit precision scaling with baud rate.

Benchmarking: Square Lattice and Max-Cut

The CMIM was benchmarked on 2D square lattice and Max-Cut problems (G22 and G81 graphs). For the square lattice, ground state solutions were achieved for up to 10,201 spins, with solution quality exceeding 97.2% for 41,209 spins. Max-Cut experiments on G22 (2,000 nodes) and G81 (20,000 nodes) graphs yielded 99.48% and 96.34% of best-known cut values, respectively, outperforming prior photonic Ising machines. The system's performance is attributed to controllable optical noise injection (bulk SOA) and DSP-based amplitude clipping, with further improvements anticipated via advanced algorithms (chaotic amplitude control, momentum-based methods).

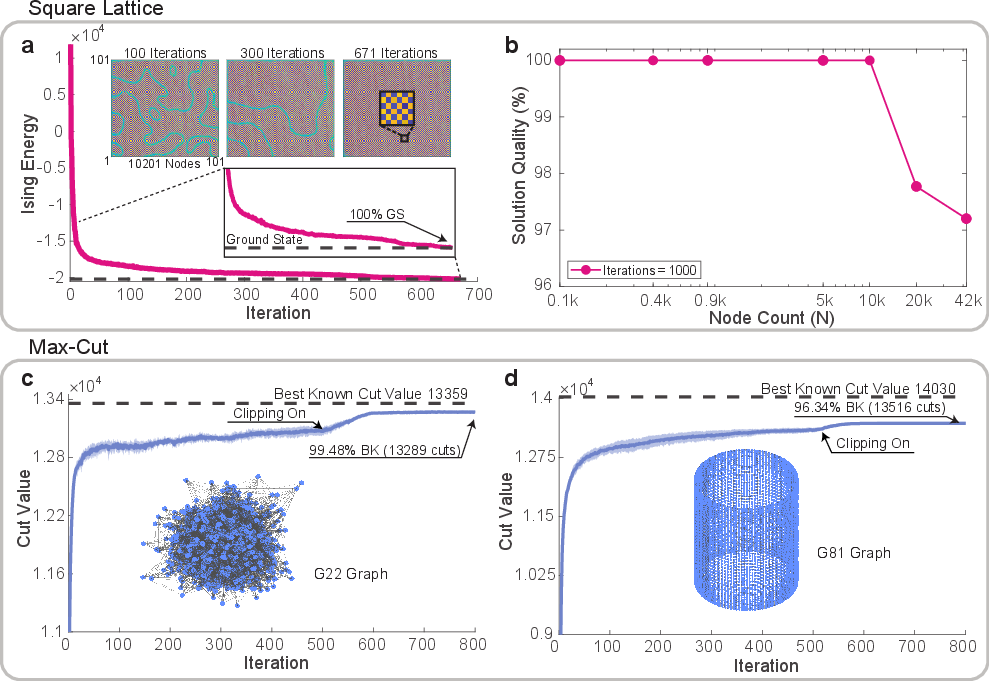
Figure 4: Benchmarking results for square lattice and Max-Cut problems, showing energy/cut value evolution and scaling analysis.

Protein Folding: HP Model

Protein folding was addressed using the HP lattice model, mapping amino acid sequences to Ising spin configurations. The CMIM achieved ground-state solutions for sequences up to $S_{10}$ (100% hit rate) and maintained solution quality above 99% for $S_{30}$. The approach is competitive with quantum annealing (D-Wave), but with architectural advantages: linear scaling, room-temperature operation, and native support for arbitrary connectivity without auxiliary spins.

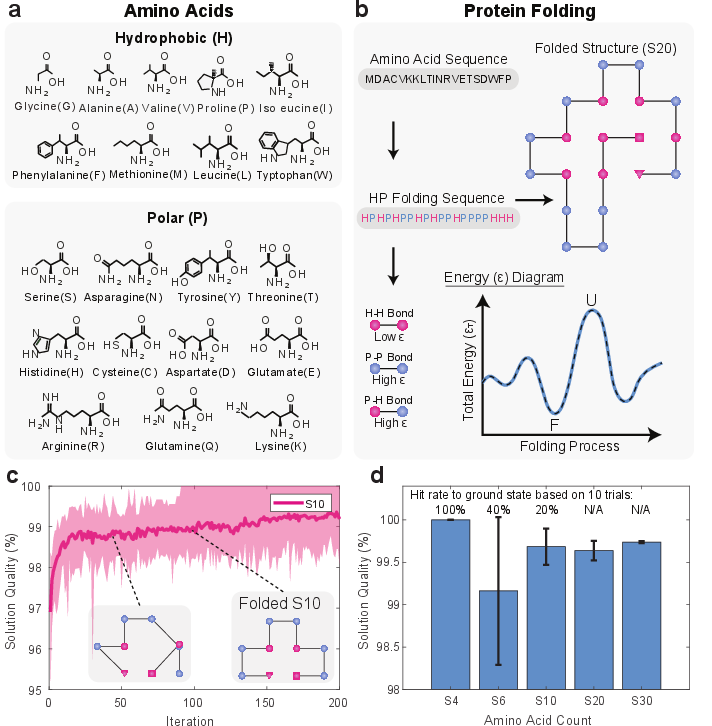
Figure 5: HP model protein folding, mapping, energy landscape evolution, and solution quality for increasing sequence lengths.

Number Partitioning

The number partitioning problem, an NP-hard task with exponential solution space, was solved for problem sizes up to $N=256$ with 100% success rate. Computation time to solution scales exponentially with problem size, consistent with theoretical complexity. In contrast to D-Wave's quantum annealer, which exhibits quadratic scaling and rapidly decreasing success probability for $N>32$, the CMIM maintains high fidelity and scalability, limited only by current hardware memory.

(Figure 6)

Figure 6: Number partitioning problem illustration and scaling of computation time and success probability for CMIM and D-Wave.

Noise Injection and Annealing

Controlled optical noise injection via bulk SOA was systematically characterized. Gaussian-distributed ASE noise was tuned via SOA bias current, with optimal noise levels accelerating convergence. Exponential annealing schedules further reduced iteration counts to ground state, demonstrating the utility of hardware-level noise control for optimization.

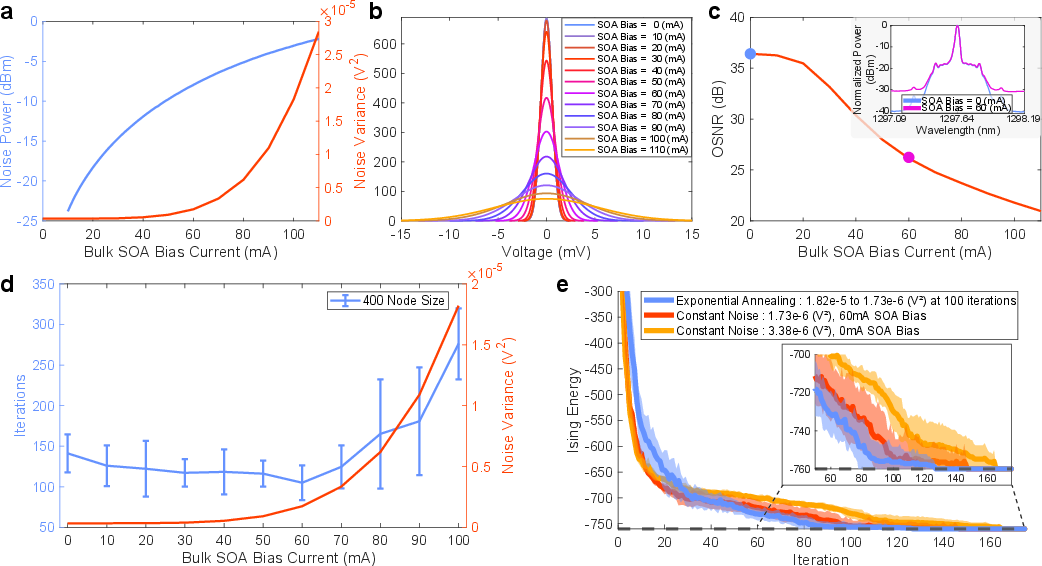
Figure 7: Optical noise injection characterization, OSNR scaling, and impact on convergence for square lattice problems.

Implementation Considerations and Scaling

The CMIM is robust to ambient variations (voltage, optical power, temperature), with DSP compensating for hardware imperfections. Feedback latency is currently limited by discrete DAC/ADC components, but pipelined DSP implementations (e.g., Ciena Wavelogic ASICs) can reduce latency to sub-microsecond levels. Multidimensional multiplexing (TDM, SDM, WDM) can further scale throughput, with projected architectures supporting over 30 million spins and compute efficiency surpassing state-of-the-art GPUs (NVIDIA H100).

Implications and Future Directions

The demonstrated CMIM advances photonic Ising machines in scalability, speed, programmability, and stability. It achieves best-in-class performance on combinatorial optimization benchmarks, with architectural advantages over quantum annealers and electronic platforms. The integration of DSP and photonic hardware principles opens new directions for analog AI, neuromorphic computing, and ultrafast heuristic solvers. Future work should focus on full integration, advanced algorithmic control, and multidimensional multiplexing to further enhance throughput and problem size.

Conclusion

This work establishes a Hopfield-inspired, programmable photonic Ising machine capable of solving large-scale, NP-hard optimization problems with high fidelity and speed. The architecture leverages cascaded TFLN modulators, DSP, and controlled noise injection to achieve robust, scalable operation. The system outperforms prior photonic and quantum hardware on key benchmarks, and its design principles provide a foundation for next-generation analog AI accelerators and photonic computing platforms.