Sampling-Based Optimization for Multi-Agent Model Predictive Control (2211.11878v1)

Abstract: We systematically review the Variational Optimization, Variational Inference and Stochastic Search perspectives on sampling-based dynamic optimization and discuss their connections to state-of-the-art optimizers and Stochastic Optimal Control (SOC) theory. A general convergence and sample complexity analysis on the three perspectives is provided through the unifying Stochastic Search perspective. We then extend these frameworks to their distributed versions for multi-agent control by combining them with consensus Alternating Direction Method of Multipliers (ADMM) to decouple the full problem into local neighborhood-level ones that can be solved in parallel. Model Predictive Control (MPC) algorithms are then developed based on these frameworks, leading to fully decentralized sampling-based dynamic optimizers. The capabilities of the proposed algorithms framework are demonstrated on multiple complex multi-agent tasks for vehicle and quadcopter systems in simulation. The results compare different distributed sampling-based optimizers and their centralized counterparts using unimodal Gaussian, mixture of Gaussians, and stein variational policies. The scalability of the proposed distributed algorithms is demonstrated on a 196-vehicle scenario where a direct application of centralized sampling-based methods is shown to be prohibitive.

• The paper presents a novel distributed sampling-based optimization framework that significantly boosts scalability in MPC systems.
• It integrates stochastic search, variational optimization, and variational inference with ADMM to decentralize and streamline multi-agent control.
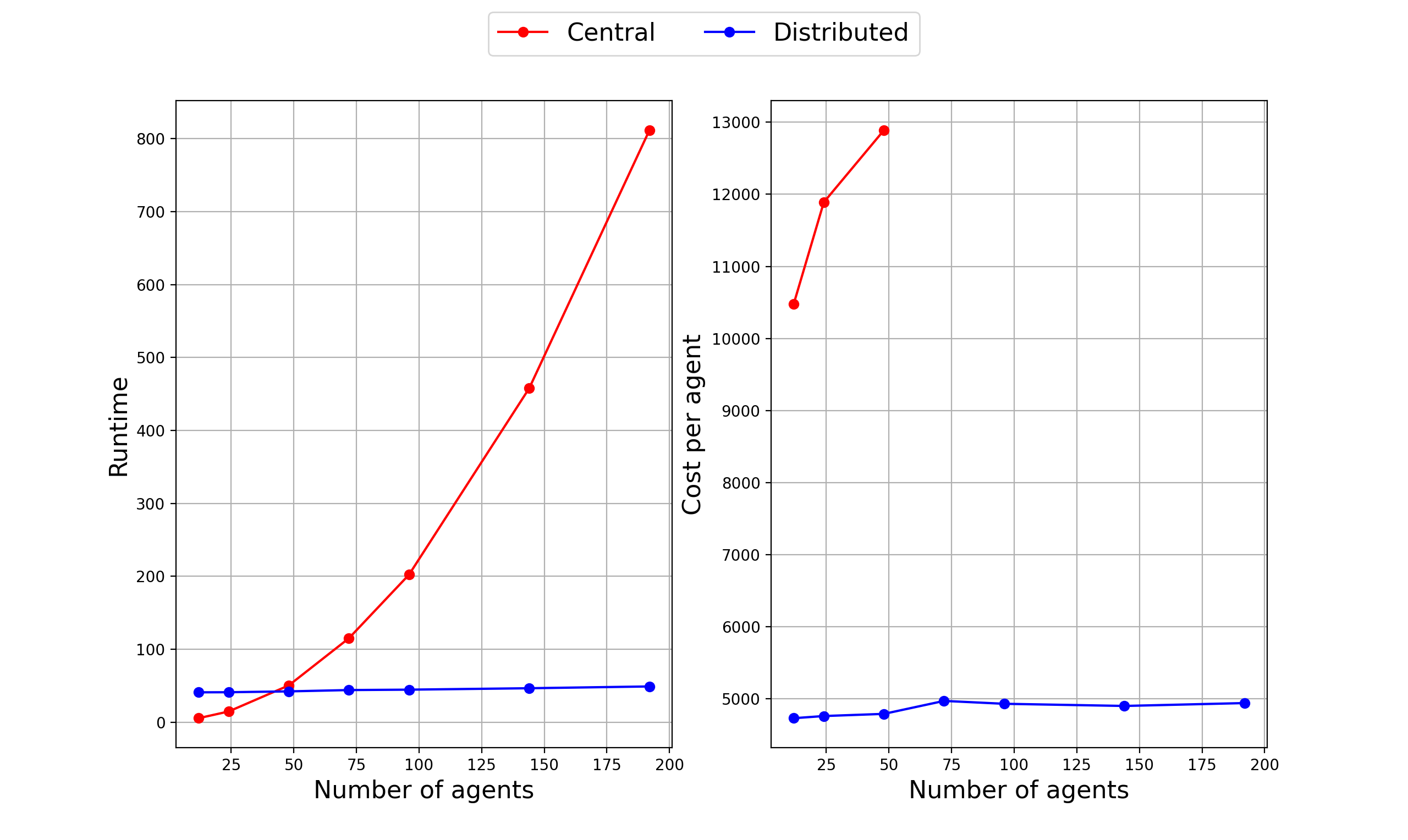
• Simulations using vehicular and quadcopter systems show improved runtime and cost metrics over traditional centralized approaches.

Sampling-Based Optimization for Multi-Agent Model Predictive Control

This paper presents a novel approach for sampling-based optimization in multi-agent model predictive control (MPC) systems, focusing on enhancing scalability and efficiency through distributed frameworks.

Introduction

The research systematically reviews three primary approaches to sampling-based dynamic optimization: Variational Optimization (VO), Variational Inference (VI), and Stochastic Search (SS). These methodologies are examined in the context of Multi-Agent MPC, where the computational complexity poses significant challenges as the number of agents increases. Traditional centralized control techniques are inefficient at scale due to their computational demands, making the paper of distributed optimization both relevant and necessary.

Methodology

Sampling-Based Optimization Techniques

The paper reviews and unifies different sampling-based dynamic optimization methods from the perspectives of SS, VO, and VI. Each technique involves generating decision variables from a sampling distribution, which is iteratively updated.

1. Stochastic Search (SS): This approach involves computing gradients of the expected cost transform via sampling and guiding the optimization through steepest ascent on the transformed objective function.
2. Variational Optimization (VO): Derives optimizers based on Kullback-Leibler divergence minimization with Gibbs distribution as the target distribution, offering connections to Hamilton-Jacobi-Bellman theory in SOC.
3. Variational Inference (VI): Converts the control problem into a Bayesian inference problem, thus allowing for optimality likelihood parameterization, often employing Tsallis divergence for more flexibility.

Distributed MPC Framework

To address scalability issues, the paper proposes a distributed MPC framework utilizing the consensus-based Alternating Direction Method of Multipliers (ADMM). This framework allows the decoupling of a large-scale optimization problem into more manageable sub-problems at the neighborhood level, facilitating parallelization. In this model, each agent performs local optimization while enforcing consistency constraints with its neighbors, thus achieving full decentralization.

Simulation and Results

The proposed methodologies are validated through simulation on complex multi-agent tasks involving vehicular and quadcopter systems. The simulation comparisons demonstrate the scalability of the distributed approach with up to 196 agents by showing reduced computational times and enhanced task performance compared to centralized methods.

Key Findings:

• The distributed framework showed significant improvements over centralized methods in terms of mean cost and variance.
• Computational efficiency was observed with increasing numbers of agents, confirming the hypothesis of improved scalability.
• Preference for Tsallis VI and SS approaches was noticed due to their flexibility and robustness in complex settings.

  Figure 1: Scaling comparison between the Central and Distributed scheme on the Dubins formation experiment. Left: Runtime comparison; Right: Cost per agent comparison. The missing data points for the central scheme indicate crashing result.

Conclusion

The paper contributes a robust, distributed approach to MPC that significantly boosts scalability and efficiency for multi-agent systems. By incorporating ADMM into sampling-based optimization, the researchers successfully expand the practical applicability of MPC to complex, large-scale, multi-agent problems. Future work may explore the integration with real-world systems and further refine policy distribution techniques to enhance decision quality across diverse scenarios.