Sliced ReLU attention: Quasi-linear contextual expressivity via sorting

Abstract: We introduce sliced ReLU attention, a new attention mechanism that departs structurally from both softmax and ReLU-based alternatives. Instead of applying a nonlinearity to pairwise dot products, we operate on one-dimensional projections of key--query differences and leverage sorting to obtain quasi-linear complexity. This construction yields a differentiable, non-symmetric kernel that can be computed in O(n log(n)) through a sorting procedure, making it suitable for very long contexts. Beyond computational benefits, the model retains strong theoretical expressive power: we establish two in-context expressivity results, previously known for softmax attention, showing that sliced ReLU attention preserves the ability to perform nontrivial sequence-to-sequence disentangling tasks and satisfies a contextual universal approximation property. Finally, we illustrate the potential practical interest of this kernel in small-scale experiments.

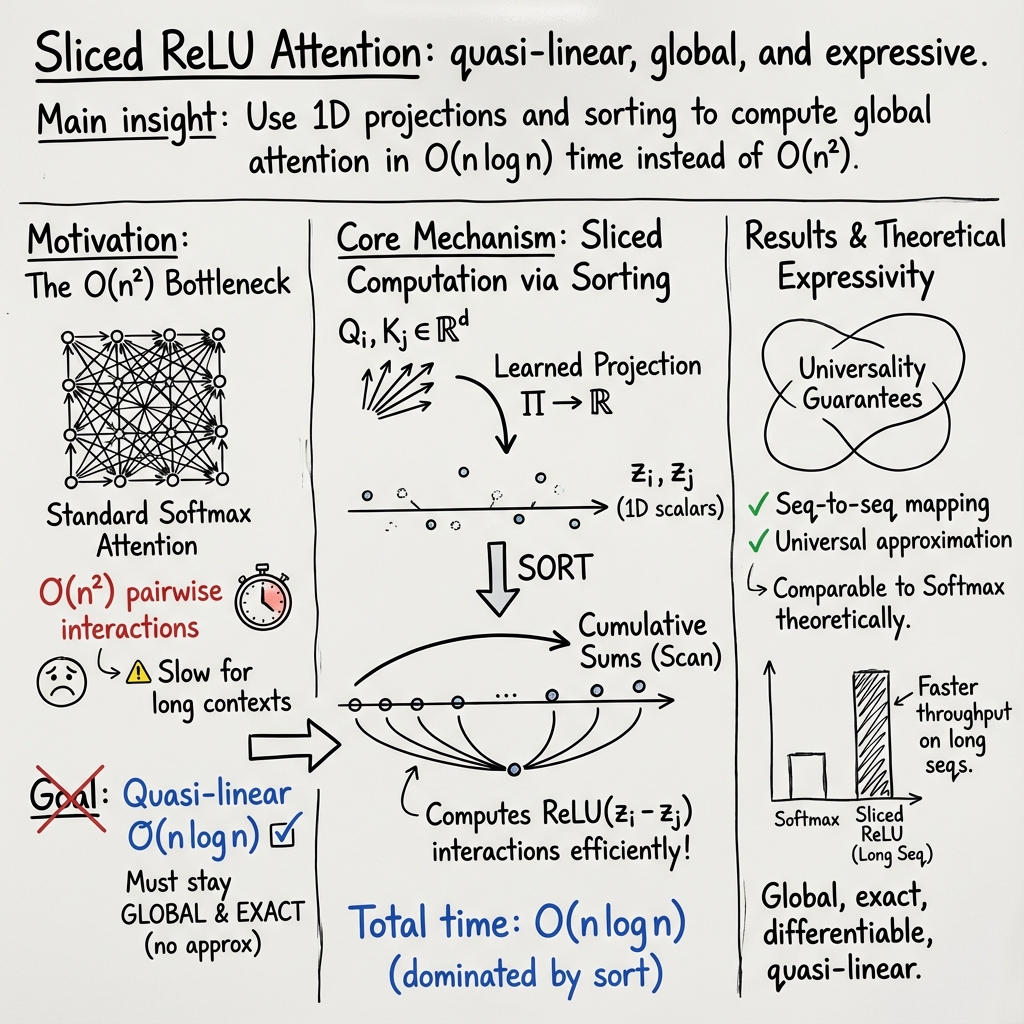
• The paper presents a novel attention mechanism that employs one-dimensional projections and sorting to reduce quadratic complexity to quasi-linear O(n log n).
• The methodology leverages a differentiable, non-symmetric ReLU kernel to retain softmax-level contextual expressivity while enabling efficient long-sequence processing.
• Empirical benchmarks show competitive performance on long-range reasoning tasks, highlighting its promise for scalable deep learning applications.

Sliced ReLU Attention: Quasi-Linear Complexity via Sorting

Introduction

The paper "Sliced ReLU attention: Quasi-linear contextual expressivity via sorting" (2512.11411) introduces a novel attention mechanism designed to improve computational efficiency while retaining theoretical expressivity. Traditional attention mechanisms in Transformers face challenges due to their quadratic computational complexity concerning input sequence length, limiting their application in tasks involving long sequences like document summarization or high-resolution image analysis. The sliced ReLU attention mechanism circumvents this bottleneck by operating on one-dimensional projections of key-query differences, leveraging sorting to achieve quasi-linear complexity in $O(n\log(n))$ time.

Sliced ReLU Attention Mechanism

This approach departs structurally from both softmax and ReLU-based alternatives by focusing on nonlinearity applied to the differences between projected keys and queries rather than pairwise dot products. The sliced ReLU attention mechanism leverages sorting to optimize computational complexity. It adopts a differentiable non-symmetric kernel computed efficiently through sorting, making it well-suited for very long contexts.

Figure 1: Illustration of geometric interaction patterns induced by sliced ReLU attention for two different projection operators $\Pi$. The geometry of the projection directly shapes the interaction pattern.

Expressivity and Practical Applications

Theoretically, the sliced ReLU kernel retains strong expressivity similar to that of softmax-based attention. The paper demonstrates two expressivity results: it shows that sliced ReLU attention can perform nontrivial sequence-to-sequence disentangling tasks and satisfies a contextual universal approximation property. These properties suggest that sliced ReLU attention can serve as a universal approximator, key in the successful application across various tasks.

Empirically, the potential of this attention mechanism is illustrated through experiments on standard Transformer benchmarks. The task performance reveals that sliced ReLU attention is competitive with softmax attention, often matching or exceeding its efficacy on long-range reasoning tasks.

Computational Complexity and Efficiency

A major advantage of the sliced ReLU attention mechanism is its computational complexity. By sorting one-dimensional projections, it provides a scalable solution to the quadratic time complexity inherent in traditional attention models. This efficiency allows for precise global interactions without the need for approximations, making it a promising choice for applications requiring long-range or extensive token interactions.

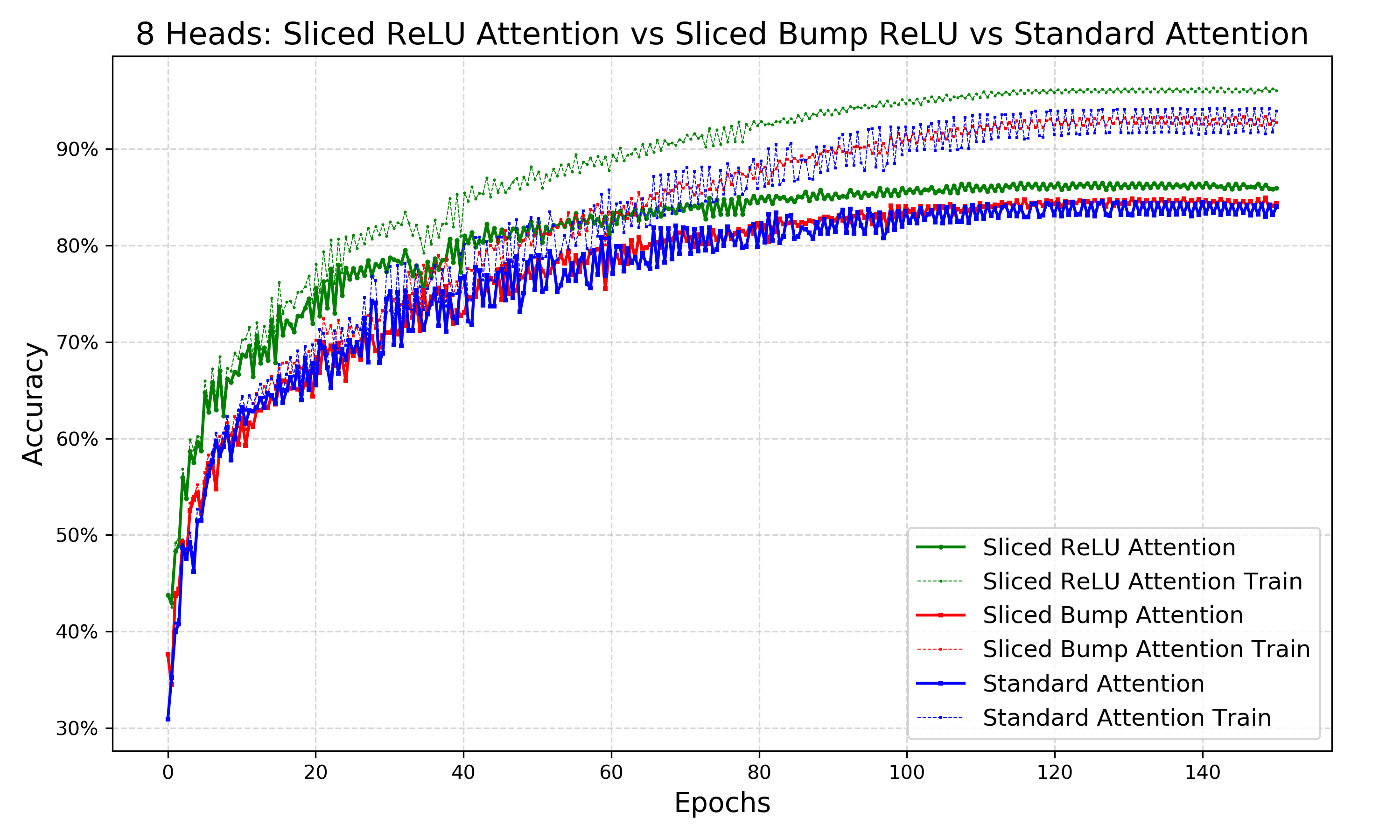
Figure 2: On Cifar-10, sliced ReLU-bump and softmax attention perform equally well, and are slightly outperformed by Sliced ReLU.

Implications and Future Directions

The implications of the sliced ReLU attention mechanism are both practical and theoretical. On the practical side, it enables efficient processing of long contexts, crucial for applications such as document-level understanding or high-resolution imaging. Theoretically, it pushes toward understanding and optimizing attention mechanisms beyond softmax, potentially leading to more efficient and expressive architectures.

Future work could explore scaling the model to larger tasks or contexts, leveraging the computational efficiency for broader applications in multimodal settings or generative tasks. Additionally, refining the model training dynamics could bridge the gap between empirical performance and theoretical capabilities, further establishing sliced ReLU attention as a robust alternative to traditional attention mechanisms.

Conclusion

"Sliced ReLU attention: Quasi-linear contextual expressivity via sorting" proposes an innovative approach to attention mechanisms, leveraging computational efficiency through sorting while retaining the theoretical expressivity of softmax attention. Through rigorous theoretical analysis and empirical validation, sliced ReLU attention emerges as a promising solution for handling long contexts efficiently in various machine learning tasks. The exploration of this mechanism indicates potential avenues for further research and optimization in attention-based architectures.