- The paper introduces HAGeo, a system that uses heuristic auxiliary constructions to achieve gold-medal performance on IMO benchmarks.
- It employs a DDAR engine and numerical geometric deductions, yielding a 20x speedup over neural network-based methods.
- Evaluations on IMO-30 and HAGeo-409 benchmarks validate the framework’s robustness and practical impact in automated geometry solving.
Gold-Medal-Level Olympiad Geometry Solving with Efficient Heuristic Auxiliary Constructions
Introduction
The paper "Gold-Medal-Level Olympiad Geometry Solving with Efficient Heuristic Auxiliary Constructions" (2512.00097) presents HAGeo, a novel system for automated theorem proving in Euclidean geometry targeting IMO-level problems. Unlike previous approaches, HAGeo operates entirely on CPUs without relying on neural networks. HAGeo achieves superior performance compared to the neural network-intensive AlphaGeometry by utilizing a heuristic-based method to add auxiliary constructions, reaching "gold-medal" performance by solving 28 out of 30 problems on the IMO-30 benchmark.
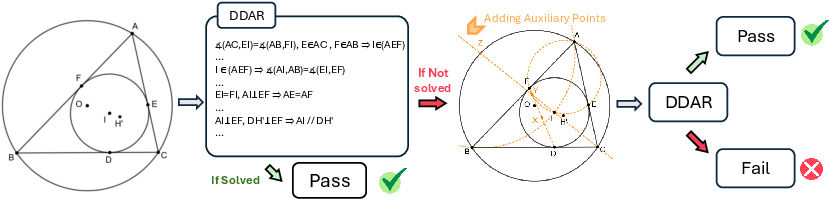
Figure 1: Overview of the HAGeo method, combining a DDAR engine with heuristic strategies for efficient problem-solving.
Methodology
The proposed approach is grounded in a heuristic framework for identifying and introducing auxiliary points. These points are strategically selected based on geometric properties (like intersections of lines and circles) deduced through numerical calculations. This facilitates the deduction process for complex geometric problems without resorting to computationally expensive neural network models.
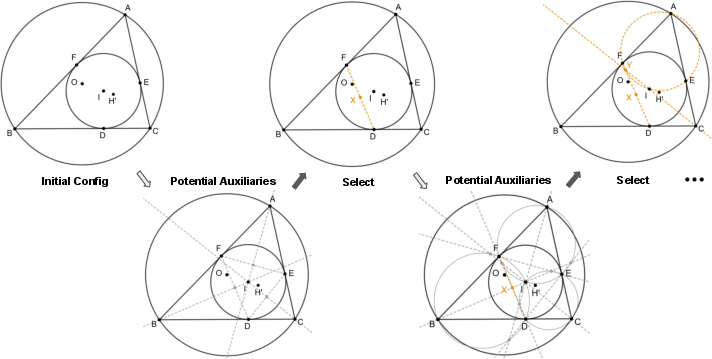
Figure 2: Pipeline illustrating the procedure for adding heuristic auxiliary points through algebraic and geometric computation.
HAGeo incorporates an optimized Deductive Database and Algebraic Reasoning (DDAR) engine that significantly enhances performance while reducing computational overhead. By refining deduction rules, it achieves a notably faster inference speed, running approximately 20 times faster than comparable neural-symbolic systems like AlphaGeometry. This speedup is critical for handling larger benchmarks such as HAGeo-409, consisting of 409 problems with assessed difficulty levels.
Benchmarking and Evaluation
The performance of HAGeo was assessed against existing methods using two benchmarks: the traditional IMO-30 and the newly introduced HAGeo-409. The latter provides a more challenging and comprehensive evaluation framework than IMO-30 by including problems with higher difficulty ratings.
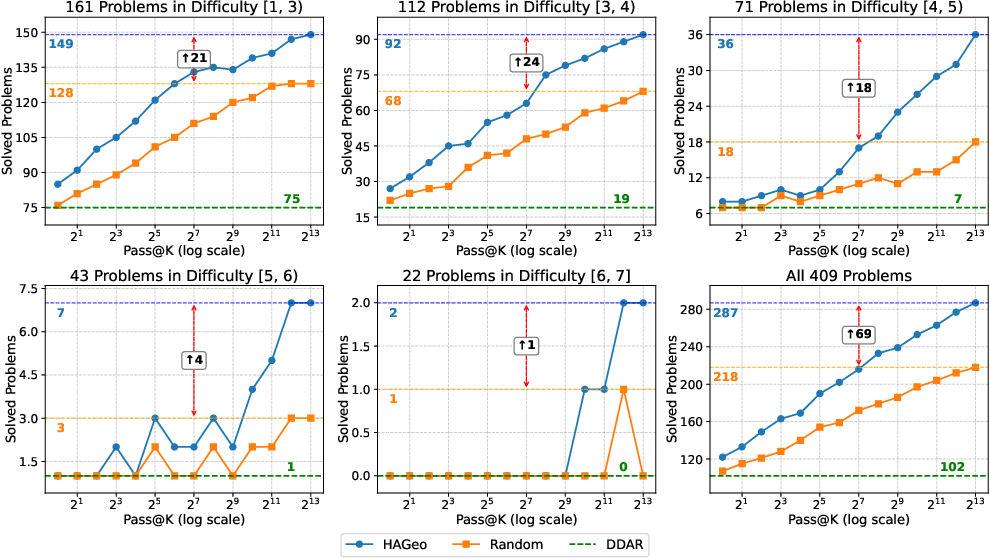
Figure 3: Pass@K results of HAGeo versus random DDAR baselines on HAGeo-409, highlighting the performance across various difficulty tiers.
In comparison, while AlphaGeometry and analogous neural models rely heavily on GPU-driven inference for performance, HAGeo, using solely heuristic strategies, matches and surpasses these methods in efficiency and problem-solving capability. Experimentation on the HAGeo-409 benchmark further underlines HAGeo's robustness, successfully tackling more intricate problems that typically pose challenges for traditional benchmarks.
Implications and Future Directions
Practically, HAGeo offers a viable alternative avenue for automated theorem proving in geometry without the computational demands associated with neural networks. Theoretically, it underscores the merit of heuristic-driven methodologies in automated reasoning, showing that strategic point construction can bridge the solution gap left by algebraic and deductive techniques alone.
The insights gained from developing HAGeo pave the way for further exploration into heuristic augmentation techniques, not only in geometry but potentially across different mathematical domains amenable to similar methodologies. Future work could explore enhancing the heuristic-based construction framework to cover broader and increasingly complex problem sets, facilitating even greater automation in mathematical reasoning tasks.
Conclusion
HAGeo represents a significant step towards efficient and effective automated theorem proving in geometry, highlighting the potential of heuristic-based approaches. By achieving gold-medal level performance on the IMO-30 benchmark and outperforming existing neural network-based methods, HAGeo sets a new standard for computational geometry solving frameworks. The introduction of the HAGeo-409 benchmark further strengthens its positioning as a comprehensive tool for the advancement of automated problem-solving in mathematics.




