SR-Scientist: Scientific Equation Discovery With Agentic AI (2510.11661v1)
Abstract: Recently, LLMs have been applied to scientific equation discovery, leveraging their embedded scientific knowledge for hypothesis generation. However, current methods typically confine LLMs to the role of an equation proposer within search algorithms like genetic programming. In this paper, we present SR-Scientist, a framework that elevates the LLM from a simple equation proposer to an autonomous AI scientist that writes code to analyze data, implements the equation as code, submits it for evaluation, and optimizes the equation based on experimental feedback. Specifically, we wrap the code interpreter into a set of tools for data analysis and equation evaluation. The agent is instructed to optimize the equation by utilizing these tools over a long horizon with minimal human-defined pipelines. Empirical results show that SR-Scientist outperforms baseline methods by an absolute margin of 6% to 35% on datasets covering four science disciplines. Additionally, we demonstrate our method's robustness to noise, the generalization of the discovered equations to out-of-domain data, and their symbolic accuracy. Furthermore, we develop an end-to-end reinforcement learning framework to enhance the agent's capabilities.
Sponsored by Paperpile, the PDF & BibTeX manager trusted by top AI labs.
Get 30 days freePaper Prompts
Sign up for free to create and run prompts on this paper using GPT-5.
Top Community Prompts
Explain it Like I'm 14
What is this paper about?
This paper introduces SR-Scientist, an AI system that acts like a small “digital scientist.” Its job is to discover the math equations that best explain data from science (like physics or chemistry). Unlike past methods where AI just suggests equations, SR-Scientist can write and run code to analyze data, test equations, see what works, and improve its ideas over many steps—all with minimal human instructions.
What questions were they trying to answer?
- Can we make an AI that doesn’t just guess equations, but also tests and improves them on its own—like a scientist?
- Will this “agent” approach discover better, simpler, and more accurate equations than existing methods?
- Can the AI’s discovered equations handle noisy data and still work well on new, unseen data?
- Can we train this AI to get even better over time using feedback (a form of practice called reinforcement learning)?
How did they do it?
The core idea: symbolic regression
Symbolic regression is a fancy name for “finding the math rule that explains how inputs lead to outputs.” Imagine you watch a bouncing ball and record its height over time. Symbolic regression tries to find a clean equation (like height = something involving time and gravity) that matches those measurements.
This is hard because there are countless possible equations. SR-Scientist uses a powerful LLM (an AI that understands and writes text and code) to explore this huge space more intelligently.
Turning an AI into a “scientist”
Most previous AI systems only propose equations. SR-Scientist goes further. It:
- Thinks about the problem and sets a precision goal (how accurate it wants to be).
- Writes code to analyze the data (to spot patterns).
- Writes code to test candidate equations on the data.
- Gets feedback (how well the equation fits).
- Improves the equation and tries again, multiple times.
This “think–act–learn” loop can run for many steps (called “long-horizon optimization”), just like a scientist refining a hypothesis.
Tools the AI uses (explained with simple analogies)
SR-Scientist has two main “lab tools” it can call by writing code:
- Data analyzer (T1): Like looking at your experiment notebook with a calculator. It prints the data, computes averages, checks correlations, and studies “residuals” (the differences between predicted values and the real ones), so the AI can see where its equation is off.
- Equation evaluator (T2): Like a test bench for equations. The AI provides an equation with placeholders for unknown constants (like a, b, c), and the tool uses an optimizer (called BFGS—think “automatic knob-tuner”) to find the best values for those constants and reports how well the equation fits.
To measure accuracy, the system uses MAPE (Mean Absolute Percentage Error). In plain terms, MAPE is the average percentage difference between the AI’s predictions and the true values. Lower is better.
Learning from experience (the “experience buffer”)
Since the AI can only remember so much in one go, SR-Scientist keeps a “notebook” (an experience buffer) of the best equations it has tried and how well they performed. In the next round, it reuses the best past ideas as examples—just like a student reuses good solutions when solving new tasks.
Reinforcement learning (practice with feedback)
The authors also train the AI end-to-end with reinforcement learning (RL). You can think of RL as practice: the AI tries equations, gets a score based on how close they are to the data, and is rewarded for better fits. Over time, this helps the AI improve its “scientist skills.” They use a method called GRPO (Group Relative Policy Optimization) to guide this practice more efficiently.
What did they find?
Here are the main results in simple terms:
- SR-Scientist beats previous equation-finding methods by a noticeable margin. Across four science areas (physics, chemistry, biology, materials), it improved results by about 6% to 35% compared to strong baselines.
- It works well with different backbone AI models (they tried several). The best setup achieved strong accuracy even at strict precision levels.
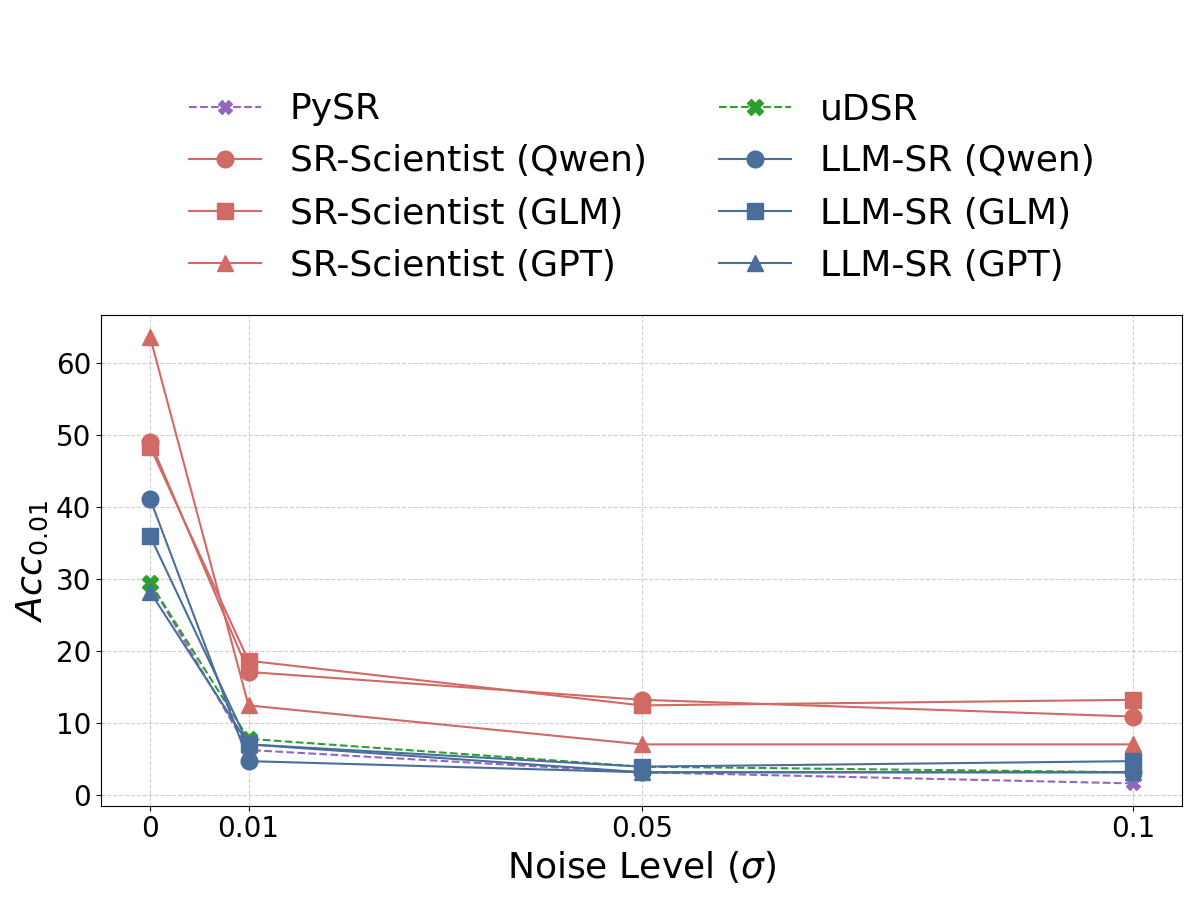
- It holds up under noisy data. When the input measurements were “wiggly” (random noise added), SR-Scientist still performed better than others.
- It generalizes to new situations. Equations discovered by SR-Scientist often still worked on new data from slightly different conditions (called out-of-domain data), which is important in real science.
- It more often finds the exact same equation form as the hidden ground truth (this is called symbolic accuracy). That’s a big deal because it means the AI isn’t just fitting numbers—it’s rediscovering the true underlying relationship.
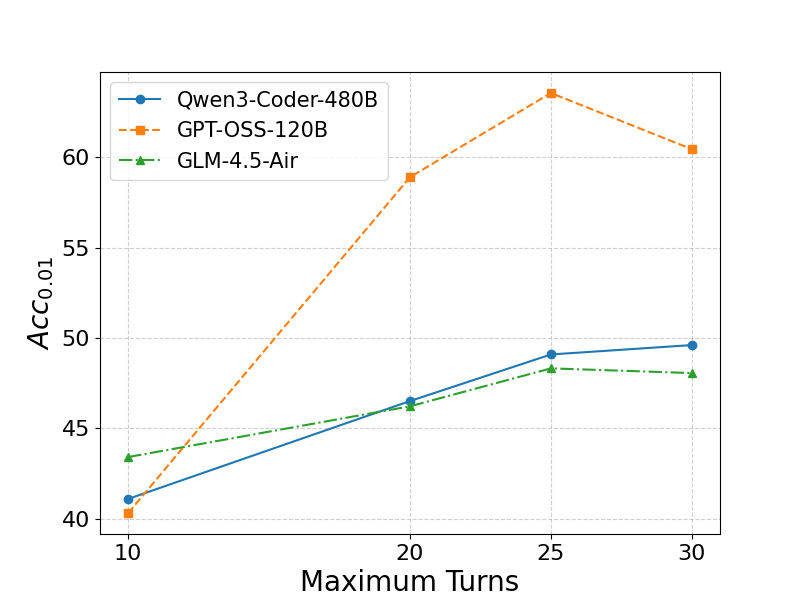
- Long-horizon thinking matters. Allowing the AI more steps per attempt (up to around 25) improved performance. Too few steps limited learning; too many didn’t help much.
- The special pieces matter. Removing the data analyzer tool or the experience buffer made the system worse. This shows both analysis and memory are key.
- RL training helps. Training the agent with feedback improved its abilities, even on different model backbones.
Why does it matter?
- Speeds up discovery: Scientists often spend a lot of time testing equations and checking fits. An AI that can autonomously analyze data, propose equations, and refine them can accelerate research.
- Better understanding: Equations are compact, interpretable “explanations” of how things work. Finding them helps us understand the world, not just predict it.
- Robust to real-world messiness: The system’s ability to handle noisy data and new conditions makes it more useful outside the lab, where measurements are rarely perfect.
- Learns over time: Because the AI improves with practice (RL) and keeps a memory of good ideas (the buffer), it can evolve into a more capable “digital scientist.”
- Broad impact: This approach could help in physics (motion, energy), chemistry (reaction rates), biology (growth patterns), and materials (strength vs. composition), and even in engineering or environmental science, wherever equations matter.
In short, SR-Scientist shows that giving an AI the tools and freedom to think, test, and learn—like a scientist—can lead to better, more reliable equation discovery. This could make scientific research faster, more precise, and more accessible.
Knowledge Gaps
Knowledge gaps, limitations, and open questions
The following list captures what remains missing, uncertain, or unexplored in the paper and can guide concrete follow-up research:
- Lack of evaluation on real-world experimental datasets; results are confined to synthetic benchmarks (LSR-Synth), leaving external validity uncertain.
- The framework targets scalar-output symbolic regression; handling of multi-output systems, coupled equations, implicit equations, and PDEs remains unaddressed.
- No enforcement or explicit modeling of physical constraints (e.g., dimensional consistency, unit correctness, positivity of physical constants), risking physically invalid yet accurate equations.
- Optimization objective mismatch: training/goal uses MAPE, final selection sometimes uses NMSE, and reporting uses accuracy-to-tolerance—impact of these mismatches on search dynamics and generalization is not quantified.
- MAPE can be unstable with near-zero targets; safeguards, transformations, or alternative metrics for zero-inflated or sign-changing data are not discussed.
- Model selection uses the best-performing equation on the training/observed data; no validation set or correction for multiple comparisons is used, increasing overfitting risk.
- No explicit complexity/interpretability control (e.g., MDL or Pareto error–complexity trade-offs); complexity of discovered equations and its effect on generalization/interpretability are not analyzed.
- Constant fitting relies on BFGS with unspecified initialization and no multi-start/global strategies; susceptibility to local minima and its impact on outcomes are not studied.
- Constraints on constants (e.g., positivity, bounds) are not enforced during fitting, even though such constraints are common in scientific laws.
- Numerical stability safeguards (e.g., domain restrictions to avoid division by near-zero, overflow in exponentials/logs) are not described; robustness to numerical pathologies is untested.
- Experience buffer retrieves top-K equations by error only; diversity-aware memory, novelty search, or anti-mode-collapse strategies are not explored.
- Sensitivity to experience buffer hyperparameters (buffer size, K, ranking criteria) and their influence on exploration–exploitation balance is not provided.
- The UpdateGoal(H, G_i) schedule, stopping thresholds, and goal adaptation logic are unspecified; their effect on convergence and performance remains unclear.
- Training rollouts restrict to a single iteration, whereas inference uses long-horizon multi-iteration optimization; this train–test mismatch leaves credit assignment across long tool-use trajectories underexplored.
- Reward shaping is fixed (log-linear with s_max and s_goal) without sensitivity analyses; risks of reward hacking and the balance between structure discovery vs. constant tuning are not quantified.
- GRPO is trained without a KL penalty; stability, potential mode collapse, and side effects on general coding/reasoning abilities are not evaluated.
- RL training is demonstrated primarily on one backbone (Qwen3-Coder-30B) due to infra limits; scalability of RL benefits across model sizes and families is not systematically established.
- Compute, runtime, and energy costs (LLM calls, tool invocations, code execution time) are not reported; fairness of resource budgets vs. baselines is unclear.
- Baseline parity: limiting non-LLM methods to 100k candidates and LLM methods to 1k calls may not equate computational budgets; no sensitivity to budget scaling is provided.
- OOD behavior (e.g., material science improving from ID to OOD) is observed but not explained; the factors driving domain-specific generalization patterns remain open.
- Noise robustness tested only with i.i.d. Gaussian noise added to training data; effects of heteroscedastic noise, heavy tails, outliers, missing data, and test-time noise are not explored.
- Toolset is minimal (data analyzer, evaluator); absence of domain-prior tools (unit/dimensional analysis, constraint checkers, ODE/PDE solvers, simulators) may limit discovery of mechanistic equations.
- Operator set, grammar, and expression space are not clearly specified; rates of unparsable/invalid equations and their filtering strategies are not reported.
- Error-handling and reliability of code execution (frequency of failures, recovery policies, proportion of wasted calls) are not measured.
- Failure mode analysis is limited; systematic characterization of common agent errors (e.g., hallucinated code, repetitive exploration, brittle reliance on specific analyses) is missing.
- Human-centered interpretability is not assessed; no human studies on equation readability, scientific plausibility, or usefulness to domain experts.
- Symbolic accuracy remains low overall; strategies to directly reward structure-level correctness (e.g., tree-edit rewards, canonicalization-aware objectives) are not investigated.
- Hyperparameter sensitivity beyond max turns (e.g., iterations N, K, buffer size, MAPE targets, BFGS settings) is not reported.
- Scalability with input dimensionality (number of variables, feature correlations) is not evaluated; upper bounds on problem size remain unknown.
- Potential pretraining leakage is only qualitatively addressed; no systematic audit or memorization tests (e.g., counterfactual benchmarks, watermarking) are provided.
- Tool-usage analyses rely on LLM-based classification of tool calls; no human validation of these labels, nor correlation between tool-use patterns and performance, is presented.
- Statistical uncertainty is underreported (only means over three runs); standard deviations, confidence intervals, and significance tests are absent.
- Post-RL side effects on broader capabilities (coding reliability, math reasoning, general alignment) are not measured, raising questions about catastrophic forgetting or behavioral drift.
- Security and reproducibility of code execution (sandboxing, deterministic seeds, environment specs) are not detailed; exact prompts/trajectories for replication are not fully specified.
Practical Applications
Immediate Applications
Below are applications that can be deployed now using the SR-Scientist framework and its released tools and models.
- Agent-augmented symbolic regression in scientific R&D (materials, chemistry, biology, physics)
— Tools/products: Jupyter/VSCode extensions that wrap the data analyzer (
T1) and equation evaluator (T2), using BFGS for constant fitting and the experience buffer for long-horizon optimization. — Assumptions/Dependencies: Clean, well-curated datasets; sandboxed code execution; sufficient compute; domain-aware prompts to avoid trivial memorization; acceptance criteria aligned with MAPE/NMSE targets. - Interpretable surrogate modeling for simulation and design (energy, manufacturing, aerospace, automotive)
— Use cases: Replace or complement high-fidelity simulations (COMSOL, ANSYS, CFD/FEA) with interpretable equations for rapid design space exploration and sensitivity analysis.
— Assumptions/Dependencies: Integration adapters to CAE tools; unit/dimension sanity checking; validated out-of-domain (OOD) performance and tolerance thresholds (e.g.,
Acc_0.01). - Offline system identification for control and robotics (robotics, industrial automation) — Use cases: Derive transfer functions or nonlinear dynamics from logged trajectories; residual analysis to refine models; faster controller prototyping with interpretable equations. — Assumptions/Dependencies: Adequate sampling rates and coverage; noise robustness settings; offline pipeline (real-time inference not guaranteed); safety reviews before deployment.
- Model auditing and compression for ML pipelines (software, healthcare, life sciences) — Use cases: Fit symbolic approximations to black-box predictors to gain interpretability, stress-test generalization, and identify spurious features; produce compliance-ready documentation. — Assumptions/Dependencies: Careful OOD validation; regulatory constraints (e.g., clinical validation); disclosure of training data, reward design, and evaluation metrics.
- Process optimization and monitoring from sensor data (process industries, energy, utilities) — Use cases: Discover equations linking operational variables (flow, temperature, energy consumption) for anomaly detection and predictive maintenance; set interpretable KPI triggers via residuals. — Assumptions/Dependencies: Sensor calibration and drift handling; noise-aware fitting (parameter σ); clear operational tolerance definitions; ongoing recalibration workflows.
- Education and citizen science (education, consumer electronics) — Use cases: Classroom labs where students collect data and “rediscover” governing laws; maker/citizen-science kits to fit equations to environmental or motion sensor data. — Assumptions/Dependencies: Simplified UI; safe tool execution; curated datasets to avoid misinterpretation; scaffolded instructional prompts.
- Data science pipeline integration (software engineering)
— Tools/products: A scikit-learn–style estimator, e.g.,
SRScientistRegressor, wrapping long-horizon ReAct flow,T1/T2tools, and experience buffer; CLI integration (Gemini CLI, Claude Code). — Assumptions/Dependencies: Python runtime stability; library whitelisting; reproducible seeds; budgeted LLM calls (e.g., ≤1,000 per job) and turn limits (e.g., ≤25). - Benchmarking and RL fine-tuning of agentic models (academia, ML ops)
— Use cases: Adopt GRPO-based training with continuous rewards (MAPE goals) to tailor SR-Scientist to domain-specific datasets; build internal SR benchmarks for team workflows.
— Assumptions/Dependencies: Synthetic/curated training data generation; reward design tuning (
s_max,s_goal); compute availability; drift monitoring between training and deployment domains.
Long-Term Applications
Below are applications that will benefit from further research, scaling, or development (e.g., stronger toolchains, formal guarantees, or integrated lab automation).
- Autonomous AI scientists for closed-loop experimentation (academia, pharma/chemistry labs, advanced materials) — Use cases: Propose experiments, collect data via lab robotics, refine equations over long horizons, and manage experience buffers across campaigns. — Assumptions/Dependencies: Robotic instrumentation integration (LIMS/ELN), safety protocols, experiment-cost optimization, robust task decomposition beyond fixed pipelines.
- Discovery of new physical, biological, and chemical laws (academia, deep-tech startups) — Use cases: Hypothesis generation in domains where governing equations are unknown or partially specified; uncover novel terms that generalize across regimes. — Assumptions/Dependencies: High-diversity, high-quality data; domain constraints (units, conservation laws) embedded into tooling; rigorous peer review and replication.
- Interpretable digital twins at scale (energy grids, manufacturing lines, climate/earth systems) — Use cases: Maintain twins built from symbolic models that adapt to distribution shifts; support root-cause analysis and scenario planning. — Assumptions/Dependencies: Streaming data ingestion; change-point detection; governance frameworks for updates; hybrid modeling with physics-informed constraints.
- Safety-critical system assurance with formal guarantees (aviation, medical devices, autonomous vehicles) — Use cases: Combine SR-Scientist with unit-aware dimension analysis, theorem provers, and formal verification to certify dynamics and control equations. — Assumptions/Dependencies: Verified toolchain; standards-compliant documentation; integration with formal methods; strict acceptance metrics beyond MAPE (e.g., stability margins).
- Regulatory standards for AI-discovered scientific models (policy, regulatory science)
— Use cases: Define transparency requirements for equation discovery (tools invoked, reward functions, datasets); establish validation criteria (e.g.,
Acc_τthresholds, OOD stress tests). — Assumptions/Dependencies: Multi-stakeholder consensus; sector-specific guidelines (healthcare, energy); reproducibility checklists and audit trails. - Equation knowledge bases and marketplaces (software platforms, open science) — Use cases: Curate and distribute discovered equations with metadata, OOD performance, and symbolic accuracy; enable reuse across sectors (“EquationHub”). — Assumptions/Dependencies: Licensing and attribution; quality control workflows; schema for provenance and experimental context; community moderation.
- Multi-agent collaborative discovery (software, academia) — Use cases: Specialized agents for data analysis, equation evaluation, literature synthesis, and concept libraries working in concert; pooled experience buffers across projects. — Assumptions/Dependencies: Coordination protocols, shared memory and retrieval systems, privacy controls; robust long-horizon planning under budget constraints.
- Interpretable financial and macroeconomic modeling (finance, policy analysis) — Use cases: Discover constrained, interpretable alphas or macro relationships; stress-test OOD robustness and avoid spurious solutions. — Assumptions/Dependencies: Strict backtesting and leakage prevention; compliance and risk controls; domain-specific priors and constraints; realistic data-generating assumptions.
Glossary
- Ablation paper: A controlled analysis where components of a system are removed to assess their impact on performance. "our ablation studies highlight the importance of data analysis, the experience buffer, and long-horizon optimization."
- Accuracy-to-tolerance: An evaluation metric that checks whether prediction errors stay within a specified relative tolerance across test points. "We use accuracy-to-tolerance as our main metric."
- Agentic AI: AI systems that autonomously plan, act, and adapt in pursuit of goals by interacting with their environment. "Agentic AI can autonomously execute complex tasks in dynamic environments requiring adaptation, interaction, and reasoning in a goal-oriented manner~\citep{schneider2025generativeagenticaisurvey}."
- BFGS algorithm: A quasi-Newton optimization algorithm used to fit continuous parameters efficiently. "During the execution phase, the BFGS algorithm is implemented to optimize these constants and then report the performance of the equation."
- Code interpreter: An execution tool that lets the agent write and run code for analysis and evaluation. "We provide a code interpreter as the primary tool, enabling the agent to write code for data analysis and performance evaluation."
- Combinatorial search: A search strategy over discrete structures (e.g., expressions) that explores combinations of elements to find high-performing solutions. "Traditional methods have relied on Genetic Programming (GP) for combinatorial search~\citep{cranmer2023interpretablemachinelearningscience}."
- Data analyzer: A tool wrapper around the code interpreter that enables programmatic data exploration and statistics. "we wrap the code interpreter into two common tools for the tasks, data analyzer and equation evaluator, denoted as and , respectively."
- Equation evaluator: A tool that evaluates candidate symbolic equations (with constants) against data, optimizing constants if needed. "For , following the approach of \citet{shojaee2025llmsrscientificequationdiscovery}, we design the tool to accept an equation skeleton with placeholders for constants in code format."
- Equation skeleton: A symbolic expression template with placeholders for constants to be fitted. "we design the tool to accept an equation skeleton with placeholders for constants in code format"
- Experience buffer: A memory of past candidate equations and their scores used to guide future iterations. "we implement an experience buffer to fetch the best-performing equations for subsequent iterations."
- Expression trees: Tree-structured representations of symbolic expressions used to define and search over expression spaces. "This line of methods uses constrained representations, such as expression trees, to define a search space composed of symbolic operators, constants, and variables~\citep{cranmer2023interpretablemachinelearningscience}."
- Gaussian noise: Random noise drawn from a normal distribution added to data to test robustness. "we add Gaussian noise with different standard deviations () to each training data point"
- Genetic Programming (GP): An evolutionary algorithm framework that evolves symbolic programs or expressions to optimize performance. "Traditional methods have relied on Genetic Programming (GP) for combinatorial search~\citep{cranmer2023interpretablemachinelearningscience}"
- Group Relative Policy Optimization (GRPO): A policy-gradient RL algorithm that optimizes policies using group-wise relative advantages. "We apply the Group Relative Policy Optimization (GRPO) ~\citep{shao2024deepseekmathpushinglimitsmathematical} algorithm for optimization."
- In-context examples: Previously found high-performing solutions provided in the prompt to steer the model’s generation. "we fetch the best equations from the buffer and provide them to the agent as in-context examples."
- In-domain (ID): Test data drawn from the same distribution as the training data. "a training set accessible to the SR method, an in-domain (ID) test set, and an out-of-domain (OOD) test set."
- KL penalty: A regularization term penalizing divergence from a reference policy during RL training. "To encourage exploration, we omit the KL penalty term against a reference model and observe that this leads to faster convergence and comparable performance."
- Long-horizon optimization: Multi-step reasoning and tool use over many interactions to iteratively improve solutions. "At each iteration, the LLM agent autonomously conducts long-horizon optimization using code interpreters for data analysis and equation evaluation."
- Mean Absolute Percentage Error (MAPE): A percentage-based error metric measuring average relative deviation between predictions and ground truth. "We choose the mean absolute percentage error (MAPE) as the goal"
- Mean Squared Error (MSE): An error metric measuring the average of squared prediction errors. "other SR methods that usually use the mean squared error (MSE) or normalized mean squared error (NMSE) as the score"
- Normalized Mean Squared Error (NMSE): A scale-invariant version of MSE that normalizes error, often by variance. "other SR methods that usually use the mean squared error (MSE) or normalized mean squared error (NMSE) as the score"
- Out-of-domain (OOD): Test data drawn from a distribution different from the training data to assess generalization. "a training set accessible to the SR method, an in-domain (ID) test set, and an out-of-domain (OOD) test set."
- ReAct framework: A prompting paradigm that interleaves reasoning (thoughts) and actions (tool calls) with feedback. "the agent's trajectory is structured as follows, typically within a ReAct~\citep{yao2023reactsynergizingreasoningacting} framework:"
- Reinforcement learning (RL): A learning paradigm where an agent optimizes behavior via rewards from interactions with an environment. "we develop an end-to-end reinforcement learning framework to enhance the agent's capabilities."
- Residuals: Differences between predicted and true values used to analyze model fit and error patterns. "or analyzing the residuals between the predicted value and the true value."
- Reward function (log-linear): A mapping from performance metrics to scalar rewards using a logarithmic-linear form. "We employ a log-linear reward function that maps to the range as follows:"
- Reward sparsity: A problem in RL where informative rewards are rare or zero for most behaviors. "This makes it possible to assign continuous rewards to avoid reward sparsity."
- Rollout: The process of executing the agent’s policy in the environment to collect trajectories and rewards. "During rollout, we set the maximum number of turns to 20 and train for 60 steps."
- Symbolic accuracy: A metric that checks whether a discovered equation matches the ground-truth expression exactly. "Additionally, we present symbolic accuracy, which checks if the discovered equations are identical to the ground truth equations."
- Symbolic regression (SR): The task of discovering interpretable symbolic expressions that fit observed data. "The task of data-driven equation discovery, also known as symbolic regression (SR), is an NP-hard problem due to its vast search space~\citep{virgolin2022symbolicregressionnphard}."
- Trajectory (agent): The sequence of thoughts, tool calls, and observations produced by the agent during problem solving. "the agent's trajectory is structured as follows, typically within a ReAct~\citep{yao2023reactsynergizingreasoningacting} framework:"
Collections
Sign up for free to add this paper to one or more collections.