2000 character limit reached
Coevolutionary Continuous Discrete Diffusion: Make Your Diffusion Language Model a Latent Reasoner (2510.03206v1)
Published 3 Oct 2025 in cs.AI and cs.CL
Abstract: Diffusion LLMs, especially masked discrete diffusion models, have achieved great success recently. While there are some theoretical and primary empirical results showing the advantages of latent reasoning with looped transformers or continuous chain-of-thoughts, continuous diffusion models typically underperform their discrete counterparts. In this paper, we argue that diffusion LLMs do not necessarily need to be in the discrete space. In particular, we prove that continuous diffusion models have stronger expressivity than discrete diffusions and looped transformers. We attribute the contradiction between the theoretical expressiveness and empirical performance to their practical trainability: while continuous diffusion provides intermediate supervision that looped transformers lack, they introduce additional difficulty decoding tokens into the discrete token space from the continuous representation space. We therefore propose Coevolutionary Continuous Discrete Diffusion (CCDD), which defines a joint multimodal diffusion process on the union of a continuous representation space and a discrete token space, leveraging a single model to simultaneously denoise in the joint space. By combining two modalities, CCDD is expressive with rich semantics in the latent space, as well as good trainability and sample quality with the help of explicit discrete tokens. We also propose effective architectures and advanced training/sampling techniques for CCDD, which reveals strong empirical performance in extensive LLMing experiments on real-world tasks.
Summary
- The paper introduces CCDD, which unifies continuous and discrete diffusion processes to improve latent reasoning in language models.
- It employs a joint denoising approach with modality-specific heads, combining CTMC for tokens and SDE for embeddings to balance expressivity and decodability.
- Empirical results demonstrate over 25% perplexity reduction on LM1B and enhanced efficiency via classifier-free guidance and asynchronous noise schedules.
Coevolutionary Continuous Discrete Diffusion: A Unified Paradigm for Latent Reasoning in Diffusion LLMs
Introduction and Motivation
The paper introduces Coevolutionary Continuous Discrete Diffusion (CCDD), a novel LLMing framework that unifies continuous and discrete diffusion processes to address the limitations of existing diffusion LLMs (DLMs) and looped transformers (LTs). The motivation stems from a fundamental contradiction: while continuous diffusion models (CDMs) are theoretically more expressive than discrete diffusion models (DDMs) and LTs, they underperform in practice due to trainability and decoding challenges. CCDD is designed to bridge this gap by coevolving both modalities, leveraging the semantic richness of continuous representations and the decodability of discrete tokens.
Theoretical Analysis: Expressivity and Trainability
The paper provides a rigorous theoretical comparison of DDMs, CDMs, and LTs in terms of expressivity and trainability.
- Expressivity: CDMs are shown to strictly dominate DDMs and LTs at the trajectory level. The continuous state in CDMs retains fine-grained uncertainty and historical memory, while DDMs quantize information at each step, incurring information loss. CDMs can simulate LTs by discretizing the reverse ODE, but the converse does not hold for stochastic CDMs.
Figure 1: Comparison of theoretical expressiveness and practical trainability of: discrete diffusion (left), continuous diffusion with optional continuous noise (middle), and looped transformer (right).
- Trainability: Despite their expressivity, CDMs are harder to train due to the high-dimensional, unconstrained generation space and the combinatorial complexity of decoding continuous latents to discrete tokens. LTs suffer from out-of-distribution (OOD) issues due to lack of intermediate supervision. DDMs, while less expressive, are easier to optimize and decode.
The analysis concludes that the practical performance gap is rooted in the trade-off between expressivity and trainability, motivating a hybrid approach.
The CCDD Framework: Joint Continuous-Discrete Diffusion
CCDD defines a joint diffusion process over both discrete token space and continuous representation space. The forward process applies independent noise to each modality: a CTMC for discrete tokens and an SDE for continuous embeddings. The reverse process employs a single time-conditioned network that jointly denoises both modalities, with modality-specific heads for prediction.
Figure 2: Framework of Coevolutionary Continuous Discrete Diffusion.
Key features of CCDD include:
- Joint Denoising: The model conditions on both noisy tokens and representations, enabling cross-modal information flow and improved denoising.
- Intermediate Supervision: Both modalities are supervised at all timesteps, mitigating OOD issues and facilitating flexible inference-time scaling.
- Expressivity and Decodability: The continuous component enhances expressivity and semantic richness, while the discrete component anchors the model to decodable outputs, reducing ambiguity.
Implementation: Architectures and Training Techniques
The paper explores several architectural instantiations for CCDD, inspired by DiT, MM-DiT, and MoE paradigms. These architectures balance parameter efficiency and cross-modal interaction:
Figure 3: Comparison of different denoising network architectures for CCDD.
- MDiT: Standard DiT with mixed continuous and discrete embeddings.
- MMDiT: Multimodal DiT with staggered cross-attention and self-attention blocks.
- MoEDiT: MoE-based DiT with shared attention and modality-specific MLPs, allowing dynamic expert selection.
Representation Selection: The continuous space is instantiated using contextualized embeddings from pretrained LLM encoders (e.g., Qwen3-Embedding). This choice is empirically validated to provide a balance between generativity and decodability, as token-wise embeddings are easier to decode but less expressive, while deep contextualized embeddings are more semantically rich but harder to decode.
Training and Sampling Enhancements:
- Classifier-Free Guidance (CFG): The model is trained with random dropout of continuous embeddings, enabling inference-time guidance by interpolating between conditional and unconditional logits.
- Asynchronous Noise Schedules: The continuous modality is denoised faster than the discrete modality, allowing representations to serve as high-level guidance for token decoding.
- Advanced Sampling: The framework supports both SDE-based high-quality sampling and ODE-based efficient few-step sampling.
Empirical Results
CCDD is evaluated on LM1B and OpenWebText (OWT) benchmarks, using Qwen3-Embedding and RoBERTa as continuous spaces. Key findings include:
- Perplexity Reduction: CCDD achieves over 25% lower validation perplexity on LM1B compared to discrete-only baselines with the same parameter count.
- Scalability: Increasing model parameters and leveraging high-quality embeddings further improve performance.
- Inference Flexibility: CFG and asynchronous schedules enable trade-offs between sample quality and efficiency.
- Ablation Studies: Experiments confirm that deeper contextualized embeddings provide a favorable trade-off between representation MSE and token cross-entropy loss.
Practical and Theoretical Implications
CCDD demonstrates that joint continuous-discrete modeling can overcome the limitations of both CDMs and DDMs. Theoretically, it provides a unified framework that generalizes previous paradigms and achieves strict expressivity gains. Practically, it enables efficient, high-quality LLMing with flexible inference and improved reasoning capabilities.
The approach is compatible with recent advances in representation learning, knowledge distillation, and multimodal generation. The modularity of the framework allows for future extensions, such as integrating additional modalities or leveraging more advanced pretrained representations.
Future Directions
Potential avenues for further research include:
- Scaling to Larger Models and Datasets: Investigating the behavior of CCDD at larger scales and on more diverse corpora.
- Integration with Multimodal Tasks: Extending the framework to handle vision-language or speech-language tasks.
- Theoretical Analysis of Optimization Dynamics: Deeper paper of the optimization landscape and convergence properties in joint diffusion spaces.
- Exploration of Alternative Decoding Strategies: Developing more effective decoders for continuous representations, possibly leveraging energy-based or retrieval-augmented methods.
Conclusion
CCDD provides a principled and practical solution to the expressivity-trainability dilemma in diffusion LLMing. By coevolving continuous and discrete modalities, it achieves strong empirical performance and theoretical guarantees, setting a new direction for latent reasoning in generative LLMs.
Paper Prompts
Sign up for free to create and run prompts on this paper using GPT-5.
Top Community Prompts
Explain it Like I'm 14
Overview
This paper asks a simple question with a big idea behind it: can we make LLMs “think in their head” before choosing words, and do it in a way that’s both powerful and easy to train?
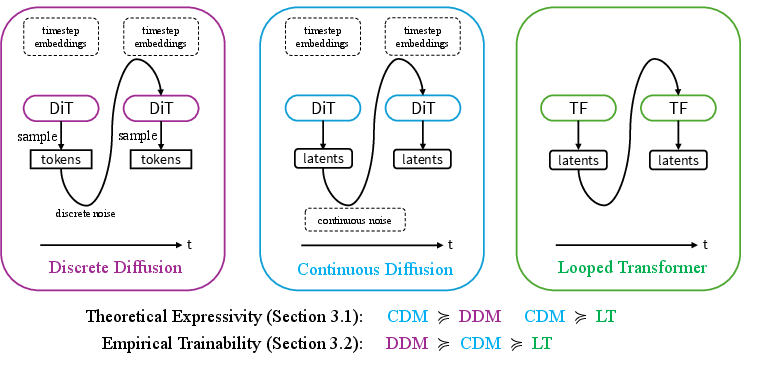
Today’s non-autoregressive LLMs called diffusion LLMs work by starting from noisy text and repeatedly “cleaning it up” until it looks like real text. There are two main flavors:
- Discrete diffusion: works directly with tokens (words/subwords).
- Continuous diffusion: works with continuous vectors (hidden representations) and later turns them into tokens.
The authors show that, in theory, continuous diffusion can think more flexibly than discrete diffusion and a related idea called looped transformers (which reuse the same layers many times). But in practice, continuous models often perform worse because they’re hard to train and hard to turn back into tokens.
Their solution is a new method called CCDD (Coevolutionary Continuous Discrete Diffusion), which lets the model reason in a continuous “thought space” and also keep track of tokens at the same time—so you get the best of both worlds.
Key Objectives
The paper focuses on three main goals:
- Understand which models are theoretically more powerful at representing complex reasoning: continuous diffusion, discrete diffusion, or looped transformers.
- Explain why the models that are more powerful on paper don’t always work best in real life.
- Build a new model (CCDD) that combines continuous and discrete representations so it’s both powerful and practical.
Methods in Plain Language
Here are the core ideas, explained with simple analogies:
- Diffusion as un-blurring:
- Imagine you start with a blurry sentence and sharpen it a little at a time until it becomes clear. That’s diffusion: step-by-step denoising.
- Discrete diffusion sharpens in the world of tokens (like choosing letters/words).
- Continuous diffusion sharpens in the world of vectors (like a mental image of meaning) and later turns that into tokens.
- Why continuous is more expressive:
- Picking a token at each step is like snapping to the nearest word too early—you lose shades of meaning and uncertainty.
- Staying in a continuous “thought space” keeps rich, detailed information across steps, like holding a full mental plan before speaking.
- Why continuous is hard in practice:
- It’s tricky to convert these smooth “thoughts” back into discrete words (decoding).
- The space is larger and more ambiguous, so training can be harder.
- If your vector space is low quality (poor embeddings), generation is choppy or unclear.
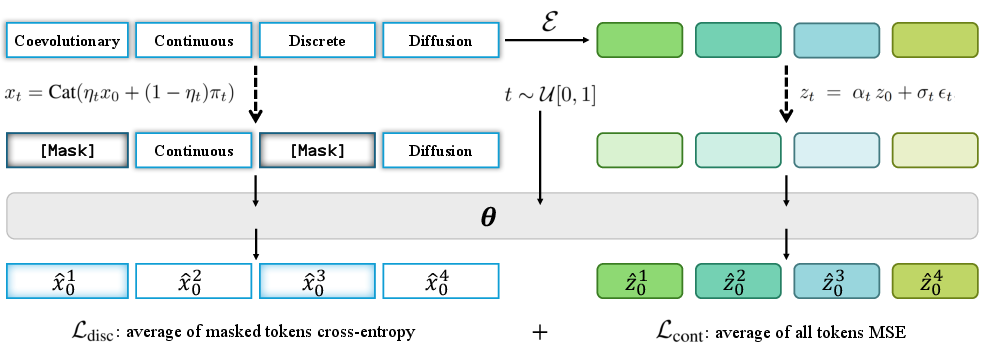
- CCDD: coevolving two views at once
- The model carries two versions of the sentence at every step:
- A continuous version (rich, nuanced, context-aware vectors).
- A discrete version (tokens, which are clear and easy to score).
- During noising (forward) and denoising (reverse), both versions move together. The model sees both and learns to improve both.
- Think of it like planning in your head (continuous) while jotting down key words (discrete) so you don’t get lost. Each helps the other.
- Helpful design choices:
- Use strong, context-aware embeddings from a pretrained text encoder (like Qwen3-Embedding) so the continuous space already “knows” a lot about language.
- Add guidance: treat the continuous side as a kind of “self-guidance” that steers token choices (similar to classifier-free guidance used in image diffusion).
- Asynchronous noise schedules: let the continuous side hold onto information a bit longer so it can guide the tokens more effectively, like forming a plan first and then writing it down.
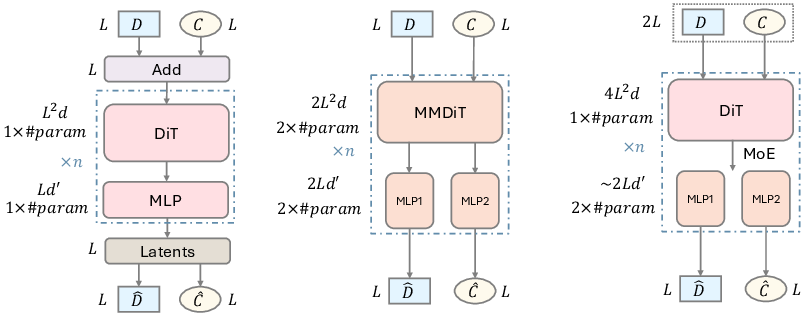
- Architectures: they explore efficient transformer-based designs (MDiT, MMDiT, MoEDiT) to process both views.
Main Findings
- Theory:
- Continuous diffusion can represent a wider range of behaviors than discrete diffusion. In other words, it can carry richer “in-between” information instead of jumping between token choices.
- Continuous diffusion can simulate looped transformers (reusing layers many times), and sometimes do more because it can also handle genuine randomness smoothly.
- Looped transformers often underperform in practice because they aren’t trained on their intermediate steps—so when you “loop” more at test time, you go off-distribution. Diffusion fixes this by training on all steps.
- Practice (experiments):
- On standard language datasets (LM1B and OpenWebText), CCDD beats strong discrete-only baselines.
- Example: on LM1B, CCDD reduces validation perplexity by over 25% compared to a masked discrete diffusion baseline with the same parameter count. Lower perplexity means the model is better at predicting text.
- Using better embeddings (like Qwen3-Embedding) improves performance a lot, because the continuous space carries higher-quality language knowledge.
- Guidance at inference time (using the continuous side to steer tokens) further improves sample quality.
Why This Matters
- Stronger reasoning: Keeping a continuous “inner voice” helps the model plan, explore options, and keep track of uncertainty before committing to words—useful for puzzles, coding, and multi-step logic.
- Better training and decoding: The discrete side acts like sturdy anchor points, making it easier to learn and to turn thoughts into words clearly.
- Flexible and efficient: You can trade speed for quality at inference (fewer or more denoising steps) and use guidance to boost output quality without retraining.
- A unifying path: CCDD blends the strengths of continuous diffusion, discrete diffusion, and looped transformers into a single framework, pointing toward future LLMs that both think well and speak clearly.
In short
CCDD lets a LLM think in rich continuous space and speak in concrete tokens at the same time. This dual view makes it both smarter (more expressive reasoning) and more practical (easier to train and decode), leading to better text generation in real-world tests.
Knowledge Gaps
Knowledge gaps, limitations, and open questions
Below is a concise list of what remains missing, uncertain, or unexplored in the paper, phrased to be actionable for future research.
- Empirical validation of “latent reasoning” claims
- Evaluate CCDD on reasoning-heavy benchmarks (e.g., Sudoku, algorithmic/graph tasks, GSM8K/MATH, planning) and structured/code generation to substantiate claims that continuous latent paths enhance reasoning.
- Factorization choice in the reverse process
- Compare the proposed factored reverse kernels against fully coupled joint kernels to quantify expressivity/quality gaps at finite NFEs and analyze compute–quality trade-offs.
- Forward-process independence assumption
- Investigate coupled forward processes (e.g., shared or correlated noise, co-dependent transition rates) and their impact on learnability and sample quality versus the current independent corruption.
- Representation space selection and alignment
- Systematically paper which encoders, layers, and dimensionalities work best (beyond Qwen3 and a single ablation) and design criteria or automated procedures (e.g., learned adapters) for selecting/combining layers.
- Diagnose and mitigate “out-of-manifold” generation of continuous latents (e.g., manifold regularization, projection layers, contrastive objectives) to ensure generated representations lie on realistic encoder manifolds.
- Decoding alignment and calibration
- Measure calibration and token alignment between continuous latents and discrete predictions (e.g., ECE, coverage), and explore alternative decoders (energy-based, learned decoders, or small LM heads) beyond the Bayes posterior over predicted x0.
- Loss balancing and optimization stability
- Analyze sensitivity to γcont/γdisc and the interaction between losses; develop adaptive or uncertainty-based weighting and gradient-conflict mitigation to prevent one modality dominating or “posterior collapse.”
- Asynchronous noise schedules
- Provide principled design or learning of asynchronous schedules (SNR mismatch) and ablate their effect on planning-like behaviors, convergence, and final quality; investigate schedule adaptation per-sample.
- Representation-based CFG
- Map the quality–diversity frontier under representation CFG (varying pdrop and guidance scale w), diagnose mode collapse, and explore variance-preserving guidance or stochastic guidance alternatives.
- Efficiency and scalability
- Report wall-clock training and inference speed, memory footprint, and throughput versus AR LMs and discrete DLMs under matched hardware; quantify NFE–quality curves and identify regimes where CCDD is latency-competitive.
- Assess scaling to long contexts (8k–32k tokens), large vocabularies, and memory-efficient attention/mixing strategies; characterize degradation rates with length.
- Robustness and OOD generalization
- Test robustness to domain shift, noisy inputs, and adversarial perturbations; quantify self-correction behavior and error recovery compared to masked DDMs and AR LMs.
- Comparative baselines and tokenizer dependence
- Include stronger SOTA discrete DLMs and matched-parameter AR LMs with the same tokenizer, data, and compute; quantify how tokenizer choice confounds perplexity and offer tokenizer-agnostic metrics.
- Conditional tasks and prompting
- Extend CCDD to conditional generation (translation, summarization, instruction following) and specify how both modalities ingest conditions/prompts; compare to AR prompting and DLM conditioning baselines.
- Alignment and human preference optimization
- Integrate preference optimization or RLHF-style objectives for diffusion (e.g., DPO variants) and paper how they affect discrete/continuous heads and CFG/guidance dynamics.
- Theoretical boundaries and assumptions
- Formalize capacity and time-embedding assumptions under which CDMs “simulate” looped transformers, and characterize approximation error bounds in practice.
- Clarify expressivity claims when the continuous space is contextualized, low-dimensional, and non-bijective to tokens; bound what expressivity is lost relative to ideal simplex embeddings.
- Information retention across steps
- Quantify how much historical information the continuous channel preserves (e.g., mutual information across steps) and whether it translates into measurable gains in planning and self-correction.
- Hybrid generation with AR decoding
- Explore hybrids (e.g., CCDD for latent plan, AR for final decode; block diffusion hybrids) and compare latency/quality to pure AR and pure diffusion approaches.
- Diversity and calibration under SDE/ODE switching
- Study adaptive SDE↔ODE switching policies (per-sample) for balancing diversity and quality; define reliable early-stopping/confidence criteria for denoising.
- Multimodal extensions
- Evaluate CCDD where one modality is visual or acoustic (leveraging MM-DiT) to confirm benefits of coevolving continuous–discrete paths in true multimodal generation.
- Privacy and knowledge leakage
- Audit whether targeting pretrained embeddings leaks proprietary knowledge or training data; explore privacy-preserving training or differential privacy in the representation channel.
- Failure modes and diagnostics
- Identify and mitigate cases where one modality is ignored (e.g., discrete-only or continuous-only shortcutting); consider mutual-information regularizers or co-training signals enforcing cross-modal usage.
- End-to-end learning of the latent encoder
- Explore jointly training or fine-tuning the encoder with CCDD while preventing collapse; paper whether learned encoders outperform fixed external encoders and how to stabilize joint training.
- Evaluation breadth and interpretability
- Move beyond perplexity/NLL with human or automatic assessments of coherence, factuality, instruction adherence, and chain-of-thought validity; develop tools to visualize/interpret continuous latent trajectories.
- Reproducibility and standardization
- Release full hyperparameters (schedules, weights), code, and seeds; standardize evaluation (tokenizer-agnostic metrics, matched compute) to enable fair comparison across AR, discrete DLMs, and CCDD.
Practical Applications
Immediate Applications
Below are concrete, deployable use cases that leverage CCDD’s joint continuous–discrete diffusion, representation-guided sampling, and any-order generation. Each item lists likely sectors, potential tools/workflows, and feasibility assumptions.
- Lower-perplexity pretraining/fine-tuning for diffusion LMs
- Sectors: AI/ML platforms, academia
- Tools/workflows: Replace discrete-only DLMs with CCDD (MDiT/MMDiT/MoEDiT variants) to reduce perplexity on text corpora; plug in off-the-shelf encoders (e.g., Qwen3-Embedding, RoBERTa) to provide contextualized latent targets and implicit knowledge distillation.
- Assumptions/dependencies: Availability and licensing of high-quality embedding models; training compute for joint objectives; downstream gains beyond perplexity validated per task.
- Inference-time quality–efficiency tuning via ODE/SDE and representation CFG
- Sectors: Software, content platforms, cloud inference
- Tools/workflows: Serve one model with adjustable NFEs (few-step ODE for low latency; SDE for quality); steer outputs with “representation classifier-free guidance” (guidance weight w).
- Assumptions/dependencies: Sampler engineering for latency; guidance calibration; stability under different noise schedules.
- Editable, any-order text generation (fill-in-the-middle and local rewriting)
- Sectors: Productivity (docs, email), publishing, education
- Tools/workflows: Editor plugins that mask spans and invoke CCDD denoising to fill/repair text; parallel decoding for multi-span edits; self-correction loops without re-prompting.
- Assumptions/dependencies: Real-time budgets met with ODE sampling; UI integration; content safety guardrails.
- Retrieval-augmented generation alignment via representation conditioning
- Sectors: Enterprise search, legal, knowledge management
- Tools/workflows: Encode retrieved passages; use their contextual embeddings as latent guidance (representation CFG) to anchor generation to sources; combine with masked diffusion for “grounded rewriting.”
- Assumptions/dependencies: Embedding alignment between retriever and CCDD latent space; calibration to prevent over/under-conditioning.
- Code generation and repair with masked diffusion
- Sectors: Software engineering, DevOps
- Tools/workflows: IDE extensions for parallel candidate generation, local patching, lint-driven repairs; use any-order decoding to fix non-local bugs.
- Assumptions/dependencies: Training on code corpora/tokenizers; evaluation on compiler/test-suite outcomes; security scanning for generated code.
- Latent planning for structured reasoning tasks
- Sectors: Operations research (scheduling), gaming/puzzles
- Tools/workflows: Use continuous latent rollouts for planning/search (e.g., Sudoku, constraint puzzles); combine with discrete updates for exact decoding.
- Assumptions/dependencies: Task-specific fine-tuning; robustness to combinatorial constraints.
- Knowledge distillation and representation regularization
- Sectors: On-device NLP, model compression
- Tools/workflows: Train smaller CCDD models to reconstruct contextual embeddings from large encoders/LLMs (implicit distillation), improving convergence on limited compute.
- Assumptions/dependencies: Access to teacher embeddings; licensing; transfer holds across domains.
- Parallel decoding for latency-sensitive assistants
- Sectors: Customer support, real-time chat, call centers
- Tools/workflows: Generate partial responses in parallel; select via latent-space scoring; any-order edits to refine first-token latency vs final quality.
- Assumptions/dependencies: Serving infra for batched parallel denoising; guardrails to manage inconsistency across partial drafts.
- Evaluation and methodology research
- Sectors: Academia, standards bodies
- Tools/workflows: Benchmarks/studies isolating expressivity vs trainability; ablations on noise schedules, latent layer choice, and factorized kernels.
- Assumptions/dependencies: Public datasets with reasoning/structured targets; reproducible training pipelines.
Long-Term Applications
These use cases are promising but require further scaling, validation, or ecosystem development.
- Agentic systems with latent planning and tool use
- Sectors: Software agents, enterprise automation, robotics
- Tools/products: Agent frameworks where CCDD’s continuous latents perform plan/search over tools/APIs, with discrete steps for verifiable actions; backtracking/self-correction without external re-prompting.
- Assumptions/dependencies: Reliable interfaces to tools; safety constraints; evaluation of latent plans; compute budgets for longer SDE rollouts.
- Multimodal joint diffusion (text + vision/audio/code-structure)
- Sectors: Creative tools, assistive tech, autonomous systems
- Tools/products: Extend MMDiT/MoEDiT to jointly model text with images or ASTs/graphs, enabling cross-modal editing and grounded generation.
- Assumptions/dependencies: Large, aligned multimodal datasets; architecture/search for cross-modal factorization; compute for joint training.
- Safety and controllability via representation-level steering
- Sectors: Policy/regulation, enterprise compliance
- Tools/products: Policy knobs that steer latent concepts (e.g., toxicity reduction, style constraints) using representation CFG and asynchronous noise schedules; latent audit trails.
- Assumptions/dependencies: Validated mappings between latent directions and safety attributes; audit standards; calibration against distribution shift.
- Healthcare documentation and decision support with latent reasoning
- Sectors: Healthcare, life sciences
- Tools/products: Clinical note drafting with any-order edits; latent planning to structure differentials/workups before discrete summarization; controllable updates from EHR embeddings.
- Assumptions/dependencies: Regulatory approval; domain-specific training and rigorous clinical validation; privacy-preserving embedding pipelines.
- Finance/compliance drafting with parallel candidates and controllable interpolation
- Sectors: Finance, legal, risk
- Tools/products: Generate diverse, reviewable drafts in parallel; interpolate in latent space to meet risk/compliance constraints; self-correction passes before human sign-off.
- Assumptions/dependencies: Human-in-the-loop workflows; provenance tracking; robust steering that withstands adversarial prompts.
- Personalized education with iterative refinement
- Sectors: EdTech
- Tools/products: Tutors that plan lessons/solutions in latent space, then produce stepwise explanations; local remediation by masking/denoising challenging steps.
- Assumptions/dependencies: Pedagogically aligned datasets; evaluation for learning gains; guardrails for correctness.
- On-device efficient LMs with non-AR decoding and MoE routing
- Sectors: Mobile, embedded, edge AI
- Tools/products: CCDD with MoE (MoEDiT) to reduce compute while preserving parallel decoding; adaptive ODE sampling for low-power scenarios.
- Assumptions/dependencies: Kernel/runtime optimization for diffusion samplers; memory-efficient embedding extraction; quantization-friendly designs.
- Programming assistants that branch and reconcile plans
- Sectors: Software engineering platforms
- Tools/products: Speculative parallel branches in latent space (designs/tests/impl), reconciliation via denoising updates; structured code+AST joint diffusion.
- Assumptions/dependencies: High-quality AST corpora; robust merge strategies; cost-effective inference.
- Data-centric ML: controlled synthetic data generation
- Sectors: ML ops, privacy tech
- Tools/products: Use latent factors to generate datasets with targeted properties (class balance, style, linguistic phenomena); edit data via masked denoising.
- Assumptions/dependencies: Controls that translate to dataset-level properties; de-biasing; copyright/privacy compliance.
- Benchmarks and standards for latent reasoning and diffusion LMs
- Sectors: Policy, consortia, academia
- Tools/products: Standardized tasks/metrics for any-order editing, self-correction efficacy, latent-plan fidelity, and safety under representation steering.
- Assumptions/dependencies: Community consensus; open evaluation suites; reproducible baselines.
Notes on feasibility across applications:
- Performance depends on the quality/compatibility of contextual embeddings (layer choice, domain match); misalignment can hurt decoding fidelity.
- Joint modeling increases compute; practical deployments need optimized samplers, batching, and possibly distillation.
- Safety, attribution, and compliance require additional layers (filtering, retrieval grounding, human review).
- Gains shown on LM1B/OWT must be revalidated on larger, domain-specific corpora to ensure transferability.
Glossary
- Absorbing noise: A discrete diffusion corruption where tokens jump to a special mask state that absorbs them. "Masked (absorbing) noise, where we Augment with a mask state ."
- Absolutely continuous marginals: Probability distributions with densities (non-atomic) arising in continuous diffusion processes. "the Fokker-Planck equation in CDM would yield absolutely continuous marginals (Lemma~\ref{lem:ac_marginals})."
- Any-order generation: Non-autoregressive generation allowing tokens to be produced in arbitrary order. "The non-autoregressive nature of DLMs enables any-order generation, self-correction, and parallel decoding capabilities"
- Autoregressive (AR): A left-to-right generation paradigm where each token is conditioned on previous outputs. "autoregressive (AR) LLMs"
- Bayesian posterior: The posterior distribution computed via Bayes’ rule, used to form reverse kernels in discrete diffusion. "A Bayesian form of posterior is"
- Categorical distribution (Cat): A discrete probability distribution over a finite set of categories. "q_t(x_t|x_0)=\text{Cat}(\eta_t x_0+(1-\eta_t)\pi_t)"
- Chain-of-Thought (CoT): Explicit step-by-step reasoning traces generated during inference. "with logarithmic Chain-of-Thought (CoT) steps"
- Classifier-free guidance (CFG): A sampling technique combining conditional and unconditional predictions to steer outputs. "Classifier-free guidance (CFG)"
- Coevolutionary Continuous Discrete Diffusion (CCDD): The proposed joint diffusion framework over continuous representations and discrete tokens. "We therefore propose Coevolutionary Continuous Discrete Diffusion (CCDD), which defines a joint multimodal diffusion process"
- Consistency-based decoding: A method that enforces consistency across steps or models during decoding to improve sample quality. "including representation classifier-free guidance (CFG) and consistency-based decoding."
- Continuous diffusion models (CDMs): Diffusion models operating on continuous variables via SDEs or probability flow ODEs. "continuous diffusion models (CDMs) based on SDE or PF--ODE"
- Continuous-time Markov chain (CTMC): A stochastic process with continuous time transitions, used to corrupt discrete tokens. "based on the continuous-time Markov chain (CTMC)"
- DDIM (Denoising Diffusion Implicit Models): A deterministic sampler for diffusion models derived from the probability flow ODE. "as in DDPM~\citep{DDPM} and DDIM~\citep{DDIM}"
- DDPM (Denoising Diffusion Probabilistic Models): A classic stochastic diffusion framework with reverse-time denoising steps. "as in DDPM~\citep{DDPM} and DDIM~\citep{DDIM}"
- Denoising network: The neural network that predicts clean signals (or scores) from noisy inputs and time. "the denoising network predicts the clean data distribution"
- Diffusion LLMs (DLMs): LLMs that generate text via diffusion rather than autoregressive decoding. "diffusion LLMs (DLMs)"
- Diffusion Transformer (DiT): A transformer architecture adapted for diffusion modeling. "Inspired by DiT~\citep{dit}, MM-DiT~\citep{sd3}, and MoE~\citep{moe}"
- Discrete diffusion models (DDMs): Diffusion models defined on discrete token spaces via CTMCs. "discrete diffusion models (DDMs) based on the continuous-time Markov chain (CTMC)"
- Drift: The deterministic component of an SDE that guides the mean dynamics of the process. "with drift , scalar (or matrix) diffusion , and Wiener process ."
- ELBO (Evidence Lower Bound): A variational bound used to train diffusion models and relate to likelihood. "Based on the established ELBOs for continuous and discrete diffusion"
- Explicit Euler method: A basic numerical ODE integrator used to simulate looped transformer rollouts via PF–ODE. "explicit Euler method with step size $1/T$"
- Fokker–Planck PDE: The partial differential equation governing the time evolution of probability densities under SDEs. "The marginals satisfy the Fokker--Planck PDE"
- Function evaluations (NFEs): The count of model forward calls during sampling; fewer NFEs yield faster generation. "flexible number of function evaluations (NFEs)"
- Generator (CTMC): The rate matrix specifying transition intensities in a continuous-time Markov chain. "generator "
- Graph connectivity: A decision problem about whether nodes in a graph are connected, tied to multistep reasoning capacity. "graph connectivity that captures multistep reasoning ability"
- Knowledge distillation: Transferring knowledge from pretrained representations into the diffusion model during training. "can also be viewed as a sort of knowledge distillation."
- Latent reasoning: Performing reasoning in continuous latent spaces without decoding to discrete tokens at each step. "advantages of latent reasoning with looped transformers or continuous chain-of-thoughts"
- Looped transformer (LT): A transformer whose blocks are repeatedly applied (looped) to improve expressivity. "looped transformers (LT)"
- Mask state [MASK]: A special absorbing token used in masked diffusion corruption processes. "Augment with a mask state "
- MM-DiT: A multimodal variant of DiT used for joint denoising across modalities. "MM-DiT~\citep{sd3}"
- Modality-specific heads: Separate output layers for each modality (continuous and discrete) in a joint model. "outputs modality-specific heads"
- MoE (Mixture of Experts): An architecture with multiple expert subnetworks to improve parameter and compute efficiency. "MoE~\citep{moe}"
- Non-autoregressive: A generation paradigm that does not proceed strictly left-to-right, enabling parallel decoding. "The non-autoregressive nature of DLMs"
- Normalizing constant: A factor in time-ordered exponentials ensuring proper normalization of CTMC transitions. "( the normalizing constant)"
- Out-of-distribution (OOD): Inputs or rollouts differing from training conditions, often causing performance issues. "out-of-distribution (OOD) issues."
- PF–ODE (Probability Flow ODE): The deterministic ODE corresponding to the diffusion process’s probability flow. "based on SDE or PF--ODE"
- Probability simplex: The set of valid probability vectors with nonnegative entries summing to one. "simplex "
- Pushforward: The distribution induced by mapping a random variable through a function (e.g., an encoder). "(the pushforward by the fixed encoder )"
- Rao-Blackwellized likelihood bounds: Tighter bounds obtained by conditioning, used to weight training losses in discrete diffusion. "with weights $\lambda_{\mathrm{disc}(t, x_t,x_0)$ derived from Rao-Blackwellized likelihood bounds"
- Representation regularization: Regularizing training by reconstructing high-quality pretrained representations. "serve as representation regularization that accelerates the convergence of training"
- Reverse SDE: The reverse-time stochastic differential equation used for sampling in diffusion models. "The reverse process is based on the reverse SDE"
- Rotary embeddings: A positional encoding technique for transformers that rotates feature dimensions. "which augments DiT~\citep{dit} with rotary embeddings~\citep{roformer}"
- SDE (Stochastic Differential Equation): An equation describing continuous-time dynamics driven by randomness. "based on SDE or PF--ODE"
- Self-correction capabilities: The ability of models to iteratively refine outputs during generation. "enables any-order generation, self-correction, and parallel decoding capabilities"
- Semigroups: Algebraic structures describing composable time-evolution operators in stochastic processes. "the factored forward processes admit semigroups~(\Cref{lem:trotter})"
- Signal-noise ratios (SNR): Ratios controlling the relative strength of signal versus noise in corruption schedules. "approximately synchronous signal-noise ratios in two modalities"
- Timestep embeddings: Time-conditioning features that can enhance the expressiveness of diffusion or looped models. "timestep embeddings improve expressiveness"
- Universal transformers: Transformers with shared parameters across layers enabling variable-depth computation. "looped transformers or universal transformers~\citep{dehghani2018universal}"
- Variance preserving (VP) schedule: A noise schedule where variance is preserved across time in the forward SDE. "A standard instance is the variance preserving (VP) schedule"
- Wiener process: Standard Brownian motion used as the driving noise in SDEs. "Wiener process "
Collections
Sign up for free to add this paper to one or more collections.