Tracing the Representation Geometry of Language Models from Pretraining to Post-training (2509.23024v1)

Abstract: Standard training metrics like loss fail to explain the emergence of complex capabilities in LLMs. We take a spectral approach to investigate the geometry of learned representations across pretraining and post-training, measuring effective rank (RankMe) and eigenspectrum decay ($\alpha$-ReQ). With OLMo (1B-7B) and Pythia (160M-12B) models, we uncover a consistent non-monotonic sequence of three geometric phases during autoregressive pretraining. The initial "warmup" phase exhibits rapid representational collapse. This is followed by an "entropy-seeking" phase, where the manifold's dimensionality expands substantially, coinciding with peak n-gram memorization. Subsequently, a "compression-seeking" phase imposes anisotropic consolidation, selectively preserving variance along dominant eigendirections while contracting others, a transition marked with significant improvement in downstream task performance. We show these phases can emerge from a fundamental interplay of cross-entropy optimization under skewed token frequencies and representational bottlenecks ($d \ll |V|$). Post-training further transforms geometry: SFT and DPO drive "entropy-seeking" dynamics to integrate specific instructional or preferential data, improving in-distribution performance while degrading out-of-distribution robustness. Conversely, RLVR induces "compression-seeking", enhancing reward alignment but reducing generation diversity.

• The paper identifies three universal geometric phases—Gray, Maroon, and BlueViolet—that correlate with evolving LLM capabilities.
• It leverages spectral metrics, including RankMe and eigenspectrum decay, to quantify non-monotonic changes in representation geometry during pretraining and post-training.
• The study shows that post-training techniques mirror pretraining dynamics, influencing model memorization, generalization, and alignment.

Spectral Phases in the Geometric Evolution of LLM Representations

Introduction

This paper presents a comprehensive spectral analysis of the geometric evolution of representations in LLMs throughout both pretraining and post-training stages. By leveraging spectral metrics—effective rank ($RankMe$) and eigenspectrum decay ($\alpha$)—the authors reveal a consistent, non-monotonic sequence of three universal geometric phases in LLM training: Gray, Maroon, and BlueViolet. These phases are shown to be robust across model families (OLMo, Pythia, T\"ulu), scales (160M–12B parameters), and layers, and are tightly linked to the emergence of distinct model capabilities, including memorization and generalization. The work further demonstrates that post-training strategies (SFT, DPO, RLVR) induce mirrored geometric transformations, with practical implications for model alignment and exploration.

Figure 1: Spectral framework reveals three universal phases in LLM training, characterized by distinct changes in representation geometry.

Spectral Metrics and Geometric Analysis

The analysis centers on the covariance matrix of last-token representations in autoregressive LLMs. Two complementary spectral metrics are employed:

• Effective Rank ($RankMe$): Derived from the Von Neumann entropy of the covariance matrix, quantifies the utilized dimensionality of the representation manifold.
• Eigenspectrum Decay ($\alpha$): Measures the concentration of variance along principal axes, with slower decay indicating higher-dimensional, more isotropic representations.

These metrics provide a quantitative lens for tracking the expressive capacity and compression of LLM representations, moving beyond traditional loss curves which fail to capture qualitative shifts in model behavior.

Three-Phase Dynamics in Pretraining

Empirical analysis across OLMo and Pythia models reveals a non-monotonic evolution of representation geometry, consistently manifesting as three distinct phases:

1. Gray Phase: Rapid collapse of representations onto dominant data manifold directions, coinciding with learning rate ramp-up. Outputs are repetitive and non-contextual.
2. Maroon Phase: Manifold expansion in many directions, marked by increased $RankMe$ and decreased $\alpha$. This phase aligns with peak n-gram memorization, as measured by Spearman correlation with $\infty$-gram models.
3. BlueViolet Phase: Anisotropic consolidation, with selective preservation of variance along dominant eigendirections and contraction of others. $RankMe$ decreases, $\alpha$ increases, and long-context generalization capabilities emerge.

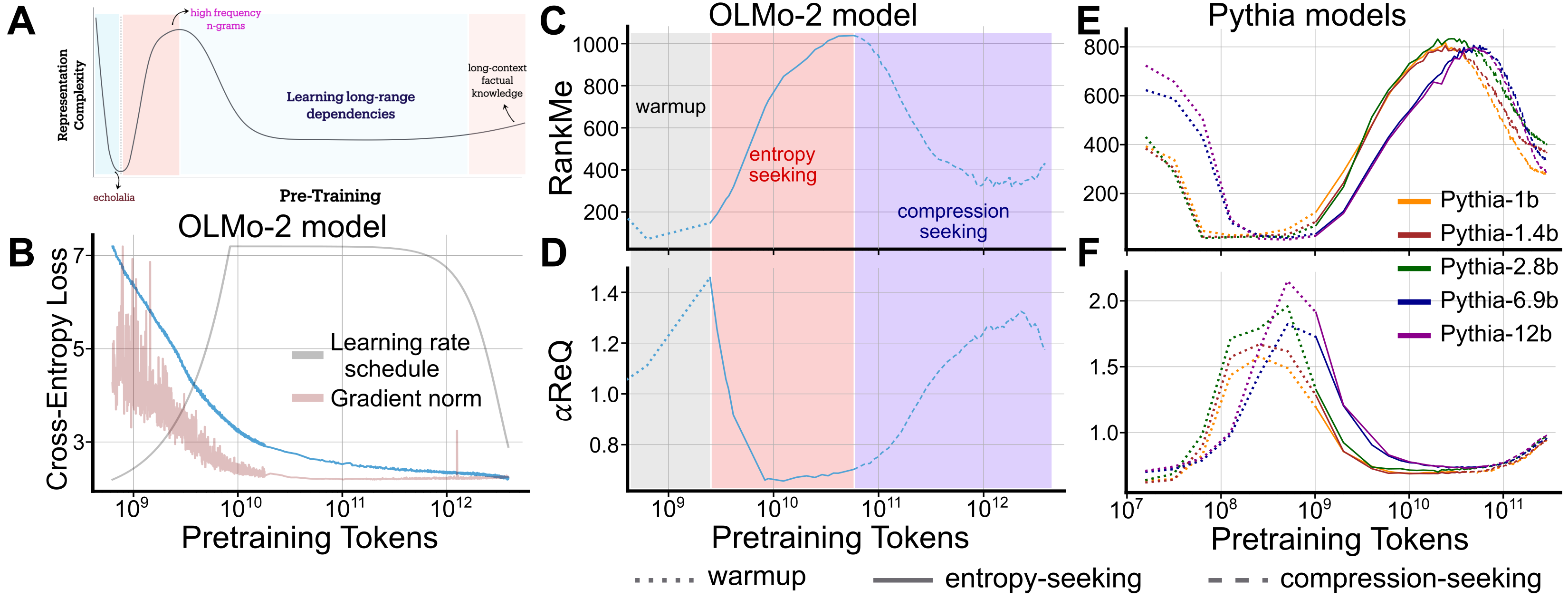
   Figure 2: Loss decreases monotonically, but representation geometry exhibits non-monotonic transitions through Gray, Maroon, and BlueViolet phases across model families and scales.

   

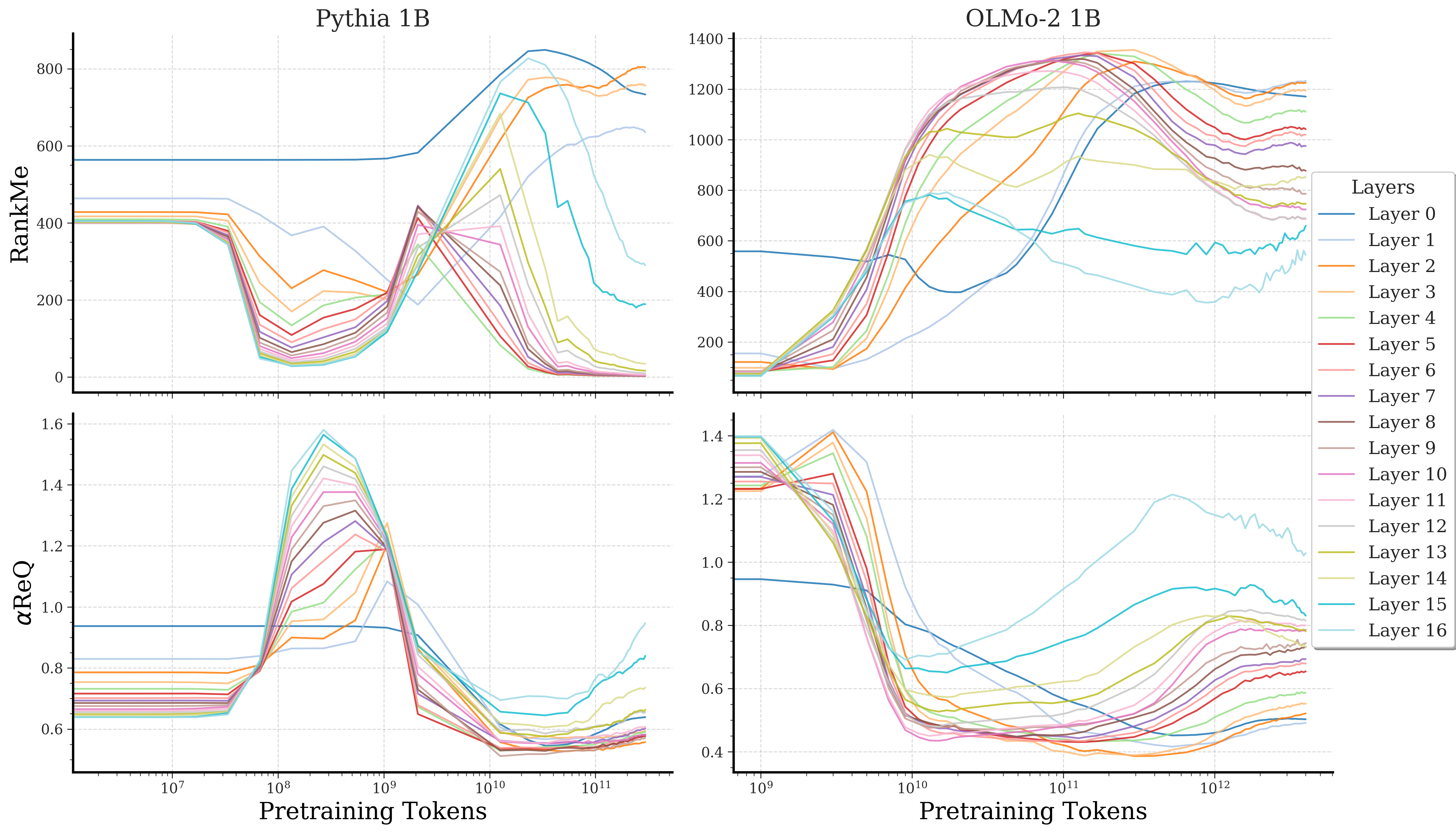
   Figure 3: Layerwise evolution mirrors the three-phase pattern, confirming global geometric dynamics across network depth.

Linking Geometry to Model Capabilities

The Maroon phase is associated with short-context memorization, as evidenced by increased alignment with n-gram statistics. In contrast, the BlueViolet phase correlates with the emergence of long-context generalization, as demonstrated by improved performance on factual QA tasks (TriviaQA) and multiple-choice tasks (SciQ).

Figure 4: Distinct learning phases are linked to different LLM capabilities; memorization peaks in Maroon, while generalization and task accuracy surge in BlueViolet.

Ablation experiments show that retaining only top eigen-directions severely degrades task accuracy, indicating that full-spectrum information is essential for robust language understanding.

Mechanistic Insights: Optimization and Bottlenecks

Analytically tractable models reveal that the observed multiphase dynamics arise from the interplay of cross-entropy optimization, skewed token frequencies, and representational bottlenecks ($d \ll |\mathcal{V}|$). Gradient descent exhibits primacy and selection biases, leading to initial collapse, expansion, and subsequent anisotropic consolidation of representations.

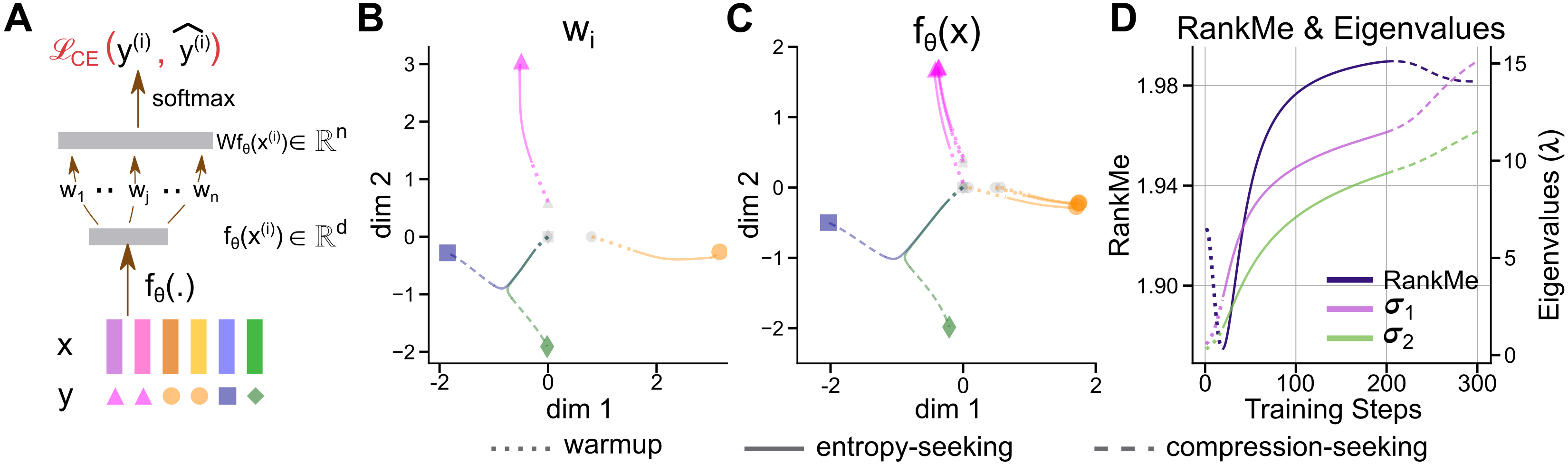
Figure 5: Learning dynamics of cross-entropy loss replicate multiphase geometric evolution, contingent on skewed class distribution and information bottleneck.

Negative controls (uniform labels, no bottleneck, MSE loss) eliminate the BlueViolet phase, isolating necessary conditions for the observed dynamics.

Post-Training: Alignment and Exploration Trade-offs

Post-training strategies induce distinct geometric transformations:

• Supervised Fine-Tuning (SFT) and Direct Preference Optimization (DPO): Both drive Maroon-like expansion, increasing $RankMe$ and enhancing in-distribution fit but increasing sensitivity to dataset idiosyncrasies and reducing out-of-distribution robustness.
• Reinforcement Learning from Verifiable Rewards (RLVR): Induces BlueViolet-like contraction, consolidating reward-aligned behaviors and narrowing generative diversity, as evidenced by reduced pass@$k$ performance at high $k$.

  Figure 6: Post-training induces distinct geometric transformations in model representations, with SFT/DPO expanding and RLVR contracting the representation manifold.

These mirrored spectral transformations have practical implications for model selection, checkpointing, and the design of training pipelines tailored to desired downstream outcomes.

Implications and Future Directions

The identification of universal geometric phases provides a quantitative framework for understanding the emergence of memorization and generalization in LLMs. The necessity of full-spectrum information for downstream performance underscores the limitations of top-$k$ proxies and motivates the use of comprehensive spectral metrics. The geometric perspective offers mechanistic explanations for phenomena such as grokking and staged learning, and informs the design of post-training interventions for alignment and exploration.

Limitations include computational constraints (analysis up to 12B parameters), reliance on linearized theoretical models, and focus on English-LLMs. Future work should extend these findings to larger scales, multilingual settings, and more complex architectures, and establish causal links between geometric dynamics and emergent capabilities.

Conclusion

This work demonstrates that LLMs undergo non-monotonic, multiphasic changes in representation geometry during both pretraining and post-training, often masked by monotonically decreasing loss. Spectral metrics ($RankMe$, $\alpha$) delineate three universal phases—Gray, Maroon, BlueViolet—each linked to distinct model capabilities. Post-training strategies induce mirrored geometric transformations, with practical trade-offs for alignment and exploration. These insights provide a principled foundation for guiding future advancements in LLM development, checkpoint selection, and training strategy design.