- The paper demonstrates that LLMs encode a latent correctness signal using linear probes on activations after the question prompt.
- Methodology leveraging layer-wise analysis distinguishes between correct, incorrect, and abstaining responses across diverse datasets.
- Empirical results reveal efficient prediction of answer accuracy, though the signal fails to generalize to mathematical reasoning tasks.
Predicting LLM Answer Accuracy from Question-Only Linear Probes
Introduction
This paper investigates whether LLMs encode, in their internal activations, a latent signal that predicts the correctness of their forthcoming answers—before any tokens are generated. The authors propose a methodology that leverages linear probes on the residual stream activations at the end of the question prompt to extract a direction in activation space that discriminates between questions the model will answer correctly and those it will not. This approach is evaluated across multiple open-source LLMs (7B–70B parameters) and a diverse set of knowledge and reasoning datasets. The results demonstrate that this "in-advance correctness direction" is robust, generalizes across domains, and correlates with abstention behavior (e.g., "I don't know" responses), but fails to generalize to mathematical reasoning tasks.
Methodology
The core method involves extracting the residual stream activations from each layer of an LLM after processing the final token of a question prompt, but before answer generation. The process is as follows:
- Activation Extraction: For each question, activations are collected at each layer after the last prompt token.
- Answer Generation and Labeling: The model generates an answer, which is evaluated for correctness.
- Direction Identification: For a given layer, the mean activation vectors for correctly and incorrectly answered questions are computed. The difference between these centroids defines the "correctness direction."
- Layer Selection: The layer with the highest discriminative power (as measured by AUROC) is selected.
- Probe Training and Evaluation: A linear probe is trained on the selected layer, and its performance is evaluated both in-distribution and out-of-distribution.
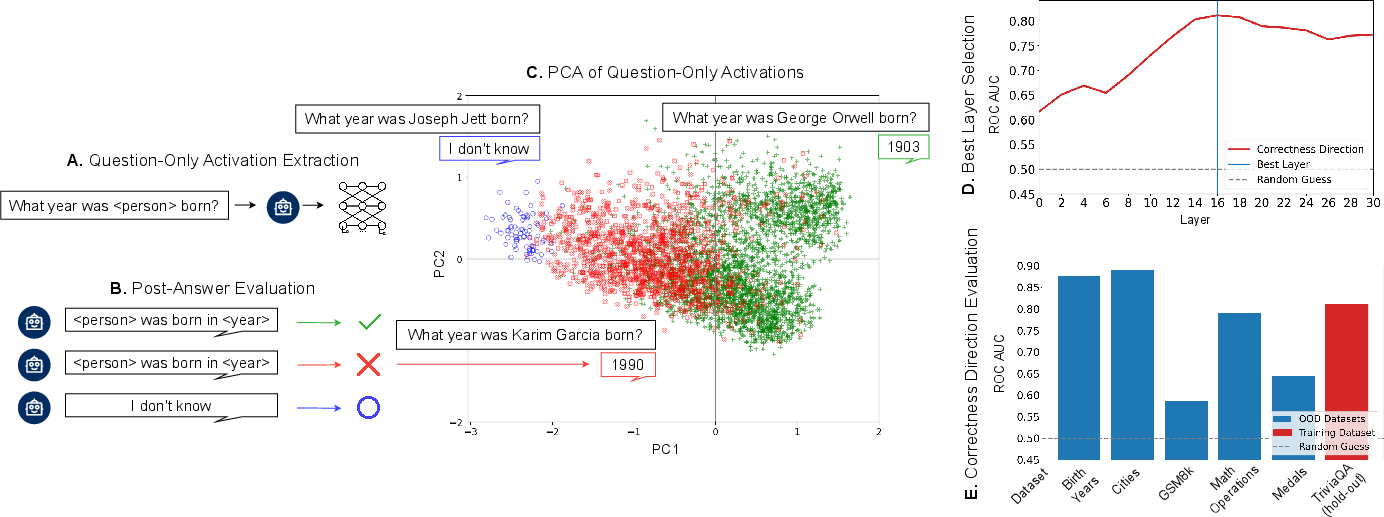
Figure 1: The methodology for extracting the in-advance correctness direction from LLM activations, including activation extraction, answer evaluation, direction identification, layer selection, and probe training.
The correctness score for a given activation h is computed as the projection onto the normalized correctness direction w:
score(h)=∥w∥(h−μ)⊤w
where μ is the mean of the centroids for correct and incorrect answers.
Empirical Results
Layerwise Emergence of Correctness Signal
The discriminative power of the correctness direction varies across layers. For all tested models, AUROC for predicting answer correctness from activations increases with depth, saturating in intermediate layers and sometimes declining in the final layers. This suggests that the model's internal assessment of its own competence emerges mid-computation.
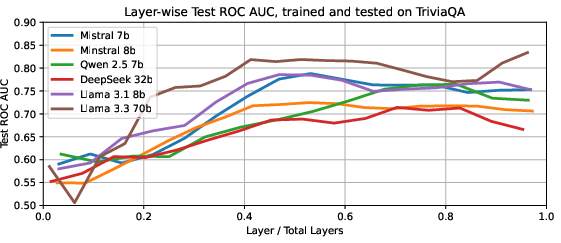
Figure 2: AUROC for predicting correctness from activations across layers, showing performance saturation in intermediate layers for both small and large models.
Generalization Across Datasets and Models
The probe trained on a general knowledge dataset (TriviaQA) generalizes well to other factual knowledge datasets (e.g., Cities, Notable People, Medals), outperforming both black-box assessors (trained on question embeddings) and verbalized confidence baselines. However, all methods—including the probe—fail to generalize to GSM8K, a mathematical reasoning dataset, indicating a limitation in the internal representation of correctness for tasks requiring multi-step reasoning.
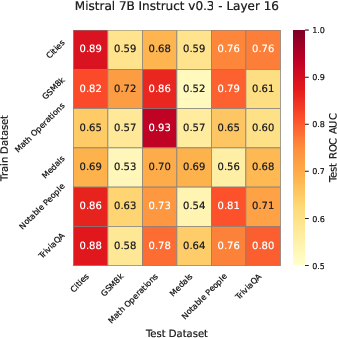
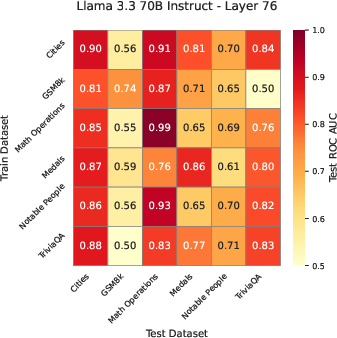
Figure 3: AUROC scores for the correctness direction trained on each dataset, evaluated across datasets and models, highlighting strong generalization for knowledge tasks but not for mathematical reasoning.
Data Efficiency and Model Scaling
The number of training samples required to learn a high-quality correctness direction is modest: as few as 160 samples suffice for reasonable performance, and 2560 samples are sufficient to saturate AUROC on most datasets. Larger models require fewer samples to reach peak performance, and the correctness signal is strongest in the largest model tested (Llama 3.3 70B).
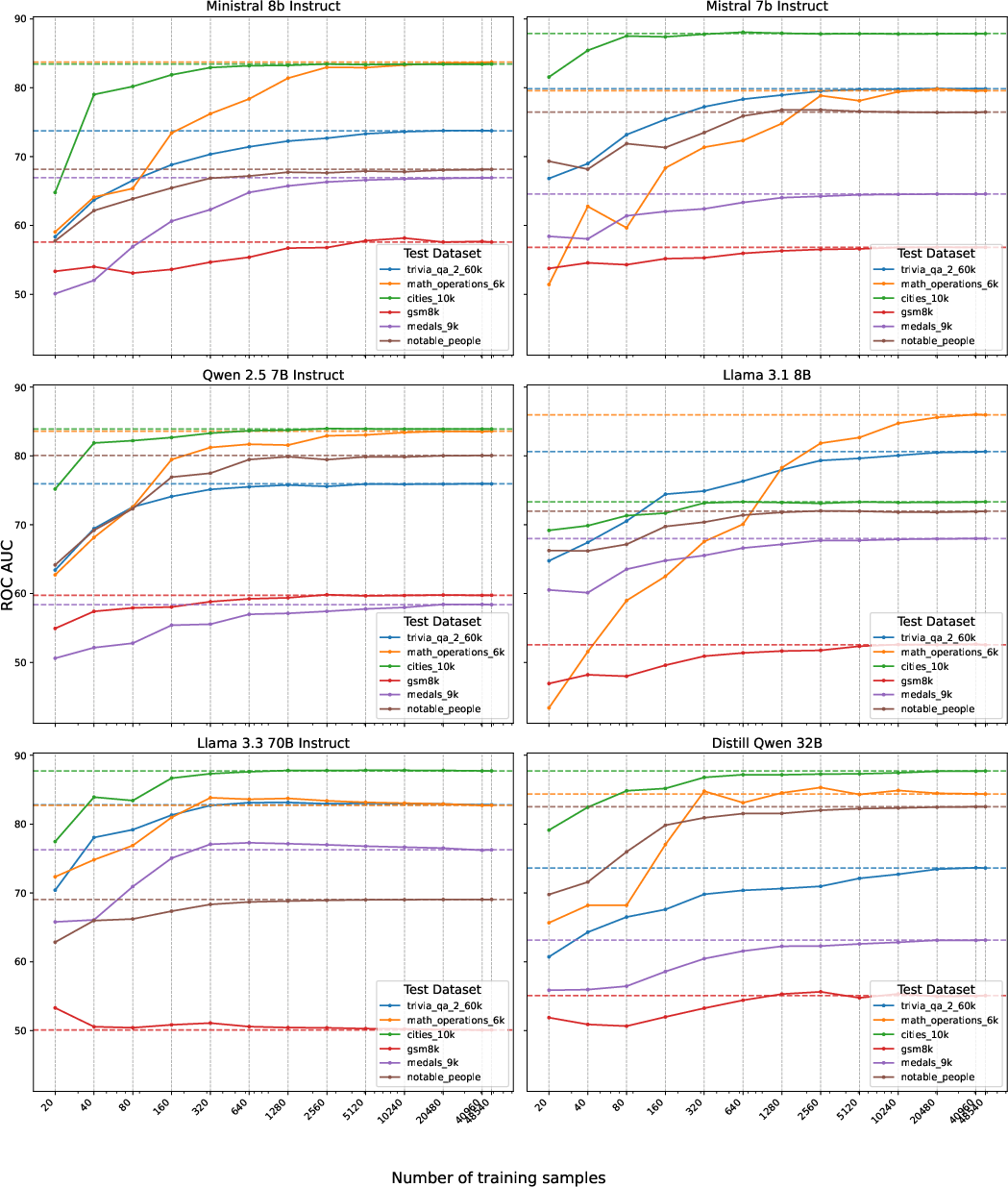
Figure 4: AUROC as a function of training set size for the correctness direction, showing rapid saturation and greater data efficiency in larger models.
Alignment with Abstention and Confidence
For models that spontaneously respond "I don't know," these responses are strongly correlated with low values along the correctness direction. This suggests that the same direction encodes both correctness and confidence, and that the model's internal state prior to answer generation is predictive of both answer accuracy and abstention behavior.
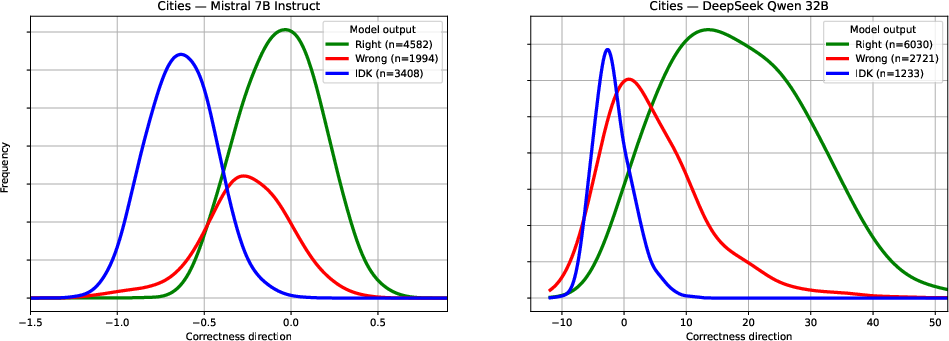
Figure 5: Distribution of activation projections on the correctness direction, grouped by answer type ("right", "wrong", "I don't know"), showing that abstentions cluster at the low-confidence extreme.
Analysis and Implications
Robustness and Limitations
- Robustness: The correctness direction is robust across model families and scales, and generalizes across factual knowledge domains. The direction learned on a diverse dataset (TriviaQA) is less susceptible to overfitting to dataset-specific artifacts than directions learned on narrow domains.
- Limitations: The approach fails to generalize to mathematical reasoning tasks (GSM8K), indicating that the internal representation of correctness for such tasks is either absent or not linearly accessible at the prompt stage. Additionally, the method assumes white-box access to model activations.
Comparison to Baselines
- Verbalized Confidence: Prompting the model to report its own confidence yields poor discriminative power, especially out-of-distribution.
- Black-box Assessors: Assessors trained on question embeddings overfit in-distribution and generalize poorly, whereas the linear probe on model internals is more robust to domain shift.
Mechanistic Interpretability
The existence of a linearly accessible correctness direction in LLM activations supports the hypothesis that models internally encode a notion of their own competence, accessible before answer generation. This finding complements prior work on truthfulness and hallucination detection via model internals, and aligns with results from sparse auto-encoder analyses.
Practical Applications
- Early Failure Detection: The correctness direction can be used to flag questions likely to be answered incorrectly before answer generation, enabling early stopping, fallback, or human-in-the-loop interventions.
- Low-Cost Uncertainty Quantification: The probe requires only a single forward pass and a linear projection, making it computationally efficient compared to sampling-based uncertainty estimation.
- Model Steering: The direction could potentially be used for activation steering to modulate model confidence or refusal behavior.
Future Directions
- Nonlinear Probes: Exploring higher-capacity probes may reveal additional structure in the internal representation of correctness, especially for complex reasoning tasks.
- Stochasticity and Ambiguity: Extending the method to account for answer stochasticity and ambiguous questions could improve robustness.
- Broader Model Coverage: Applying the approach to proprietary models, alternative architectures, and future frontier systems would test its generality.
- Layerwise and Temporal Analysis: Investigating the temporal evolution of the correctness signal during autoregressive generation may yield further insights.
Conclusion
This work demonstrates that LLMs encode a latent, linearly accessible signal in their internal activations that predicts answer correctness before any output is generated. This signal is robust across models and factual knowledge domains, aligns with abstention behavior, and is strongest in larger models. However, it does not generalize to mathematical reasoning tasks, highlighting a limitation in current LLM architectures. The findings have significant implications for mechanistic interpretability, AI safety, and the practical deployment of LLMs in high-stakes settings, providing a foundation for efficient, internal uncertainty quantification and early failure detection.





