The Illusion of Diminishing Returns: Measuring Long Horizon Execution in LLMs (2509.09677v1)

Abstract: Does continued scaling of LLMs yield diminishing returns? Real-world value often stems from the length of task an agent can complete. We start this work by observing the simple but counterintuitive fact that marginal gains in single-step accuracy can compound into exponential improvements in the length of a task a model can successfully complete. Then, we argue that failures of LLMs when simple tasks are made longer arise from mistakes in execution, rather than an inability to reason. We propose isolating execution capability, by explicitly providing the knowledge and plan needed to solve a long-horizon task. We find that larger models can correctly execute significantly more turns even when small models have 100\% single-turn accuracy. We observe that the per-step accuracy of models degrades as the number of steps increases. This is not just due to long-context limitations -- curiously, we observe a self-conditioning effect -- models become more likely to make mistakes when the context contains their errors from prior turns. Self-conditioning does not reduce by just scaling the model size. In contrast, recent thinking models do not self-condition, and can also execute much longer tasks in a single turn. We conclude by benchmarking frontier thinking models on the length of task they can execute in a single turn. Overall, by focusing on the ability to execute, we hope to reconcile debates on how LLMs can solve complex reasoning problems yet fail at simple tasks when made longer, and highlight the massive benefits of scaling model size and sequential test-time compute for long-horizon tasks.

• The paper demonstrates that marginal improvements in single-step accuracy can compound to enable exponential increases in the length of tasks LLMs can reliably execute.
• The authors introduce a synthetic 'retrieve-then-compose' task to isolate execution, showing that scaling model size significantly extends long-horizon performance.
• The study identifies a self-conditioning effect where prior errors compound, and reveals that sequential test-time compute (thinking) mitigates these execution failures.

Measuring Long-Horizon Execution in LLMs: Challenging the Illusion of Diminishing Returns

Introduction and Motivation

The paper "The Illusion of Diminishing Returns: Measuring Long Horizon Execution in LLMs" (2509.09677) addresses a central question in the development and deployment of LLMs: does continued scaling of LLMs yield diminishing returns, particularly in the context of executing long-horizon tasks? While scaling laws for LLMs indicate diminishing improvements in standard metrics such as test loss, the economic and practical value of LLMs is increasingly tied to their ability to reliably execute long, multi-step tasks. The authors argue that marginal improvements in single-step accuracy can compound to yield exponential gains in the length of tasks that a model can complete without error, and that failures on long tasks are often due to execution errors rather than deficiencies in reasoning or planning.

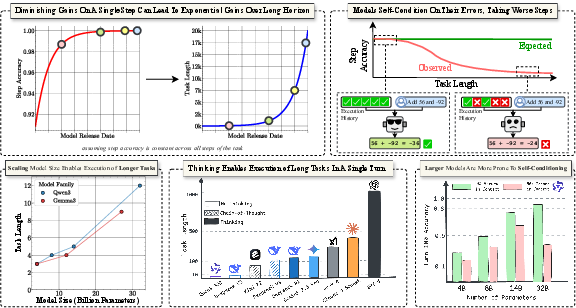
Figure 1: Summary of contributions, highlighting that diminishing returns in step accuracy can enable exponential gains in horizon length, and that both model scaling and test-time compute benefit long-horizon execution.

Theoretical Analysis: Compounding Effects of Step Accuracy

The authors provide a formal analysis of the relationship between single-step accuracy and the maximum task length (horizon length) that a model can execute with a given success probability. Under the assumption of constant per-step accuracy $p$ and no self-correction, the probability of completing a task of length $H$ is $p^H$. Solving for $H$ at a fixed success rate $s$ yields:

$H_s(p) = \frac{\ln(s)}{\ln(p)}$

This result demonstrates that as step accuracy approaches 1, even small improvements in $p$ can lead to super-exponential increases in $H_s$. In the high-accuracy regime, the sensitivity of horizon length to step accuracy is quadratic, i.e., $$\Delta H_{0.5} \approx \frac{\ln 2}{(1-p)^2}\,\Delta p$$. This compounding effect implies that the economic value of LLMs, when measured by the length of tasks they can reliably execute, may continue to grow rapidly even as traditional benchmarks suggest slowing progress.

Experimental Framework: Isolating Execution from Planning and Knowledge

To empirically paper long-horizon execution, the authors design a synthetic task that explicitly decouples execution from planning and knowledge. The task is structured as a sequence of "retrieve-then-compose" steps: at each turn, the model is provided with a plan (a set of keys) and a dictionary mapping keys to integer values. The model must retrieve the values and maintain a running sum, with the plan and knowledge provided in-context, thus removing the need for parametric knowledge or planning.

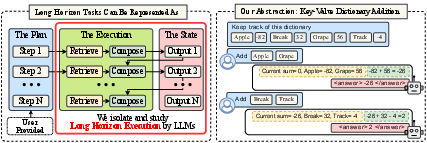
Figure 2: Framework overview—long-horizon tasks are modeled as retrieve-then-compose steps, with planning and knowledge ablated to isolate execution.

This setup allows precise control over two axes: the number of turns (task length) and the turn complexity (number of steps per turn). The simplicity of the task ensures that any degradation in performance is attributable to execution failures rather than reasoning or knowledge deficits.

Empirical Results: Scaling, Self-Conditioning, and the Role of Thinking

Scaling Model Size

Experiments with Qwen3 and Gemma3 model families across multiple sizes reveal that, even when all but the smallest models achieve 100% single-step accuracy, task accuracy degrades rapidly as the number of turns increases. Larger models sustain high accuracy over significantly more turns, indicating a non-diminishing benefit of scaling for long-horizon execution, even in the absence of increased task complexity or knowledge requirements.

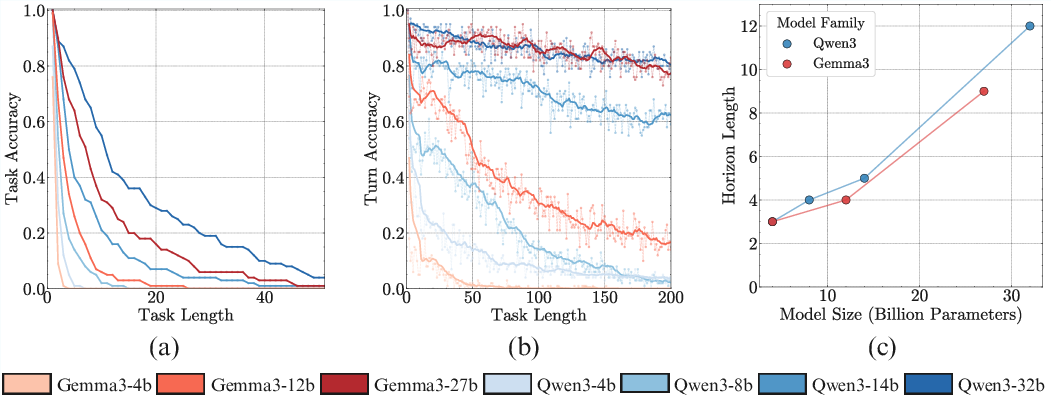
Figure 3: Scaling model size non-diminishingly improves the number of turns a model can execute; the performance gap between small and large models widens with task length.

Self-Conditioning Effect

A key empirical finding is the "self-conditioning" effect: as models observe their own prior mistakes in the context, the likelihood of future errors increases. This effect is distinct from long-context degradation and is not mitigated by scaling model size. Counterfactual experiments, where the error rate in the model's history is manipulated, show that turn accuracy at a fixed position (e.g., turn 100) degrades sharply as the fraction of prior errors increases.

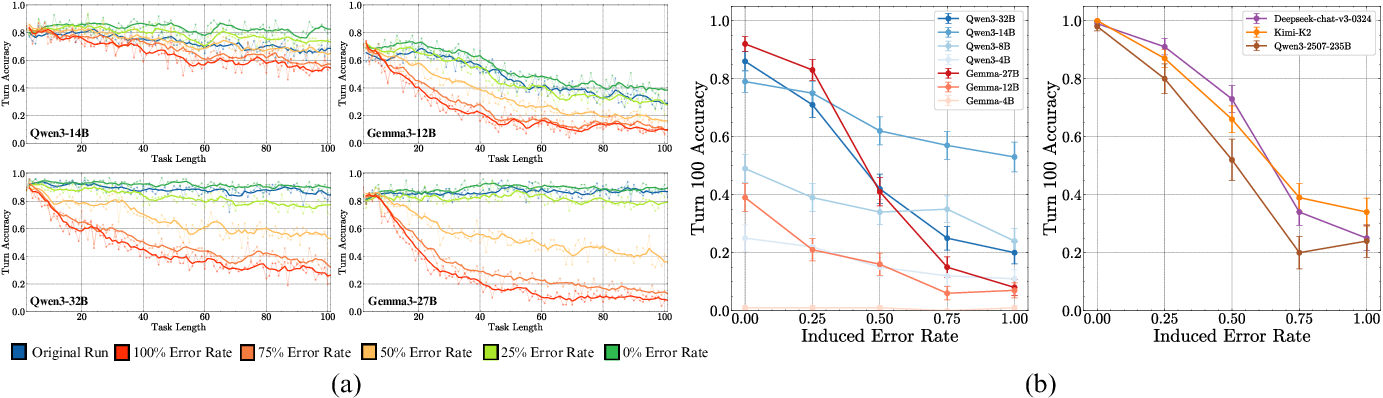
Figure 4: Models self-condition on previous mistakes, leading to compounding errors in subsequent turns; scaling model size does not eliminate this effect.

Sequential Test-Time Compute and "Thinking" Models

The introduction of sequential test-time compute—i.e., enabling models to generate explicit reasoning traces ("thinking")—substantially improves long-horizon execution. RL-trained "thinking" models do not exhibit self-conditioning: their accuracy remains stable regardless of the error rate in prior turns. Moreover, these models can execute significantly more steps in a single turn compared to non-thinking models.

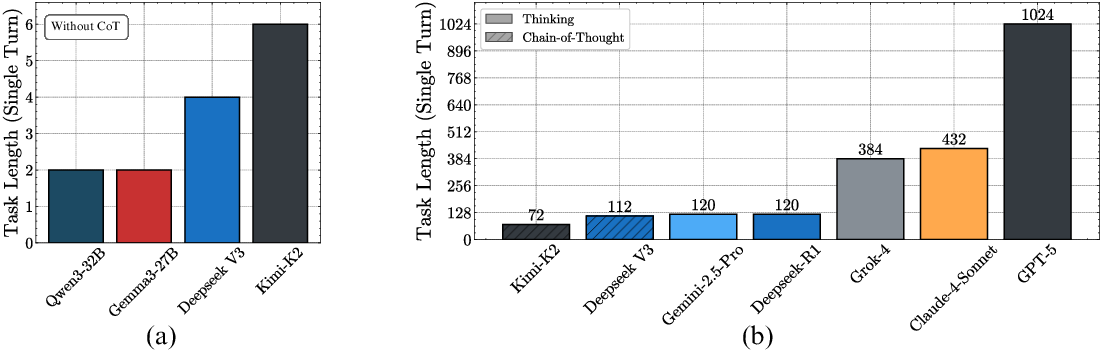
Figure 5: Benchmarking single-turn execution—without CoT, even the largest models fail at multi-step execution; thinking models, especially GPT-5, achieve orders-of-magnitude longer horizons.

Analysis of Failure Modes and Mitigation Strategies

The authors further analyze the sources of execution failure. Decomposition of the task into retrieval and addition reveals that models perform well on these operations in isolation, but struggle with state management over long horizons. Format-following errors are minimal and not the primary source of degradation.

Attempts to mitigate self-conditioning via self-verification prompting are only partially successful and incur significant context and compute costs. In contrast, context management strategies—such as limiting the context window to recent turns—can reduce self-conditioning in Markovian tasks, but are not generally applicable to tasks with long-range dependencies.

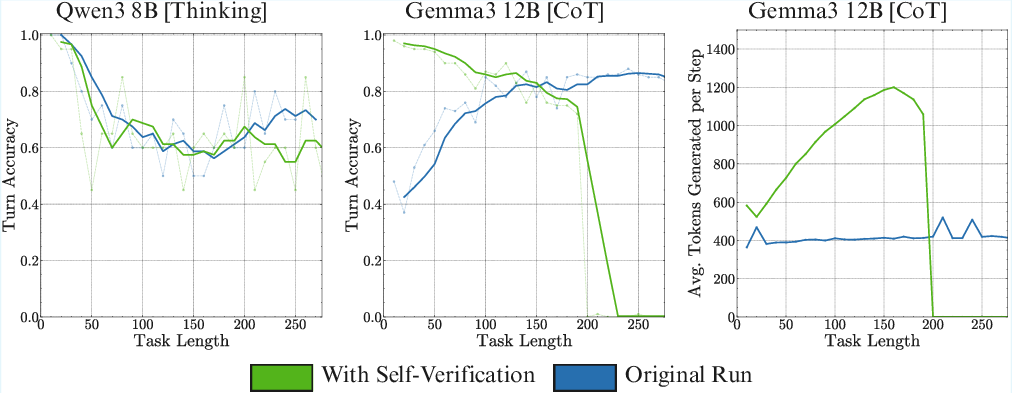
Figure 6: Self-verification prompting does not fully resolve self-conditioning and increases context consumption.

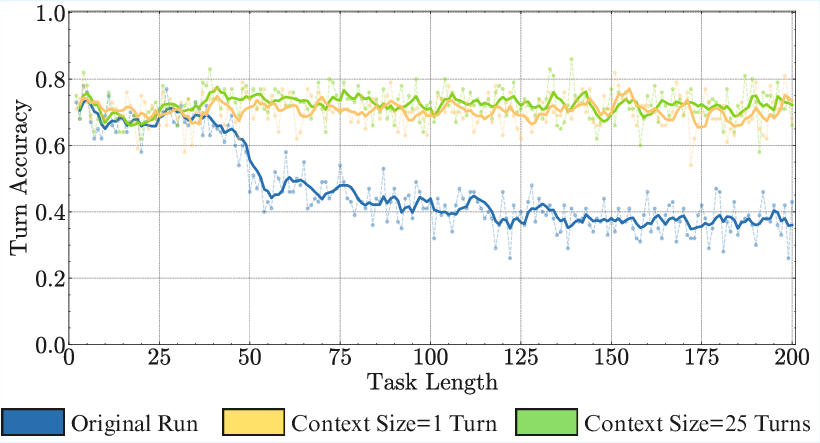
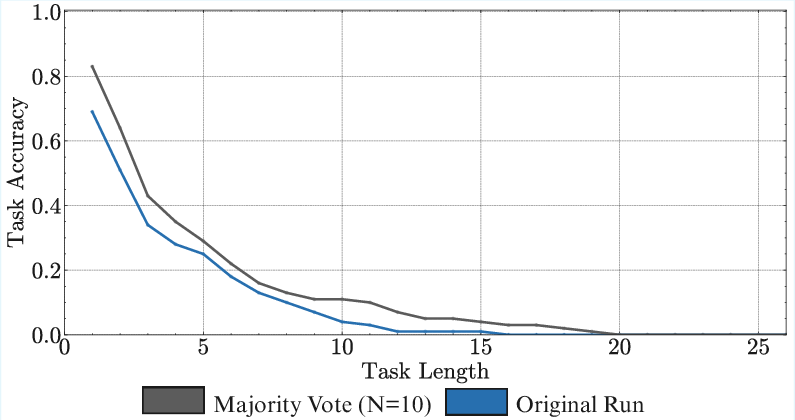
Figure 7: Context management (sliding window) reduces self-conditioning but is only viable for Markovian tasks.

Turn Complexity, Test-Time Compute, and Scaling Trends

The relationship between turn complexity and horizon length is nontrivial. For a fixed total number of steps, varying the number of steps per turn leads to different outcomes across model families, with no universal trend. Enabling sequential test-time compute (thinking) allows models to handle higher turn complexity, and scaling trends persist even in this regime.

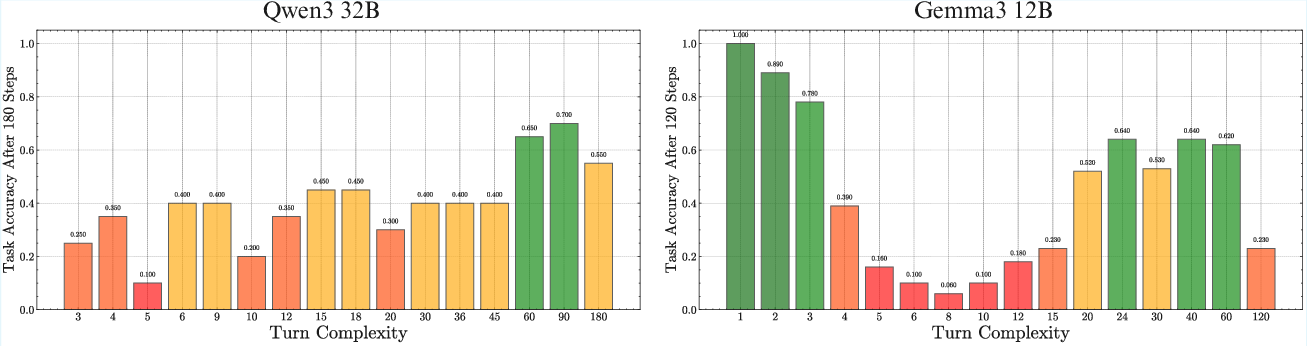
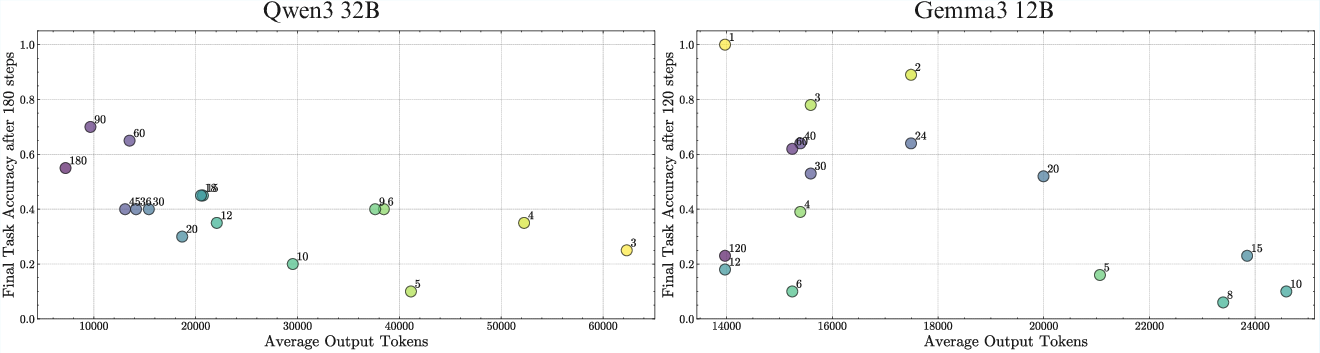
Figure 8: For the same total steps, different turn complexities yield different outcomes across model families.

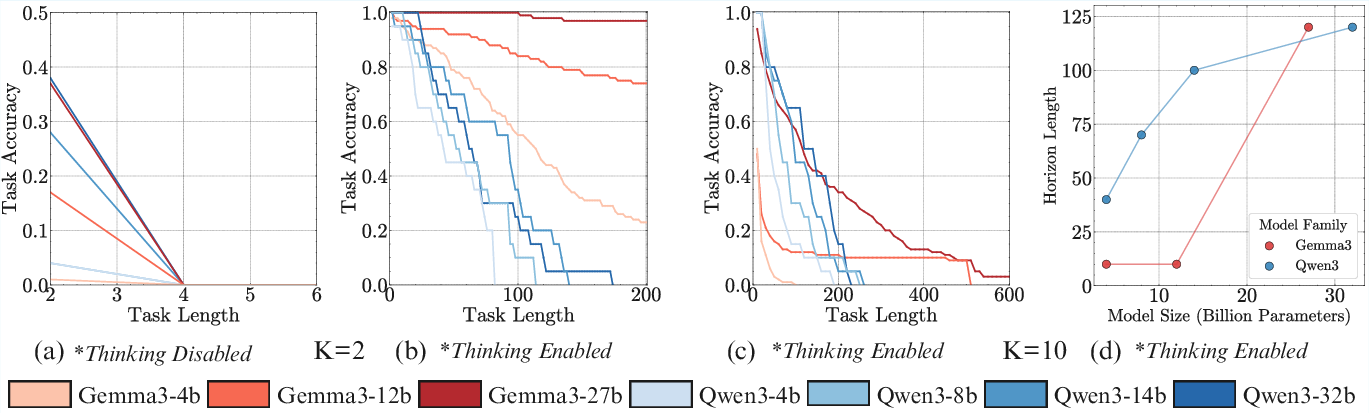
Figure 9: Scaling trends hold with sequential test-time compute; thinking enables models to handle higher turn complexity, and larger models achieve longer horizons.

Implications and Future Directions

The findings have several important implications:

• Economic Value of Scaling: The compounding effect of step accuracy on horizon length suggests that continued investment in scaling LLMs may be justified, even as traditional benchmarks show diminishing returns.
• Execution as a Bottleneck: Execution failures, rather than reasoning or planning, are a primary bottleneck for long-horizon tasks. This challenges the interpretation of long-horizon failures as evidence of reasoning limitations.
• Self-Conditioning as a Reliability Challenge: The self-conditioning effect introduces a new axis of unreliability in LLMs, distinct from long-context degradation, and is not addressed by simply scaling model size.
• Superiority of Sequential Test-Time Compute: Sequential reasoning (thinking) at test time is more effective than parallel strategies (e.g., majority voting) for long-horizon execution, especially in tasks requiring state management.
• Benchmarking and Evaluation: The proposed synthetic task provides a contamination-free, controlled benchmark for long-horizon execution, complementing real-world agentic benchmarks.

Theoretically, these results motivate the paper of empirical scaling laws for horizon length, and the development of architectures and training regimes that explicitly target execution reliability over long horizons. Practically, they highlight the need for context management, error correction, and possibly hybrid neuro-symbolic approaches in agentic systems.

Conclusion

This work demonstrates that the perceived diminishing returns in LLM scaling are an illusion when considering long-horizon execution. Marginal improvements in step accuracy can yield exponential gains in the length of tasks that models can reliably complete. Execution, rather than reasoning or planning, is the primary challenge for long-horizon tasks, and is subject to a self-conditioning effect that is not mitigated by scaling. Sequential test-time compute ("thinking") is essential for overcoming these limitations. These insights have significant implications for the design, evaluation, and deployment of LLM-based agents, and point to new directions for research in reliable, long-horizon AI systems.