StoxLSTM: A Stochastic Extended Long Short-Term Memory Network for Time Series Forecasting (2509.01187v1)

Abstract: The Extended Long Short-Term Memory (xLSTM) network has attracted widespread research interest due to its enhanced capability to model complex temporal dependencies in diverse time series applications. Despite its success, there is still potential to further improve its representational capacity and forecasting performance, particularly on challenging real-world datasets with unknown, intricate, and hierarchical dynamics. In this work, we propose a stochastic xLSTM, termed StoxLSTM, that improves the original architecture into a state space modeling framework by incorporating stochastic latent variables within xLSTM. StoxLSTM models the latent dynamic evolution through specially designed recurrent blocks, enabling it to effectively capture the underlying temporal patterns and dependencies. Extensive experiments on publicly available benchmark datasets from multiple research communities demonstrate that StoxLSTM consistently outperforms state-of-the-art baselines with better robustness and stronger generalization ability.

• The paper introduces a stochastic state space extension of xLSTM that integrates latent Gaussian variables to capture uncertainty and complex dependencies in time series.
• The methodology employs variational inference with patching and channel independence, achieving significant metrics improvements, including up to 26.5% lower MSE on benchmark datasets.
• The approach demonstrates efficient long-sequence modeling with O(C(L+T)) complexity, offering a scalable and robust framework for probabilistic forecasting.

StoxLSTM: A Stochastic State Space Extension of xLSTM for Time Series Forecasting

Introduction

StoxLSTM introduces a stochastic state space modeling (SSM) framework into the Extended Long Short-Term Memory (xLSTM) architecture, addressing the limitations of deterministic recurrent models in capturing the inherent uncertainty and complex latent dynamics of real-world time series. By embedding stochastic latent variables directly within the xLSTM recurrent units, StoxLSTM enables explicit modeling of non-deterministic temporal dependencies, enhancing both representational capacity and forecasting robustness across diverse domains.

Model Architecture and Methodology

Stochastic Recurrent Unit Design

StoxLSTM extends the xLSTM cell by introducing a latent state $z_t$ at each time step, sampled from a Gaussian distribution parameterized by the current hidden state $h_t$ and the previous latent state $z_{t-1}$. This stochasticization is applied to both the stabilized LSTM (sLSTM) and memory LSTM (mLSTM) blocks, as illustrated below.

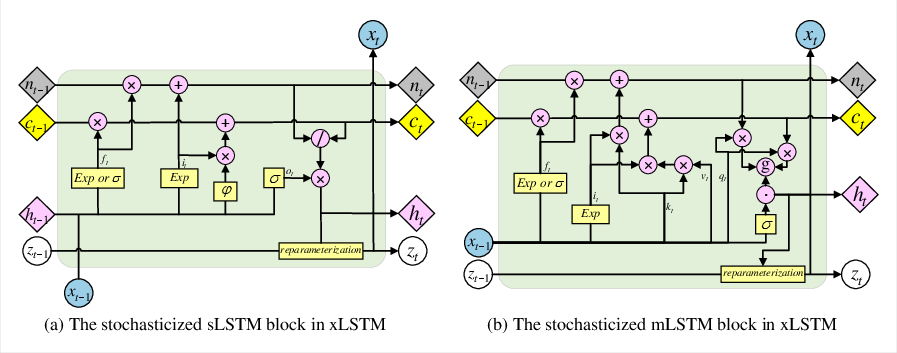
Figure 1: The recurrent unit of StoxLSTM, showing the integration of stochastic latent variables into sLSTM and mLSTM blocks.

The generative process at each time step is:

• $$z_t \sim \mathcal{N}(\mu_\theta(h_t, z_{t-1}), \sigma_\theta(h_t, z_{t-1}))$$
• $x_t = \varphi(w_z^T z_t + r_z h_t + b_z)$

This design enables the model to sample diverse future trajectories, capturing both aleatoric and epistemic uncertainty.

State Space Model Formulation

StoxLSTM is formulated as a deep SSM, where the joint distribution over observations and latent states factorizes according to Markovian and non-autoregressive assumptions:

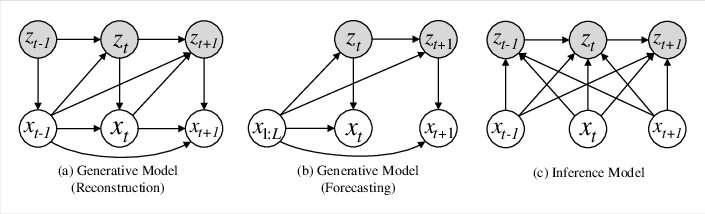
Figure 2: State space models for the generative and inference processes in StoxLSTM.

The generative model factorizes as:

$$p_\theta(x_{1:L+T}, z_{1:L+T} | x_{1:L}) = \prod_{t=1}^{L+T} p_\theta(x_t | z_t, \cdot) p_\theta(z_t | z_{t-1}, \cdot)$$

where the conditioning differs for reconstruction ($t \leq L$) and forecasting ($t > L$).

The inference model employs a bidirectional recurrent network to approximate the posterior $q_\varphi(z_t | z_{t-1}, x_{1:L+T})$ during training.

Overall Framework

StoxLSTM processes multivariate time series by decomposing them into channel-independent univariate sequences, each handled by a separate StoxLSTM module. Sequences are further divided into patches to facilitate efficient long-sequence modeling and reduce memory overhead.

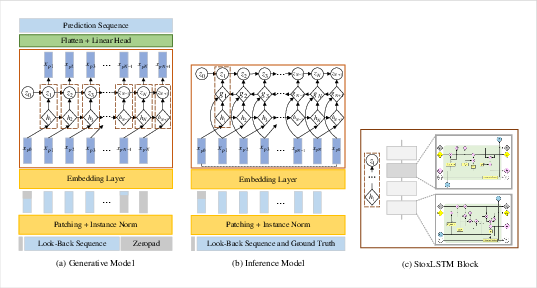
Figure 3: Overall framework of StoxLSTM, including patching, channel independence, and the stochastic recurrent backbone.

Training Objective

The model is trained via variational inference, maximizing the evidence lower bound (ELBO) on the log-likelihood of the observed sequence. The loss combines reconstruction error (MSE) and the KL divergence between the approximate posterior and the generative prior over latent states, with a $\beta$-weighting to control regularization strength.

Empirical Evaluation

Datasets and Baselines

StoxLSTM is evaluated on 9 long-term and 4 short-term public time series datasets, spanning electricity, weather, solar, traffic, and epidemiological domains. Baselines include state-of-the-art Transformer-based (Informer, Autoformer, Crossformer, FEDformer, PatchTST, iTransformer), linear (Dlinear, TimeMixer++), and xLSTM-based (xLSTMTime, P-sLSTM, xLSTM-Mixer) models.

Forecasting Performance

StoxLSTM consistently achieves the lowest MSE, MAE, and CRPS across nearly all datasets and prediction horizons. For example, on the Weather dataset, StoxLSTM reduces average MSE by 26.5% compared to xLSTM-Mixer. On the Electricity dataset, it achieves a 9.1% lower average MSE. In short-term traffic forecasting, StoxLSTM outperforms the best linear baseline (TimeMixer++) by 19.5% in MAE and 26.1% in RMSE.

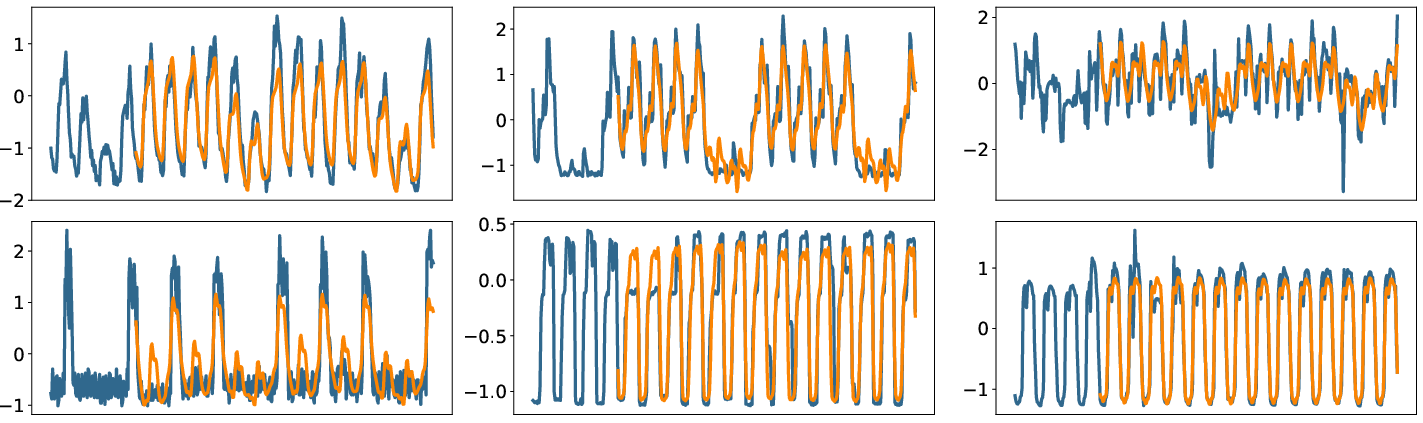
Figure 4: StoxLSTM forecasts (orange) vs. ground truth (blue) on the Electricity dataset, prediction horizon 336.

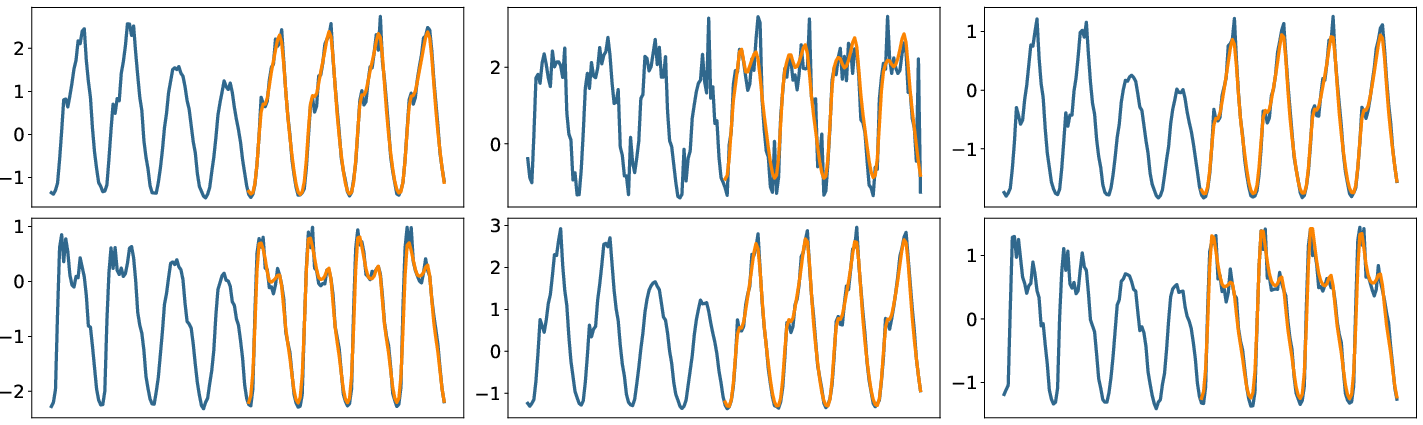
Figure 5: StoxLSTM forecasts (orange) vs. ground truth (blue) on the Traffic dataset, prediction horizon 96.

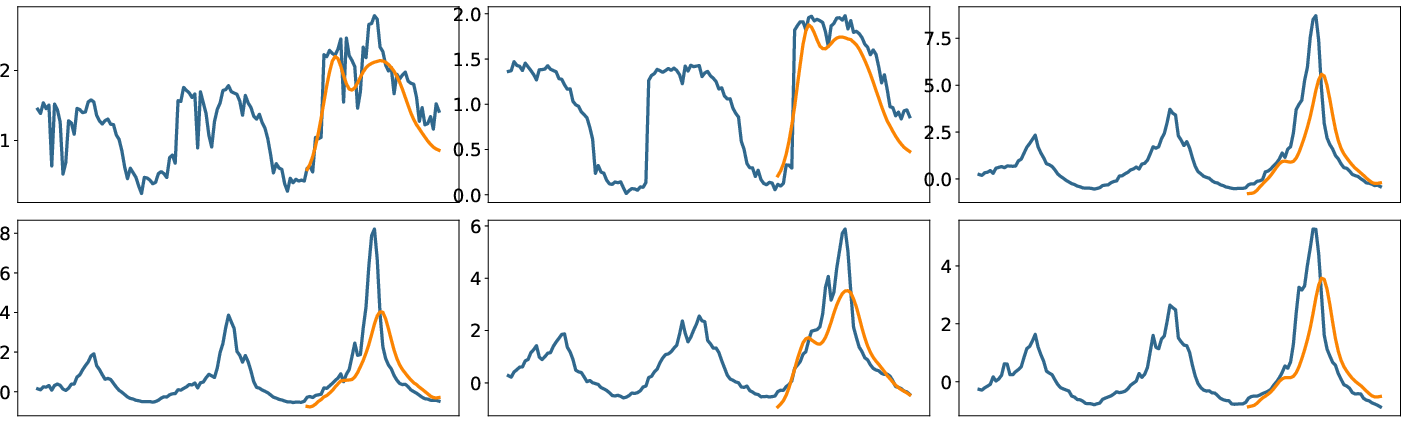
Figure 6: StoxLSTM forecasts (orange) vs. ground truth (blue) on the ILI dataset, prediction horizon 48.

Ablation and Model Analysis

Ablation studies confirm the additive benefits of patching, channel independence, series decomposition, stochastic latent variables, and the SSM structure. Removing stochasticity or SSM structure degrades performance, especially in long-horizon settings. Patching and channel independence are critical for stable training and scalability to long sequences.

Latent state analysis via heatmaps demonstrates that the learned $z_t$ encodes temporally consistent yet feature-distinct representations, supporting both accurate and robust forecasting.

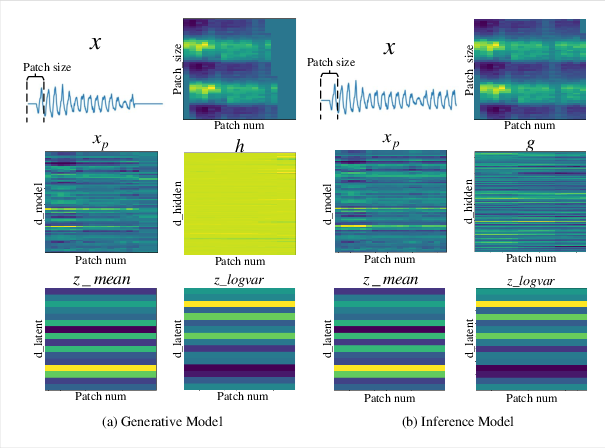
Figure 7: Heatmaps of $x$, $x_p$, $z$, and $h$ tensors from StoxLSTM, illustrating the structure and variability of latent and hidden representations.

Computational Considerations

StoxLSTM maintains $O(C(L+T))$ time complexity and $O(1)$ space complexity per channel, with efficient inference since only the generative model is required at test time. The model is competitive with, and often more efficient than, Transformer-based approaches for long sequences, though parameter count remains substantial due to the recurrent and stochastic components.

Implications and Future Directions

StoxLSTM demonstrates that integrating stochastic latent dynamics into recurrent architectures yields substantial gains in both accuracy and robustness for time series forecasting, particularly in settings with complex, nonlinear, and uncertain temporal dependencies. The explicit SSM formulation enables principled probabilistic forecasting and uncertainty quantification, which is critical for high-stakes applications in energy, finance, and healthcare.

Theoretically, this work bridges deterministic RNNs and deep generative SSMs, providing a unified framework for modeling both observed and latent temporal structure. Practically, StoxLSTM's modular design (patching, channel independence, stochasticization) facilitates adaptation to high-dimensional, multivariate, and long-horizon forecasting tasks.

Future research may focus on:

• Reducing parameter count and improving computational efficiency via parameter sharing or low-rank approximations.
• Extending the framework to handle missing data, irregular sampling, or exogenous variables.
• Exploring alternative variational objectives or richer latent variable distributions for improved expressivity.
• Integrating with recent advances in state space sequence modeling (e.g., Mamba) for further scalability.

Conclusion

StoxLSTM advances the state of the art in time series forecasting by embedding stochastic latent variables within the xLSTM architecture under a state space modeling framework. Empirical results across a wide range of benchmarks demonstrate consistent improvements in accuracy, robustness, and uncertainty quantification over deterministic and Transformer-based baselines. The approach provides a principled and practical foundation for future developments in probabilistic sequence modeling.