LLM-Integrated Bayesian State Space Models for Multimodal Time-Series Forecasting (2510.20952v1)

Abstract: Forecasting in the real world requires integrating structured time-series data with unstructured textual information, but existing methods are architecturally limited by fixed input/output horizons and are unable to model or quantify uncertainty. We address this challenge by introducing LLM-integrated Bayesian State space models (LBS), a novel probabilistic framework for multimodal temporal forecasting. At a high level, LBS consists of two components: (1) a state space model (SSM) backbone that captures the temporal dynamics of latent states from which both numerical and textual observations are generated and (2) a pretrained LLM that is adapted to encode textual inputs for posterior state estimation and decode textual forecasts consistent with the latent trajectory. This design enables flexible lookback and forecast windows, principled uncertainty quantification, and improved temporal generalization thanks to the well-suited inductive bias of SSMs toward modeling dynamical systems. Experiments on the TextTimeCorpus benchmark demonstrate that LBS improves the previous state-of-the-art by 13.20% while providing human-readable summaries of each forecast. Our work is the first to unify LLMs and SSMs for joint numerical and textual prediction, offering a novel foundation for multimodal temporal reasoning.

• The paper presents LBS, integrating LLMs with Bayesian SSMs to enable flexible multimodal forecasting with robust uncertainty quantification.
• It demonstrates a 13.20% improvement on numeric forecasting benchmarks while delivering coherent textual outputs across diverse domains.
• The model leverages latent state dynamics to capture seasonal trends and provide transparent error diagnosis for risk-aware decision-making.

LLM-Integrated Bayesian State Space Models for Multimodal Time-Series Forecasting

The paper "LLM-Integrated Bayesian State Space Models for Multimodal Time-Series Forecasting" presents an innovative approach combining LLMs with probabilistic state space models (SSMs), offering notable advancements in the domain of time-series forecasting. This integration harnesses the benefits of LLMs in processing textual data and SSMs in managing temporal uncertainties, creating a hybrid multimodal forecasting framework termed LBS.

Introduction

Multimodal time-series forecasting is a vital area where structured numeric data is often supplemented by textual information. Traditional methods have struggled with fixed input/output horizons and limited modeling of uncertainty. LBS addresses these concerns by integrating LLMs into Bayesian SSMs, allowing for flexible prediction horizons and comprehensive uncertainty quantification. This architecture combines two components: an SSM backbone handling latent state dynamics for numeric and textual data, and a pretrained LLM adapting to encode and decode textual inputs relative to these states.

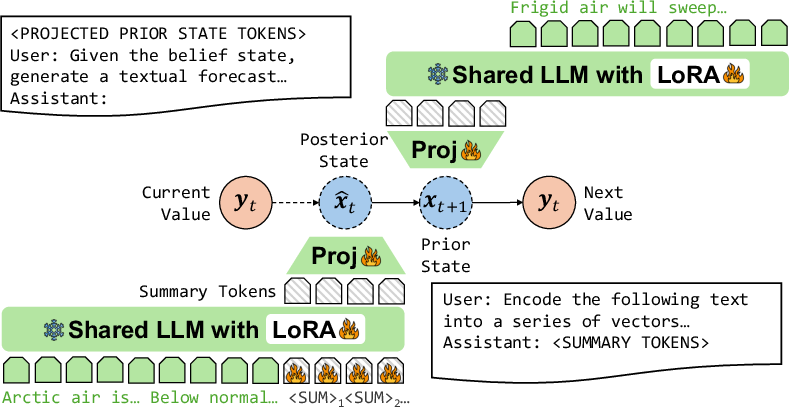
Figure 1: An illustration of the LBS architecture under for a single-step forecasting scenario.

Architectural Overview

Bayesian State Space Framework

The backbone of LBS is a probabilistic SSM that captures latent state dynamics, facilitating the generation of both numeric and textual observations. The numeric emission model produces Gaussian-distributed predictions, optimized through mean squared error minimization. Text modeling leverages LLMs, allowing coherent semantic information to guide generation processes.

Challenges in Integration

The integration of LLMs with SSMs involves text-conditioned posterior state estimation and latent state-conditioned text generation. For the former, LLMs are adapted to summarize text inputs into summary tokens, facilitating Bayesian filtering. For the latter, LLMs use latent state trajectories to produce temporally grounded textual forecasts. This dual approach incorporates multimodal instruction tuning and context compression.

Experimental Analysis

Performance Compared to Baselines

LBS demonstrates superior performance over existing models like TSFLib and HybridMMF on the TextTimeCorpus benchmark, with average improvements of 13.20% in numeric forecasting. The multimodal framework provides coherence in textual outputs while refining numeric predictions across various domains like climate and medical data.

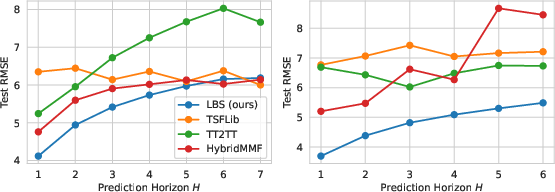
Figure 2: Test RMSE results from TTC-Climate (left) and TTC-Medical (right).

Uncertainty Quantification

LBS allows for the direct measurement of prediction variance, offering meaningful uncertainty intervals that align with real-world data fluctuations. This is particularly evident in seasonal variability, making LBS valuable for risk-aware decision-making scenarios.

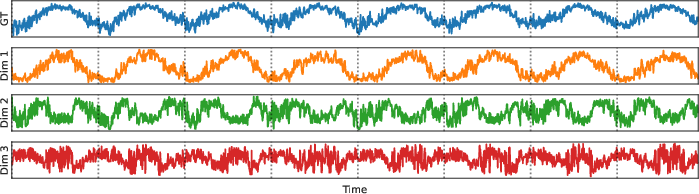
Figure 3: Visualization of ground-truth signals and three t-SNE components of the state trajectory during training on TTC-Climate.

Latent State Dynamics

The latent states exhibit strong seasonal periodicity, encoded in low-dimensional embeddings that match the trends of target values. This transparency supports model validation and error diagnosis, enhancing interpretability for stakeholders in high-stakes fields.

Scaling Impacts

Contrary to expectations, larger LLMs do not uniformly improve forecasting performance. The size increase can introduce bottlenecks within the SSM framework, indicating that further architectural tuning or alternative training techniques may be needed to fully leverage larger models.

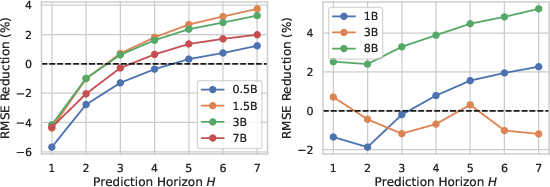
Figure 4: Test RMSE reductions of LBS relative to its unimodal counterpart on TTC-Climate with varying LLMs from the Qwen2.5 (left) and LLaMA3 (right) series.

Conclusion

LBS advances the field of multimodal time-series forecasting by effectively integrating textual and numeric data through Bayesian state spaces informed by LLMs. The framework improves upon previous methods by providing robust predictions and human-readable explanations without sacrificing uncertainty estimation. Future work should explore enhancements in SSM capacity and training methodologies to optimize LLM scaling effects.

Overall, LBS represents a significant step toward dynamic, interpretable, and reliable forecasting models capable of addressing real-world challenges in diverse application areas.