- The paper introduces LinOSS, a novel approach that leverages forced second-order ODEs to enable stable oscillatory sequence modeling.
- It employs implicit and implicit-explicit discretizations ensuring global stability and time reversibility for efficient computation.
- Empirical evaluations show LinOSS outperforms state-of-the-art models in tasks like long-range classification, forecasting, and regression.
LinOSS: A Novel Approach to Sequence Modeling with Oscillatory State-Space Models
The paper introduces Linear Oscillatory State-Space models (LinOSS), a novel approach to sequence modeling that leverages stable discretizations of forced linear second-order ordinary differential equations (ODEs) to model oscillators. The model distinguishes itself through several key properties, including provable stability with nonnegative diagonal state matrices, symplectic discretization for time reversibility, and universality as an approximator of continuous and causal operators between time-series. Empirical evaluations demonstrate that LinOSS consistently matches or outperforms state-of-the-art sequence models on a wide range of tasks.
The LinOSS model is based on the following system of forced linear second-order ODEs:
x′′(t)=−Ωx(t)+Bu(t)+b, y(t)=Cx(t)+Du(t),
where x(t)∈Rm is the hidden state, y(t)∈Rq is the output state, u(t)∈Rp is the time-dependent input signal, and Ω∈Rm×m, B∈Rm×p, C∈Rq×m, D∈Rq×p, and b∈Rm are weights and biases. A crucial aspect of this formulation is that Ω is a diagonal matrix with nonnegative entries, which ensures stable dynamics.
To facilitate efficient computation, the second-order ODE is converted into a first-order system by introducing an auxiliary state v(t)∈Rm, with v=x′:
x′(t)=v(t), v′(t)=−Ωx(t)+Bu(t).
Discretization Schemes and Stability
The paper introduces two discretization schemes: implicit time integration (LinOSS-IM) and implicit-explicit time integration (LinOSS-IMEX).
Implicit Time Integration (LinOSS-IM)
The implicit discretization is given by:
xn=xn−1+Δt(vn), vn=vn−1+Δt(−Ωxn+Bun),
where Δt is the timestep. This discretization is shown to yield globally asymptotically stable dynamics, provided that Ω is a nonnegative diagonal matrix.
Implicit-Explicit Time Integration (LinOSS-IMEX)
The implicit-explicit discretization is given by:
xn=xn−1+Δt(vn), vn=vn−1+Δt(−Ωxn−1+Bun).
This scheme is symplectic, meaning it preserves a Hamiltonian close to that of the continuous system. Consequently, it conserves the symmetry of time reversibility, leading to memory-efficient implementations via backpropagation through time.
Fast Recurrence via Associative Parallel Scans
To accelerate training and inference, LinOSS employs associative parallel scans. This technique reduces the computational time of recurrent operations from O(N) to O(log2(N)), where N is the sequence length.
The associative operation is defined as:
(A1,B1)∙(A2,B2)=(A1A2,A1B2+B1),
where A represents the hidden-to-hidden weight matrix and B represents the input transformation. This operation is applied to both the implicit and implicit-explicit discretizations, enabling efficient computation of the recurrent dynamics.
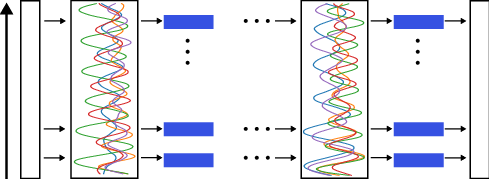
Figure 1: Schematic drawing of the proposed Linear Oscillatory State-Space model (LinOSS). The input sequences are processed through multiple LinOSS blocks. Each block is composed of a LinOSS layer followed by a nonlinear transformation, specifically a Gated Linear Units \citep{glu} (GLU) layer in our case. After passing through several LinOSS blocks, the latent sequences are decoded to produce the final output sequence.
Theoretical Properties
The paper provides rigorous theoretical analysis of LinOSS, demonstrating its stability, capacity for learning long-range interactions, and universality as an approximator.
Stability
It is proven that LinOSS-IM exhibits asymptotically stable dynamics for any nonnegative diagonal matrix Ω. This contrasts with previous state-space models that require heavily constrained parameterizations. LinOSS-IMEX, on the other hand, features eigenvalues with a magnitude of 1 which allows for learning interactions over arbitrarily long sequences.
Universality
LinOSS is proven to be a universal approximator of continuous and causal operators between time-series. This result indicates that LinOSS can express complex mappings between general input and output sequences, not necessarily limited to oscillatory patterns. The proof relies on encoding the infinite-dimensional operator with a finite-dimensional operator that utilizes the structure of the LinOSS ODE system.
Empirical Evaluation
The LinOSS models were evaluated on a range of sequence modeling tasks, including long-range classification, regression, and long-horizon forecasting. The empirical results demonstrate that LinOSS consistently matches or outperforms state-of-the-art models, including Mamba, LRU, and S5.
Long-Range Interactions
On the UEA Multivariate Time Series Classification Archive, LinOSS-IM achieved state-of-the-art results, particularly on datasets with long sequences such as EigenWorms, improving the test accuracy from 85% to 95%.
Extreme Length Sequences
On the PPG-DaLiA dataset, LinOSS models significantly outperformed other models, with LinOSS-IM exhibiting nearly a 2x improvement over Mamba and a 2.5x improvement over LRU.
Long-Horizon Forecasting
On a weather prediction task, LinOSS models outperformed Transformer-based baselines and other state-space models in forecasting future climate variables.
Conclusion
The LinOSS model represents a significant advancement in sequence modeling, offering a combination of theoretical rigor and empirical performance. Its stable dynamics, symplectic discretization, and universality make it a promising architecture for a wide range of applications. The empirical results demonstrate that LinOSS can effectively model long-range interactions and achieve state-of-the-art performance on challenging real-world datasets.
Future research directions may include exploring different parameterizations of the diagonal weight matrix Ω, incorporating adaptive time-stepping schemes, and applying LinOSS to other modalities such as audio and video.
