The Nondecreasing Rank (2509.00265v1)

Abstract: In this article the notion of the nondecreasing (ND) rank of a matrix or tensor is introduced. A tensor has an ND rank of r if it can be represented as a sum of r outer products of vectors, with each vector satisfying a monotonicity constraint. It is shown that for certain poset orderings finding an ND factorization of rank $r$ is equivalent to finding a nonnegative rank-r factorization of a transformed tensor. However, not every tensor that is monotonic has a finite ND rank. Theory is developed describing the properties of the ND rank, including typical, maximum, and border ND ranks. Highlighted also are the special settings where a matrix or tensor has an ND rank of one or two. As a means of finding low ND rank approximations to a data tensor we introduce a variant of the hierarchical alternating least squares algorithm. Low ND rank factorizations are found and interpreted for two datasets concerning the weight of pigs and a mental health survey during the COVID-19 pandemic.

• The paper introduces nondecreasing rank as a generalization of nonnegative rank by incorporating monotonicity constraints in matrix and tensor factorizations.
• It develops detailed geometric characterizations of order cones and offers explicit representations and a HALS algorithm for efficient low-ND-rank approximations.
• Applications to pig weight data and mental health surveys demonstrate the practical interpretability and utility of ND factorizations in structured data analysis.

The Nondecreasing Rank: Theory, Geometry, and Applications

Introduction

This paper introduces and develops the theory of the nondecreasing (ND) rank for matrices and tensors, a generalization of nonnegative rank that incorporates monotonicity constraints with respect to user-specified partial orders (posets) on the tensor modes. The ND rank is defined as the minimal number of rank-one outer products of vectors, each constrained to be nondecreasing with respect to the poset, required to represent a given tensor. The work provides a comprehensive treatment of the algebraic, geometric, and algorithmic properties of ND rank, including its relationship to nonnegative rank, the geometry of the associated order cones, explicit characterizations of extremal rays, and practical algorithms for low-ND-rank approximation. Theoretical results are complemented by applications to real datasets, demonstrating the interpretability and utility of ND factorizations in structured data analysis.

Definition and Motivation

The ND rank extends the classical nonnegative rank by imposing additional monotonicity constraints on the factors. For a tensor $T$ indexed by a product of posets $P = P_1 \times \cdots \times P_k$, the ND rank is the smallest $r$ such that

$$T = \sum_{i=1}^r v^{(i,1)} \otimes \cdots \otimes v^{(i,k)}, \quad v^{(i,j)} \in C(P_j)$$

where $C(P_j)$ is the order cone of nonnegative, nondecreasing functions on $P_j$. This formulation is motivated by applications where monotonicity is a natural structural constraint, such as dose-response experiments, longitudinal growth data, and order-restricted inference.

The ND rank is always at least the nonnegative rank, but can be strictly larger, especially when the poset structure is nontrivial. The paper provides explicit examples and geometric intuition for this phenomenon.

Geometry of Order Cones and Existence of ND Factorizations

A central technical contribution is the detailed analysis of the order cone $C(P)$, the set of nonnegative, nondecreasing functions on a finite poset $P$. The extremal rays of $C(P)$ are characterized as indicator functions of connected upsets in $P$. The geometry of $C(P)$ is shown to depend critically on the presence of colliders (nodes with multiple parents) in the Hasse diagram of $P$.

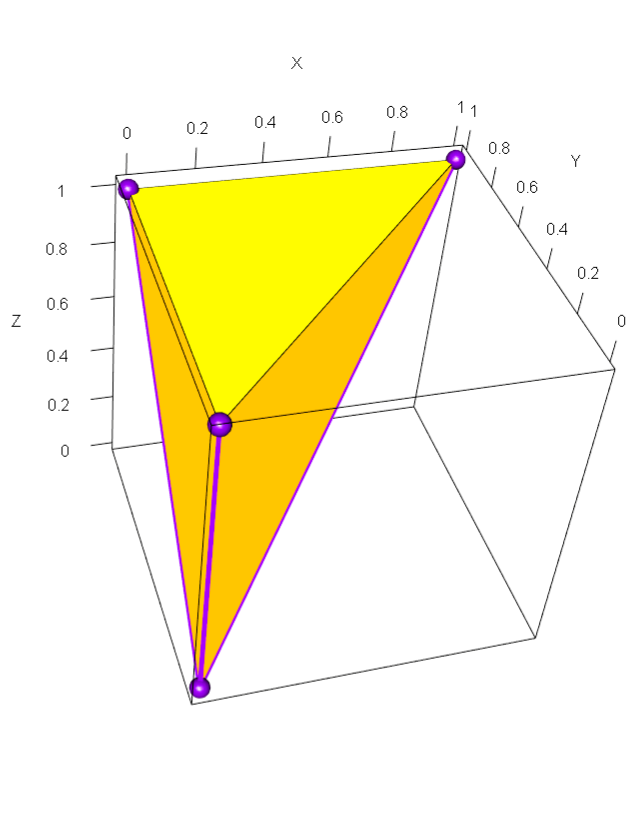
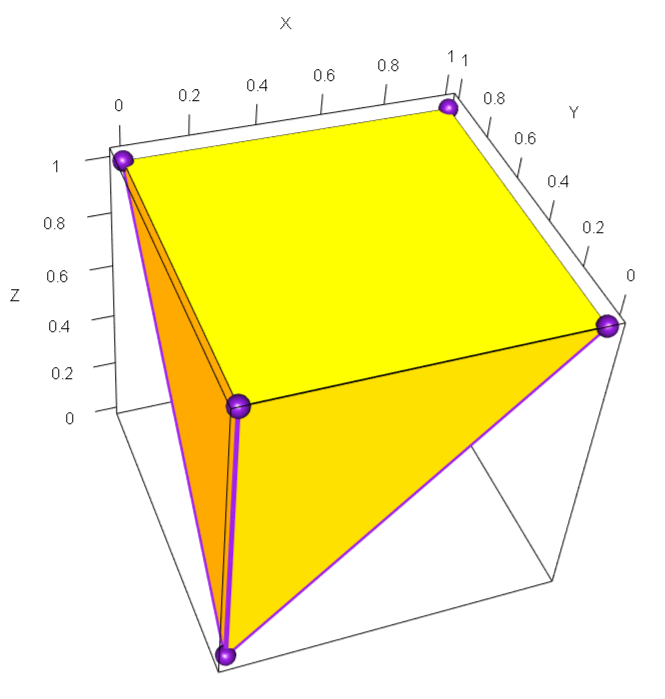
Figure 2: Order polytope of $Z \prec Y \prec X$.

If $P$ is a union of trees (i.e., has no colliders), $C(P)$ is a simplicial cone, linearly equivalent to the nonnegative orthant. In this case, the ND rank coincides with the nonnegative rank up to a linear change of coordinates, and the existence of ND factorizations is guaranteed for all monotone tensors. In contrast, for posets with colliders, $C(P)$ is not simplicial, and there exist monotone tensors with infinite ND rank.

The projective tensor product of order cones is analyzed, and the extremal rays of the ND cone are shown to be tensor products of extremal rays of the constituent order cones. The paper provides explicit $V$- and $H$-representations for these cones, enabling algorithmic membership testing and construction of ND factorizations.

Reduction to Nonnegative Rank and M\"obius Inversion

For simplicial order cones, the ND rank problem can be reduced to a nonnegative rank problem via an explicit invertible linear transformation, constructed from the M\"obius inversion of the poset. This reduction is formalized as follows: if $A_j$ maps $C(P_j)$ to the nonnegative orthant, then

$$\mathrm{NDrank}(T) = \mathrm{rank}_+\left( (A_1 \otimes \cdots \otimes A_k) T \right)$$

This equivalence enables the transfer of algorithmic and theoretical results from nonnegative rank to ND rank in the tree-ordered case.

The M\"obius transform is shown to have a probabilistic interpretation: for a probability mass function $R$ on $P$, the M\"obius transform yields the multivariate CDF, and the ND rank of the CDF equals the nonnegative rank of the PMF.

Maximum and Typical ND Ranks

The paper establishes upper and lower bounds for the maximum ND rank in various settings. For order cones with $q_j$ extremal rays, the maximum ND rank in the tensor product is at most $\prod_{j=1}^{k-1} q_j$. When one of the cones is simplicial, this bound is tight and equals $\min(q_1, q_2)$ in the matrix case. For posets with collider structure, the maximum ND rank can be exponentially larger, e.g., $2^{p-1}$ for a $p$-element collider poset.

The set of typical ND ranks (ranks that occur with positive probability in the cone) is completely characterized: for matrices, all ranks between the minimal typical real rank and the maximum ND rank are typical. Notably, the set of typical ND ranks can be much larger than in the nonnegative or real case.

ND Rank One and Two

A key structural result is that for rank-one and rank-two matrices, the ND rank coincides with the usual rank, provided the matrix is monotone. This extends the classical result for nonnegative rank and provides explicit semialgebraic characterizations for ND rank-one and rank-two sets.

Border ND Rank and Optimization

The ND rank cone $N_{\leq r}$ is shown to be closed, implying that the border ND rank equals the ND rank. This is in contrast to the real rank, where the set of rank-$r$ tensors is not closed. As a consequence, optimization problems over $N_{\leq r}$, such as best low-ND-rank approximation, always admit a solution.

The paper develops a hierarchical alternating least squares (HALS) algorithm for ND rank approximation, leveraging the separability of the quadratic objective and the pool-adjacent-violators algorithm (PAVA) for isotonic regression. The algorithm is a block coordinate descent method, with each update efficiently solved via PAVA. The method is applicable to a variety of loss functions, including Frobenius norm and likelihood-based divergences for exponential family models.

Applications

Two real-world applications are presented:

1. Pig Weight Data: The ND rank-two approximation of longitudinal pig weight data yields interpretable monotone growth curves for subpopulations, with individual pigs' growth modeled as conical combinations of these curves. The ND factorization provides more interpretable components than unconstrained or nonnegative factorizations.

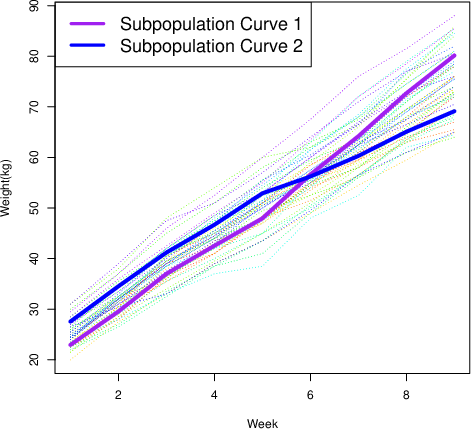
Figure 4: Observed growth curves for each pig, along with the two subpopulation growth curves ${b}^{(1)}$ and ${b}^{(2)}$.

1. Canadian Mental Health Survey: A three-way ND factorization of survey data (age, year, gender) reveals interpretable patterns in perceived mental health, with clear separation of gender effects and temporal trends, especially during the COVID-19 pandemic. The ND rank-two decomposition succinctly captures the main structure and interactions in the data.

Implications and Future Directions

The introduction of ND rank opens new avenues for structured low-rank modeling in settings where monotonicity is a natural constraint. The geometric analysis of order cones and the explicit reduction to nonnegative rank in tree-ordered cases provide a solid foundation for both theoretical and algorithmic developments. The HALS algorithm and its variants enable practical computation of ND factorizations in high-dimensional settings.

Potential future directions include:

• Development of efficient multiplicative update algorithms for ND rank, extending the NMF literature to the monotone setting.
• Investigation of uniqueness and identifiability conditions for ND factorizations, possibly leveraging separability or minimum/maximum volume criteria.
• Extension to other shape constraints (e.g., convexity, unimodality) and infinite-dimensional functional data.
• Application to order-restricted inference, causal modeling, and structured latent variable models.

Conclusion

The ND rank provides a principled and flexible framework for low-rank modeling under monotonicity constraints, with strong theoretical guarantees and practical interpretability. The geometric and algorithmic tools developed in this work lay the groundwork for further advances in structured tensor factorization and order-constrained statistical inference.