Modular Arithmetic: Language Models Solve Math Digit by Digit (2508.02513v1)

Abstract: While recent work has begun to uncover the internal strategies that LLMs employ for simple arithmetic tasks, a unified understanding of their underlying mechanisms is still lacking. We extend recent findings showing that LLMs represent numbers in a digit-wise manner and present evidence for the existence of digit-position-specific circuits that LLMs use to perform simple arithmetic tasks, i.e. modular subgroups of MLP neurons that operate independently on different digit positions (units, tens, hundreds). Notably, such circuits exist independently of model size and of tokenization strategy, i.e. both for models that encode longer numbers digit-by-digit and as one token. Using Feature Importance and Causal Interventions, we identify and validate the digit-position-specific circuits, revealing a compositional and interpretable structure underlying the solving of arithmetic problems in LLMs. Our interventions selectively alter the model's prediction at targeted digit positions, demonstrating the causal role of digit-position circuits in solving arithmetic tasks.

• The paper reveals that LLMs process arithmetic digit by digit using modular circuits distributed across model layers.
• It employs Fisher Score-based feature selection and causal intervention to validate neuron groups responsible for specific digit positions.
• Experiments on the LLaMA3-8B model show that roughly 60% of neurons engage in distinct arithmetic tasks, demonstrating non-overlapping circuit functionality.

Modular Arithmetic: LLMs Solve Math Digit by Digit

The paper "Modular Arithmetic: LLMs Solve Math Digit by Digit" (2508.02513) explores digit-position-specific circuits in LLMs that facilitate arithmetic operations. The authors present a comprehensive analysis of these circuits using Feature Importance and Causal Interventions to demonstrate how LLMs solve arithmetic tasks, transcending simple heuristic-based approaches and revealing structured and modular arithmetic processes.

Digit-Position Circuits

The investigation identifies modular subgroups of MLP neurons that independently generate results for specific digit positions across multiple layers. These circuits entail sets of neurons responsible for arithmetic subtasks partitioned by digit positions (units, tens, hundreds), enabling parallel and independent calculations. This is illustrated by the model's ability to solve the arithmetic problem 347 + 231 by independently computing 7+1 for units, 4+3 for tens, and 3+2 for hundreds.

Figure 1: Main finding: Simple arithmetic tasks are solved modularly by digit-position-specific circuits distributed across multiple MLP layers. Distinct sets of MLP neurons are responsible for generating results digits in parallel and independently for different positions.

Methodology

Feature Selection and Causality

The authors employ Fisher Score-based feature selection to identify neurons primarily responsible for specific digit-position calculations. This involves measuring neuron sensitivity to arithmetic subtasks across different positions to determine their roles in arithmetic processes. The team performed causal intervention by manipulating neuron activations to validate these circuits' roles in solving arithmetic problems.

Figure 2: Intervening on only the MLP neurons that are members of one of the digit-position specific circuits results in targeted changes only on the corresponding digit-position of the generated result. Here, an intervention on the unit position circuit only affects the unit position of the generated result.

Dataset and Model Analysis

Datasets for addition and subtraction tasks were constructed to isolate digit-wise computations without carry operations. The study evaluated several transformer models, focusing on LLaMA3-8B due to its typical use of multi-digit tokenization, ensuring that observed digit-wise processing results from the model's internal complexities rather than external tokenization effects.

Findings and Results

The identification process revealed conspicuous digit-position-specific circuits substantially contributing to arithmetic subtasks across different transformer architectures. For LLaMA3-8B, approximately 60.3% of neurons in relevant layers are involved in these dedicated circuits. Notably, the circuits for the unit, tens, and hundreds digits were largely non-overlapping, indicative of the model's digit-positional modularity.

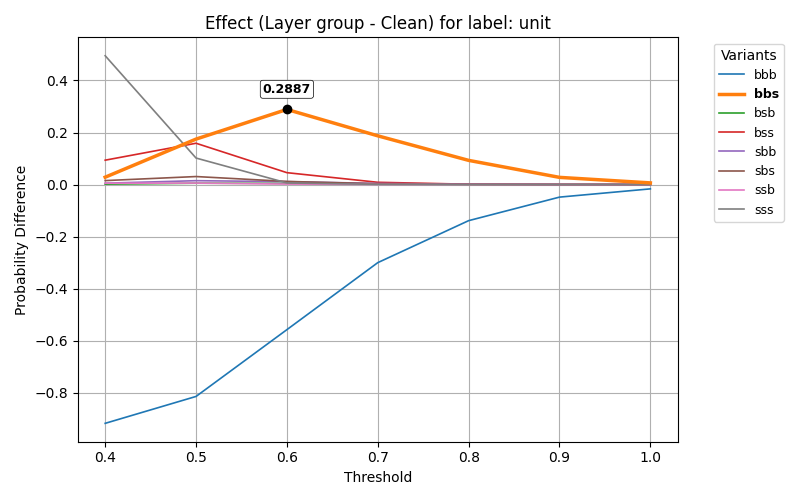
Figure 3: Effect of intervening on the unit circuit with a carry originating from unit digit position.

The causal interventions further demonstrated that altering the activation of neuron groups corresponding to a digit change solely affected that digit, leaving others unchanged. This confirms the circuits' specificity and causal involvement in arithmetic operations.

Distinguishing Circuit Characteristics

Subsequent analysis discerned that addition and subtraction circuits are largely distinct, each relying on unique neuron subsets for different arithmetic operations. Furthermore, interventions that introduced carry propagation revealed that digit-position circuits operate independently, suggesting separate mechanisms manage carry operations.

Figure 4: Effect of intervening on the tens circuit with a carry originating from tens digit position.

Implications and Future Work

This study elucidates a structured arithmetic processing framework where LLMs utilize distinct circuits for discrete digit-position calculations. These findings underscore a shift away from simple heuristic processing towards a more refined arithmetic execution approach.

Extensions for this research could include exploring more complex arithmetic operations, such as multiplication and division, and further dissecting circuits responsible for integrating digit-level computations into coherent model outputs. Additionally, investigating the roles of attention heads and other neural components could augment the understanding of arithmetic processing in LLMs.

Conclusion

The paper presents a nuanced perspective on how LLMs handle arithmetic tasks, emphasizing digit-wise, modular computation through neuron-specific circuits. These insights bolster understanding of the capacities and inherent architectural efficiencies within modern LLMs, showcasing an intricate interplay between model size, tokenization strategies, and arithmetic performance.