Do Large Language Models Truly Grasp Addition? A Rule-Focused Diagnostic Using Two-Integer Arithmetic (2504.05262v3)

Abstract: LLMs achieve impressive results on advanced mathematics benchmarks but sometimes fail on basic arithmetic tasks, raising the question of whether they have truly grasped fundamental arithmetic rules or are merely relying on pattern matching. To unravel this issue, we systematically probe LLMs' understanding of two-integer addition ($0$ to $2^{64}$) by testing three crucial properties: commutativity ($A+B=B+A$), representation invariance via symbolic remapping (e.g., $7 \mapsto Y$), and consistent accuracy scaling with operand length. Our evaluation of 12 leading LLMs reveals a stark disconnect: while models achieve high numeric accuracy (73.8-99.8%), they systematically fail these diagnostics. Specifically, accuracy plummets to $\le 7.5$% with symbolic inputs, commutativity is violated in up to 20% of cases, and accuracy scaling is non-monotonic. Interventions further expose this pattern-matching reliance: explicitly providing rules degrades performance by 29.49%, while prompting for explanations before answering merely maintains baseline accuracy. These findings demonstrate that current LLMs address elementary addition via pattern matching, not robust rule induction, motivating new diagnostic benchmarks and innovations in model architecture and training to cultivate genuine mathematical reasoning. Our dataset and generating code are available at https://github.com/kuri-leo/LLM-arithmetic-diagnostic.

• The paper demonstrates that LLMs can handle complex arithmetic yet falter on basic addition, questioning their true rule comprehension.
• The paper shows that performance drops sharply under symbolic transformations, highlighting a dependence on token-level heuristics.
• The paper reveals that while fine-tuning boosts numeric accuracy, it often fails to improve symbolic task performance, underscoring a trade-off in generalization.

Assessing Understanding of Arithmetic in LLMs: An Analysis

LLMs have demonstrated capability on sophisticated mathematical benchmarks, yet they frequently falter on basic arithmetic operations. This paper systematically investigates whether LLMs truly understand fundamental arithmetic rules or merely replicate learned patterns. The paper employs two-integer addition as a diagnostic lens to evaluate LLMs on three critical properties: commutativity, representation invariance, and scaling consistency. Insights from twelve leading LLMs reveal a predominant reliance on pattern matching rather than robust rule-based reasoning.

Diagnostic Approach and Empirical Evidence

The Paradox of Arithmetic Competence

Although LLMs excel mathematically, basic arithmetic tasks expose significant weaknesses, raising doubts about their grasp of underlying rules. The paper illustrates this paradox through a representative example: LLMs perform complex numerical calculations with ease, yet struggle with simple tasks like basic addition (Figure 1).

Figure 1: Illustration of LLM Paradox: LLMs excel at complex math but falter on basic addition, raising the question of whether they grasp rules or merely reproduce patterns. True grasp implies consistent performance and adherence to mathematical properties under novel conditions.

Performance Variability and Task Characteristics

Commutativity and Symbolic Representation

Evaluation of twelve LLM models against commutativity and symbolic representation invariance highlights systemic performance issues. Failures in these areas suggest that LLMs predominantly leverage token-level heuristics over abstracted rules, evidenced by significant accuracy drops in commutativity tests and symbolic tasks. LLMs achieving 98% numeric accuracy often see performance plummet to 7% under symbolic remapping, revealing a core reliance on familiar input patterns.

Non-Monotonic Scaling Consistency

Evidence shows non-monotonic behavior regarding operand length: accuracy inconsistently rebounds at certain digit counts instead of degrading monotonically (Figure 2). Such patterns indicate that success derives from memorized heuristics rather than scalable arithmetic understanding.

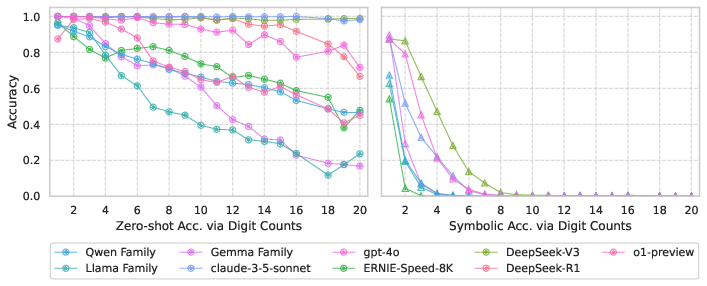
Figure 2: Performance Degradation Patterns in Zero-shot vs. Symbolic Addition. Suggests brittle pattern matching rather than true algorithmic reasoning, with systematic degradation in symbolic addition tests.

Modulating Comprehension Through Intervention

Prompt-level and Parameter-level Interventions

The paper explores interventions including explicit rule provision and fine-tuning strategies. Surprisingly, explicit rule provision degrades arithmetic performance, contradicting expected improvements (Figure 3). This degradation underscores LLMs' tuning towards token memorization.

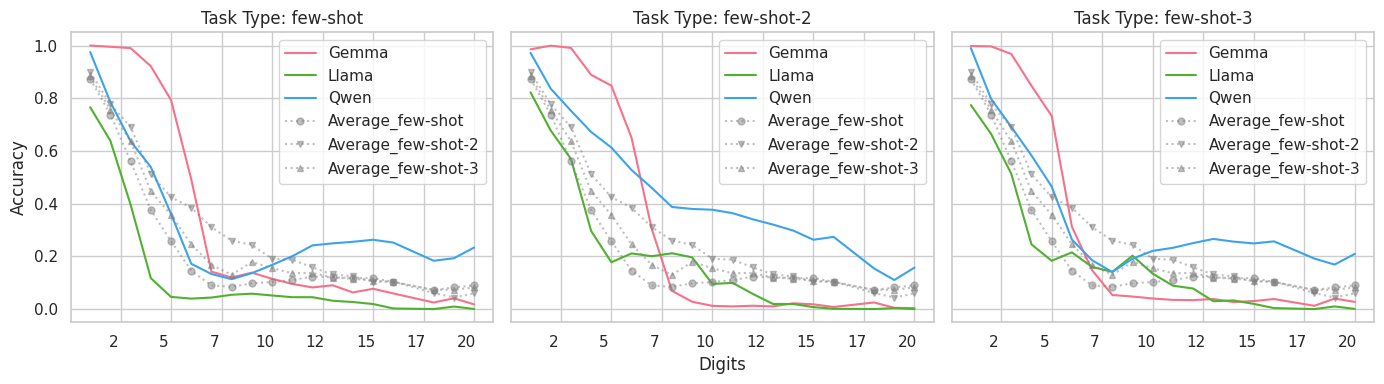
Figure 3: Few-Shot Performance with Explicit Rule Provision. This strategy drops performance compared to zero-shot, contradicting improvement expectations.

Fine-Tuning Strategies

Fine-tuning experiments reaffirm the pattern-matching characteristics in LLMs. While Supervised Fine-Tuning (SFT) enhances numeric accuracy, it shows minimal transfer to symbolic tasks, reflecting a primary optimization towards data-specific tokens. Preference Optimization (DPO) and Reinforcement Learning (RL) strategies yield better symbolic task generalization but compromise peak numeric performance, revealing trade-offs between generalization and specialization.

Implications and Future Directions

The findings underscore a significant limitation in current LLMs' arithmetic comprehension, suggesting an urgent need for new benchmarks focusing on keyword invariance, scaling consistency, and algebraic integrity. Beyond benchmarking, future model development should strive for architectures capable of abstract rule abstraction, bridging pattern reliance and genuine arithmetic reasoning. The implication is clear: without targeted evaluation efforts, prevailing benchmarks may inflate perceived LLM capabilities, overlooking foundational reasoning gaps.

Conclusion

In summary, this diagnostic paper exposes critical arithmetic understanding deficits in LLMs despite their apparent mathematical prowess. The reliance on pattern-matching over rule-based reasoning limits models' arithmetic reliability. Moving forward, research must prioritize fostering genuine mathematical abstraction in LLMs to facilitate robust, rule-consistent AI applications.