Hessian Geometry of Latent Space in Generative Models (2506.10632v1)

Abstract: This paper presents a novel method for analyzing the latent space geometry of generative models, including statistical physics models and diffusion models, by reconstructing the Fisher information metric. The method approximates the posterior distribution of latent variables given generated samples and uses this to learn the log-partition function, which defines the Fisher metric for exponential families. Theoretical convergence guarantees are provided, and the method is validated on the Ising and TASEP models, outperforming existing baselines in reconstructing thermodynamic quantities. Applied to diffusion models, the method reveals a fractal structure of phase transitions in the latent space, characterized by abrupt changes in the Fisher metric. We demonstrate that while geodesic interpolations are approximately linear within individual phases, this linearity breaks down at phase boundaries, where the diffusion model exhibits a divergent Lipschitz constant with respect to the latent space. These findings provide new insights into the complex structure of diffusion model latent spaces and their connection to phenomena like phase transitions. Our source code is available at https://github.com/alobashev/hessian-geometry-of-diffusion-models.

• The paper develops a novel geometric framework leveraging Hessian geometry and Fisher information to reconstruct latent spaces in generative models.
• It applies the method to models like Ising, TASEP, and diffusion, revealing fractal phase transitions and distinguishing smooth versus abrupt interpolations.
• Experiments highlight improved detection of phase transitions and enhanced geodesic interpolation compared to traditional dimensionality reduction techniques.

Hessian Geometry of Latent Space in Generative Models

Introduction

The paper of the latent space in generative models often reveals non-linear transitions in image appearance, particularly in state-of-the-art image generation models where interpolation across the latent space is involved. This paper explores these transitions using a geometric framework, proposing a method to analyze the latent space of generative models through the lens of Hessian geometry and the Fisher information metric. The method reconstructs the Fisher metric by approximating the posterior distribution of latent variables given generated samples and subsequently learning the log-partition function, crucial for defining the Fisher metric in exponential families.

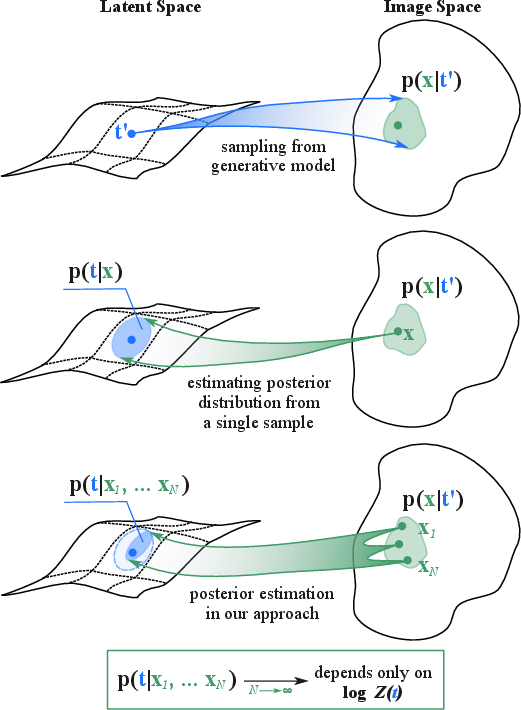
Figure 1: Visualization of Theorem with a focus on latent space geometry and log-partition function reconstruction.

Methodology

The proposed method is grounded in information geometry, particularly leveraging the properties of the Fisher information metric and Hessian geometry. The Fisher metric is reconstructed for generative models by approximating the posterior distribution $p(t|x)$ and estimating the log-partition function $\log Z(t)$. This follows theoretical guarantees provided by Theorems 3.1 and 3.2, which are validated on statistical models like Ising and TASEP, and also extended to diffusion models revealing fractal phase transitions.

Step 1: Approximating Posterior Distribution

The posterior distribution $p(t|x)$ is approximated either through direct mapping or feature extraction. For statistical systems like Ising and TASEP, U$^2$-Net is utilized to predict the probability distribution over the parameter space. In the image domain, pre-trained feature extractors such as CLIP can help approximate the posterior by computing distances between feature embeddings, acting as proxies for the KL divergence.

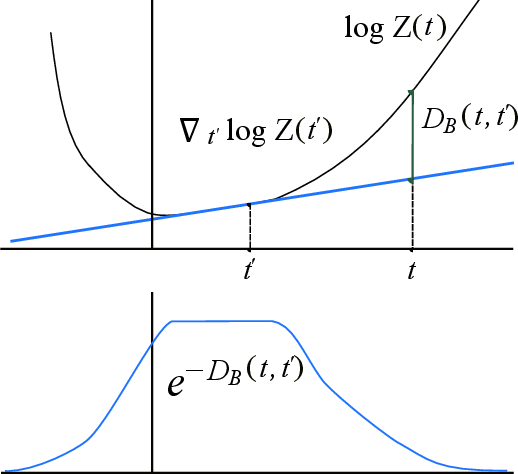
Figure 2: Visualizing Bregman divergence illustrating the connection between probabilistic structures and geometric divergences.

Step 2: Learning the Log-Partition Function

To infer the Fisher metric, a multi-layer perceptron (MLP) is trained to learn the log-partition function via minimizing the Jensen-Shannon divergence between the true posterior and the reconstructed distribution from the approximated partition function. This step ensures capturing the geometry of the latent space, especially examining the smoothness and abrupt changes characteristic of phase transitions in diffusion models.

Experiments and Results

Statistical Models: Ising and TASEP

The theoretical framework was validated using exactly solvable models. The proposed method outperformed baselines like PCA-VAE and Mean-as-Stats in terms of reconstructing free energy and its derivatives, critical for identifying phase transitions.

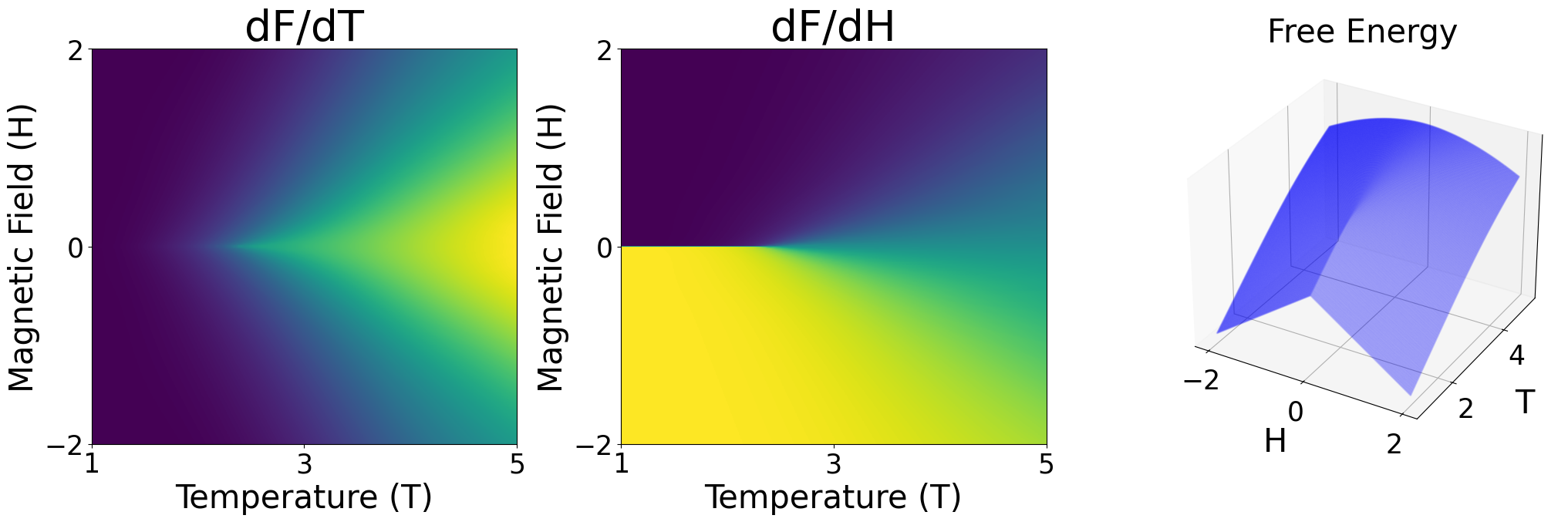
Figure 3: Partial derivatives of reconstructed free energy showcasing phase transition indicators in the Ising model.

Diffusion Models: Latent Space Phases

The method was applied to two-dimensional slices of diffusion models, revealing the fractal nature of phase boundaries and demonstrating near-linear geodesic interpolation within phases. This is in contrast to non-linear behavior at phase boundaries where Lipschitz constants diverge, correlating with perceptual discontinuities in generated outputs.

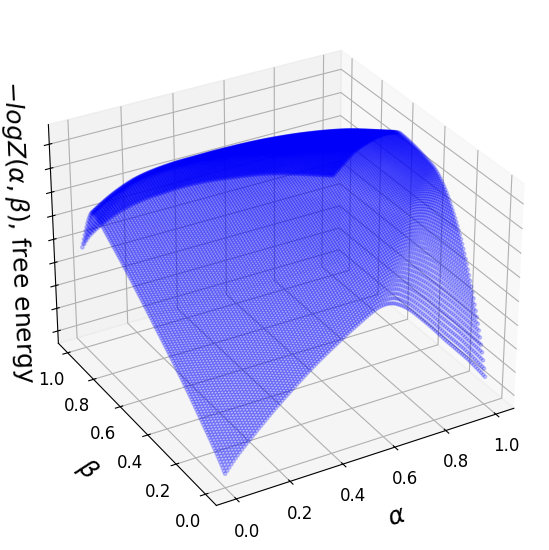
Figure 4: Free energy surface reconstruction in diffusion models, illustrating smooth and abrupt transitions.

Discussion

The paper's approach unifies concepts from statistical physics and information geometry to analyze latent spaces in generative models known for exhibiting complex behavior. The insights into phase transitions — typically resulting from discontinuous or multi-modal latent distributions — allow for improved interpolation strategies, with potential applications in more finely tuning generative processes.

The implications extend to enhancing robustness in generative models by understanding the structural properties of latent spaces, possibly informing methods to counteract issues like mode collapse or generating more semantically consistent interpolations through geodesics.

Conclusion

This research provides a geometric foundation for understanding the latent spaces of generative models, extends the applicability of geometric methods to practical image generation tasks, and highlights the presence and nature of phase transitions within these spaces. Future work could explore dynamic adjustment of sampling strategies to leverage these phase boundaries for model enhancement.