The Information Dynamics of Generative Diffusion (2508.19897v1)
Abstract: Generative diffusion models have emerged as a powerful class of models in machine learning, yet a unified theoretical understanding of their operation is still developing. This perspective paper provides an integrated perspective on generative diffusion by connecting their dynamic, information-theoretic, and thermodynamic properties under a unified mathematical framework. We demonstrate that the rate of conditional entropy production during generation (i.e. the generative bandwidth) is directly governed by the expected divergence of the score function's vector field. This divergence, in turn, is linked to the branching of trajectories and generative bifurcations, which we characterize as symmetry-breaking phase transitions in the energy landscape. This synthesis offers a powerful insight: the process of generation is fundamentally driven by the controlled, noise-induced breaking of (approximate) symmetries, where peaks in information transfer correspond to critical transitions between possible outcomes. The score function acts as a dynamic non-linear filter that regulates the bandwidth of the noise by suppressing fluctuations that are incompatible with the data.
Sponsor
Paper Prompts
Sign up for free to create and run prompts on this paper using GPT-5.
Top Community Prompts
Explain it Like I'm 14
A simple explanation of “The Information Dynamics of Generative Diffusion”
What is this paper about?
This paper tries to answer a big question: how do modern diffusion models (the kind that turn random noise into images, sounds, or text) actually work, viewed through the lenses of motion (dynamics), information (how uncertainty changes), and physics (energy and phase transitions)? The author gives a unified picture showing that generation is like carefully guiding noise so it “breaks ties” between different possible outcomes at just the right moments, turning randomness into structure.
What questions does the paper ask?
Here are the main questions the paper explores in everyday terms:
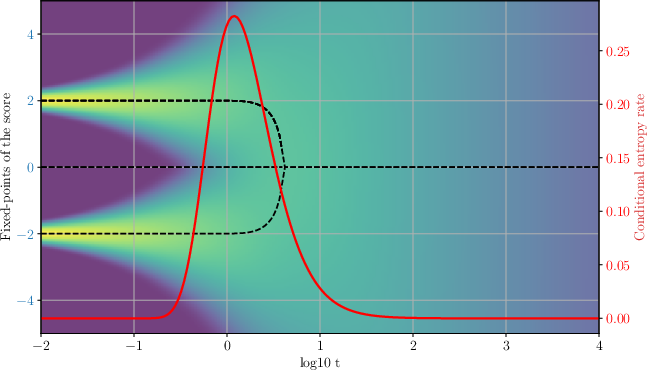
- How fast does a diffusion model reveal information about the final thing it’s making as it denoises? (This speed is called the “generative bandwidth.”)
- What controls that information speed during generation?
- Why do denoising paths sometimes “branch,” like a road that splits into two? What makes the model “decide” between possible outcomes?
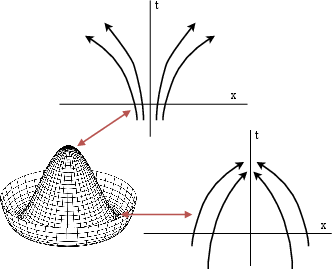
- How are these decisions connected to ideas from physics, like symmetry breaking and phase transitions (think water freezing or a ball choosing a side when balanced on a hill)?
- Can we measure all this using simple quantities that engineers and scientists can compute?
How do they paper it? (Methods and analogies)
The paper uses a few simple ideas and analogies to make the math intuitive:
- Twenty Questions analogy: Imagine playing “Twenty Questions.” Each answer reduces uncertainty about the hidden word. The paper treats generation the same way: at each time step, the model reduces uncertainty about the final sample. The rate of uncertainty reduction is the model’s “bandwidth.”
- Forward vs. reverse processes: In diffusion models, the forward process adds noise (like blurring a photo more and more). The reverse process removes noise, step by step, to recover a clean sample.
- The score function: During reverse diffusion, the model uses a learned function (called the “score”) that points in the best direction to remove noise. Think of it as an arrow field over space telling the model “move this way to look more like real data.”
- Divergence (arrows spreading in/out): The paper looks at whether these arrows tend to spread out or pull together on average. This “divergence” tells us whether nearby generative paths will split (branch) or merge.
- Fixed points and branching: A “fixed point” is a place where the score arrow becomes zero (no push). Tracking these fixed points over time shows when paths split into alternatives—a sign of the model facing a “choice” between possible outcomes.
- Symmetry breaking: At special moments (like balancing a pencil upright), tiny pushes from noise can make the system pick one of several symmetric options. The paper argues generation often works by carefully using noise to break such symmetries at the right times.
- Information geometry: The paper also connects the information flow to the Fisher information (a way to measure how sensitive a probability is to changes). This gives a geometric view of what directions in space carry meaningful data versus directions that are noise.
What did they find, and why is it important?
Below are the key findings, summarized in approachable terms:
- Information speed is controlled by “arrow spread”:
- The generative bandwidth (how fast uncertainty about the final sample drops) is directly tied to the expected divergence of the score’s arrows. When arrows tend to spread in certain directions, paths branch and information flows quickly; when arrows suppress spreading, information flows slowly.
- Peaks in information transfer line up with critical “decision moments,” where the model chooses between possible outcomes—just like answering a crucial question in Twenty Questions.
- The score is a smart noise filter:
- The score lets the model ignore noise that would push it off the data manifold (the “surface” where real data lives), and pay attention to noise that helps make genuine choices between plausible outputs. In short, it filters noise to keep only the useful bits.
- Branching equals symmetry breaking:
- When the model faces symmetric options (like two equally likely choices), tiny random pushes get amplified near special “critical points.” This is like a phase transition in physics. The paper shows these branching moments can be studied by looking at when the score’s stability changes (a sign of symmetry breaking).
- A clear link to information geometry:
- The rate at which uncertainty falls equals (up to a constant) the average of the Fisher information’s eigenvalues. That means directions that carry meaningful structure (on the data manifold) boost information flow, while off-manifold directions are suppressed.
- This also explains why the effective dimensionality of the data (how many meaningful directions exist) limits the maximum information speed.
- Thermodynamic view:
- The paper shows how total entropy (overall disorder) behaves consistently: even though “making decisions” during reverse diffusion looks like creating more uncertainty locally, the full accounting (including the forward process) never breaks the second law of thermodynamics.
Why does this matter? (Implications and impact)
This unified view has several practical and scientific benefits:
- Better training and sampling schedules: If we know when information transfer peaks (the critical moments), we can design time schedules that focus compute where it matters most, potentially making models faster and higher quality.
- Diagnosing problems: Branching analysis helps explain issues like memorization, mode collapse, and generalization. By studying the fixed points and their stability, we can tell whether a model is overly confident (too few branches) or too chaotic (too many unstable splits).
- Model design with physics in mind: Seeing generation as controlled symmetry breaking suggests new architectures that build in hierarchical “choices” (from coarse to fine detail), possibly aligning with how semantics emerge in images, text, and audio.
- Clearer theory of “how generation works”: Tying together dynamics (trajectories), information (entropy and Fisher information), and thermodynamics (entropy production) offers a common language for research across machine learning and physics.
In short, the paper argues that diffusion models work by carefully managing when and how noise drives decisions, turning randomness into meaningful structure. The score function is the traffic controller that filters noise, the branching points are the key choices, and the flow of information reveals where and when those choices happen.
Knowledge Gaps
Knowledge gaps, limitations, and open questions
Below is a concise list of concrete gaps and open questions that the paper leaves unresolved and that future research could address.
- Formalize the theory beyond the simplified forward SDE used (pure additive, isotropic Gaussian “heat” forward process). Extend derivations to variance-preserving/variance-exploding SDEs with drift, anisotropic diffusion, data-dependent noise, and discrete-time/jump processes.
- Quantify how discretization (finite-step solvers, predictor–corrector schemes, probability-flow ODE vs SDE samplers) alters conditional entropy production, divergence, and bifurcation phenomena; derive error bounds and stability conditions under practical integrators.
- Provide constructive, scalable estimators for the conditional entropy rate, expected divergence, and Jacobian/Lyapunov spectra in high dimensions (e.g., trace/Fisher information via Hutchinson estimators, JVP/VJP-based methods), including variance control and bias analysis.
- Empirically validate that peaks in conditional entropy production align with generative “decisions” (bifurcations) and semantic emergence on real image/audio/text models; devise protocols to detect critical times t_c in practice.
- Develop algorithms that adapt the time schedule to target high-information-transfer regions (entropic time change) during both training and sampling; characterize gains vs compute cost and robustness across datasets.
- Characterize how training imperfections (finite data, model misspecification, regularization, architecture, optimizer dynamics) distort the score field’s divergence and fixed-point structure, and how this impacts bandwidth and bifurcations.
- Analyze the impact of inference-time modifications (e.g., classifier-free guidance, guidance scale, conditioning strength) on entropy rate, divergence, and branching behavior; quantify the trade-off between guidance, mode coverage, and instability.
- Generalize the fixed-point and symmetry-breaking analysis from mixtures of delta distributions and orthogonality assumptions to continuous, curved data manifolds and realistic multimodal densities; provide non-asymptotic bounds.
- Define operational order parameters and practical diagnostics for detecting spontaneous symmetry breaking in learned models (e.g., spectral signatures of the Jacobian, local Lyapunov exponents, Fisher eigen-structure) with actionable thresholds.
- Bridge the information-geometric results to non-Gaussian forward processes and to common parameterizations used in practice (epsilon-, v-, and x0-prediction); clarify when Fisher-trace identities and entropy-rate formulas still hold exactly or approximately.
- Reconcile the “maximum generative bandwidth” scaling with dimensionality D with practical constraints (step counts, compute budgets, discretization error, numerical stability); propose normalized, comparable bandwidth metrics (e.g., bits/dimension/time).
- Provide a rigorous stochastic-thermodynamic treatment of reverse-time entropy production (housekeeping vs excess entropy, time-inhomogeneous driving, Itô vs Stratonovich interpretations) and clarify the “paradoxical” entropy term in reverse dynamics.
- Study robustness of the theory under approximate scores that are not exact gradients of any log-density (non-conservative vector fields from learning error); determine how non-integrability affects fixed-points, divergence, and the phase-transition picture.
- Quantify the relationship between manifold dimension and entropy production empirically on real models; validate whether reductions in the Fisher metric’s spectrum correspond to observed bandwidth suppression and denoising difficulty.
- Develop methods to map and summarize the global “decision tree” of fixed-points/attractors for high-dimensional models (e.g., path following, continuation methods, homotopy), and relate nodes/branches to data modes and semantics.
- Establish conditions under which memorization, spurious states, or mode collapse manifest as phase transitions in the learned score field; derive tests and preventative training/sampling strategies based on stability analysis.
- Analyze how noise schedules and parameterizations shape the timing and sharpness of bifurcations; optimize schedules for stability and sample quality while preserving desired information transfer.
- Extend the framework to conditional models p(x|c): decompose information flow between noise and conditioning (e.g., via partial information decomposition), and paper how conditioning reshapes divergence and bifurcations.
- Specify how to estimate and use local Lyapunov spectra during sampling (on-the-fly Jacobian-vector products) to detect and manage unstable regions (e.g., adaptive step sizes, regularization of the vector field).
- Provide benchmarks and visualizations linking entropy rate peaks to interpretable generative events (e.g., coarse-to-fine semantic emergence), including ablations across architectures, datasets, and samplers.
- Integrate connections to stochastic localization and functional inequalities (e.g., log-Sobolev, Bakry–Émery) to derive general bounds on entropy production and mixing that apply to state-of-the-art diffusion setups.
- Examine data with heavy tails, bounded support, or strong anisotropy to test whether divergence/entropy predictions match observed dynamics and whether the phase-transition picture persists.
- Clarify how architecture choices (U-Nets, attention, normalization, skip connections) constrain the learned score’s Jacobian spectrum and thus the attainable bandwidth and stability.
- Investigate deterministic probability-flow ODE sampling where pathwise entropy does not increase; reconcile the “decision-making via noise” narrative with deterministic flows and characterize when branching is still meaningful.
- Propose practical tooling to measure/visualize the Fisher metric’s eigenstructure along typical trajectories and relate it to local manifold geometry and denoising uncertainty throughout sampling.
Collections
Sign up for free to add this paper to one or more collections.