Spacetime Geometry of Denoising in Diffusion Models (2505.17517v1)

Abstract: We present a novel perspective on diffusion models using the framework of information geometry. We show that the set of noisy samples, taken across all noise levels simultaneously, forms a statistical manifold -- a family of denoising probability distributions. Interpreting the noise level as a temporal parameter, we refer to this manifold as spacetime. This manifold naturally carries a Fisher-Rao metric, which defines geodesics -- shortest paths between noisy points. Notably, this family of distributions is exponential, enabling efficient geodesic computation even in high-dimensional settings without retraining or fine-tuning. We demonstrate the practical value of this geometric viewpoint in transition path sampling, where spacetime geodesics define smooth sequences of Boltzmann distributions, enabling the generation of continuous trajectories between low-energy metastable states. Code is available at: https://github.com/Aalto-QuML/diffusion-spacetime-geometry.

• The paper introduces an information geometric framework that treats denoising in diffusion models as geodesic paths on a spacetime statistical manifold using a Fisher-Rao metric.
• The method leverages the exponential family structure of denoising distributions to simplify geodesic computation and enable efficient transition path sampling.
• Experimental results show that the computed geodesics yield smoother trajectories, reduced semantic changes, and lower variance in both image and molecular transition interpolations.

Spacetime Geometry of Denoising in Diffusion Models

This paper introduces an information geometric perspective on diffusion models, framing the denoising process within a statistical manifold. By considering noisy samples across various noise levels as a spacetime manifold, the authors derive a Fisher-Rao metric that defines geodesics representing shortest paths between noisy points. The authors demonstrate that this manifold is an exponential family, which enables efficient geodesic computation, and showcase its application in transition path sampling for generating continuous trajectories between low-energy metastable states.

Statistical Manifold and Fisher-Rao Metric

The core concept is to treat the latent space of diffusion models as a $(D+1)$-dimensional statistical manifold, where $D$ is the data dimensionality and the additional dimension represents the noise level $t$. This manifold consists of denoising distributions $p(_0|)$, where $_t$ is a noisy sample at noise level $t$ and $_0$ is the clean data. The Fisher-Rao metric is then applied to characterize the geometry of this denoising process. This approach contrasts with typical methods that rely on the pullback metric of the decoder, which the authors argue is computationally expensive due to the deterministic nature of the decoder defined by an ODE. The Fisher-Rao metric $\mathcal{I}_$ is defined as:

$$\mathcal{I}_ = \mathbb{E}_{ \sim p( | )}\Big[\nabla_{}\log p( | )\nabla_{}\log p( | )^{\top}\Big]$$

which quantifies how small changes in the parameters $affect the probability distribution$p(\cdot | )$. ## Exponential Family and Geodesic Computation A key contribution is the demonstration that the denoising distributions $p(_0|_t)$$form an exponential family. This insight significantly simplifies the computation of geodesics on the spacetime manifold. The authors derive closed-form expressions for both the natural parameter$$()$and the expectation parameter$()$$of this exponential family. The natural parameter is:$$(, t)=\left( \frac{\alpha_t}{\sigma_t^2} , -\frac{\alpha_t^2}{2\sigma_t^2} \right)$and the expectation parameter is:$(, t) = \bigg( \underbrace{\frac{1}{\alpha_t}\Big( + \sigma_t^2 \nabla_ \log p_t()\Big)}{E\big[_0 | \big]}, \underbrace{\frac{\sigma_t^2}{\alpha_t} _ E[_0 | ] + \big|E[_0 | ]\big|^2}{E\big[ | 0 |^2 \,\mid\, \big]} \bigg)$$The Fisher-Rao metric for exponential families simplifies to:$$ \mathcal{I} = \left(\frac{\partial ()}{\partial }\right)^{\top} \left( \frac{\partial ()}{\partial } \right) $$ and not on the base measure or log-partition function, which are typically hard to estimate.

Transition Path Sampling

Figure 1: Spacetime geodesics between clean images remove less information than interpolation through full noise.

The authors demonstrate the practical utility of their framework in transition path sampling (TPS). In TPS, the goal is to find probable transition paths between low-energy states, often in molecular dynamics simulations. By assuming a Boltzmann distribution for the data, the denoising distribution also follows a tractable energy function. The spacetime geodesics then define smooth sequences of Boltzmann distributions, enabling the generation of continuous trajectories between metastable states. The authors employ annealed Langevin dynamics to sample transition paths along the computed geodesics.

Figure 2: PF-ODE paths are similar to energy-minimizing geodesics.

Constrained Path Sampling

The paper also explores constrained path sampling, where additional constraints are imposed on the geodesic interpolants. This is formulated as a constrained optimization problem, where a penalty function is added to the energy functional. The authors demonstrate two examples: (i) penalizing transition path variance by favoring high SNR regions, and (ii) avoiding restricted regions in the data space by penalizing paths that enter those regions using a KL divergence-based penalty.

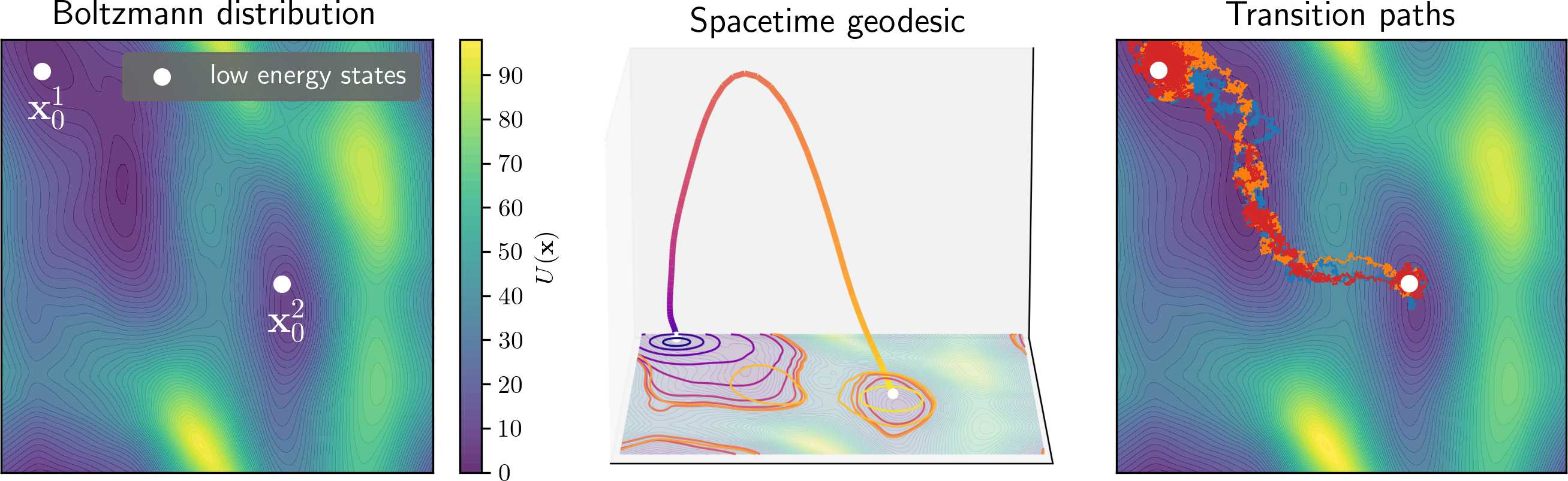
Figure 3: Spacetime geodesics enable sampling transition paths between low-energy states.

Experimental Results

The authors present several experimental results to validate their framework. They compare trajectories obtained by solving the PF-ODE with geodesics between the same endpoints, observing that geodesics exhibit less curvature than PF-ODE trajectories in early sampling stages. They also perform image interpolations, demonstrating that spacetime geodesics introduce fewer semantic changes compared to standard interpolation techniques. Furthermore, they apply their framework to molecular configuration transitions, showcasing its ability to generate transition paths between different states of Alanine Dipeptide.

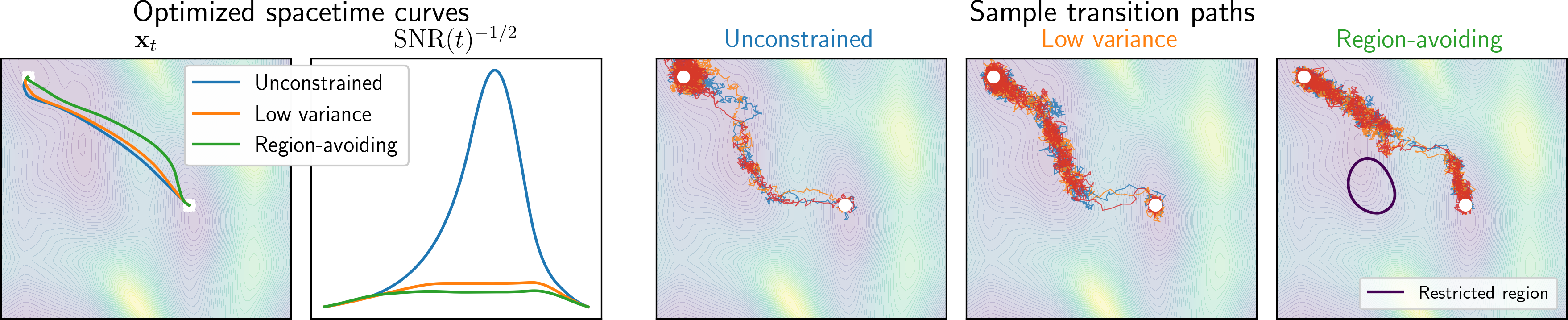
Figure 4: Vanilla transition paths can be constrained to have lower variance, or successfully avoid a restricted region $p(\cdot | ^*)$.

Limitations and Future Directions

The paper acknowledges limitations, particularly the numerical instability of optimizing geodesics between nearly clean samples due to the denoising distribution approaching a Dirac delta. Future research directions include exploring the use of the framework to improve sampling strategies and addressing the limitations related to low-noise samples.

Figure 5: Spacetime geodesic decodes to less realistic images, but introduces less semantic changes than standard interpolations.

Conclusion

This paper offers a novel perspective on diffusion models by introducing the concept of a spacetime statistical manifold. By leveraging the exponential family property of denoising distributions, the authors enable tractable geodesic computation and demonstrate its application in transition path sampling. This work deepens the understanding of the latent space in diffusion models and paves the way for future research in enhanced sampling techniques and other applications of the spacetime geometric framework.