TabPFN: One Model to Rule Them All? (2505.20003v1)

Abstract: Hollmann et al. (Nature 637 (2025) 319-326) recently introduced TabPFN, a transformer-based deep learning model for regression and classification on tabular data, which they claim "outperforms all previous methods on datasets with up to 10,000 samples by a wide margin, using substantially less training time." Furthermore, they have called TabPFN a "foundation model" for tabular data, as it can support "data generation, density estimation, learning reusable embeddings and fine-tuning". If these statements are well-supported, TabPFN may have the potential to supersede existing modeling approaches on a wide range of statistical tasks, mirroring a similar revolution in other areas of artificial intelligence that began with the advent of LLMs. In this paper, we provide a tailored explanation of how TabPFN works for a statistics audience, by emphasizing its interpretation as approximate Bayesian inference. We also provide more evidence of TabPFN's "foundation model" capabilities: We show that an out-of-the-box application of TabPFN vastly outperforms specialized state-of-the-art methods for semi-supervised parameter estimation, prediction under covariate shift, and heterogeneous treatment effect estimation. We further show that TabPFN can outperform LASSO at sparse regression and can break a robustness-efficiency trade-off in classification. All experiments can be reproduced using the code provided at https://github.com/qinglong-tian/tabpfn_study (https://github.com/qinglong-tian/tabpfn_study).

• The paper introduces TabPFN, a transformer-based model that uses in-context Bayesian inference for tabular data analysis.
• It demonstrates superior performance in regression, classification, semi-supervised learning, and covariate shift adaptation.
• Experiments reveal TabPFN's robustness in treatment effect estimation and noise resilience, positioning it as a scalable foundation model.

Detailed Analysis of "TabPFN: One Model to Rule Them All?"

The paper "TabPFN: One Model to Rule Them All?" introduces a transformer-based deep learning model, TabPFN, designed specifically for regression and classification tasks on tabular data. The authors claim that TabPFN outperforms existing methods, such as random forests and boosting models, on datasets with up to 10,000 samples, while requiring significantly less training time. This model is presented as a "foundation model" for tabular data, capable of supporting diverse tasks like data generation, density estimation, and learning reusable embeddings.

TabPFN Model Architecture and Training

TabPFN adopts a transformer architecture to approximate posterior predictive distributions (PPDs), leveraging the paradigm of in-context learning (ICL). The model is pre-trained on synthetic datasets derived from structural causal models (SCMs), allowing it to perform approximate Bayesian inference.

Transformer-based Architecture

By using transformers, TabPFN benefits from the architecture's ability to model complex dependencies within data. Transformers, initially successful in natural language processing, are capable of capturing intricate relationships within tabular datasets. This allows the model to generalize well across different types of statistical tasks.

In-context Learning and Bayesian Inference

In-context learning within TabPFN is treated as Bayesian inference, where the model learns a mapping from datasets to posterior distributions. The large parameter space of the transformer ($\approx$ 7M parameters) enables it to model complex priors defined within the SCM framework. This approach provides computational efficiency, as computations can be amortized, reducing the need for extensive re-training when new data is presented.

Experimental Validation

The paper validates TabPFN through various experimental setups, demonstrating its effectiveness in semi-supervised learning, heterogeneous treatment effect estimation, and adaptation under covariate shift.

Semi-supervised Learning

In the semi-supervised setting, TabPFN is shown to outperform state-of-the-art methods in parameter estimation by leveraging unlabeled data efficiently (Figure 1).

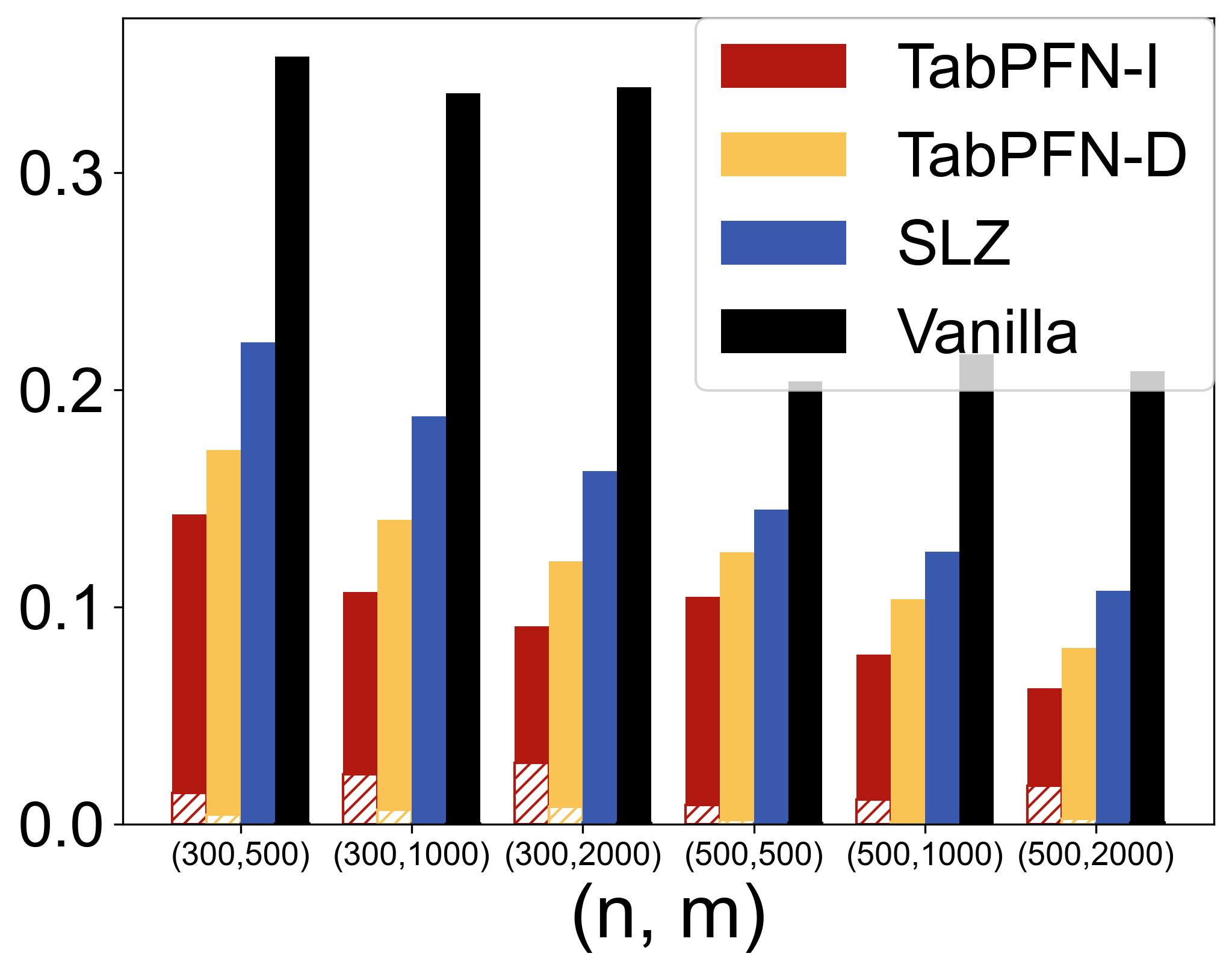
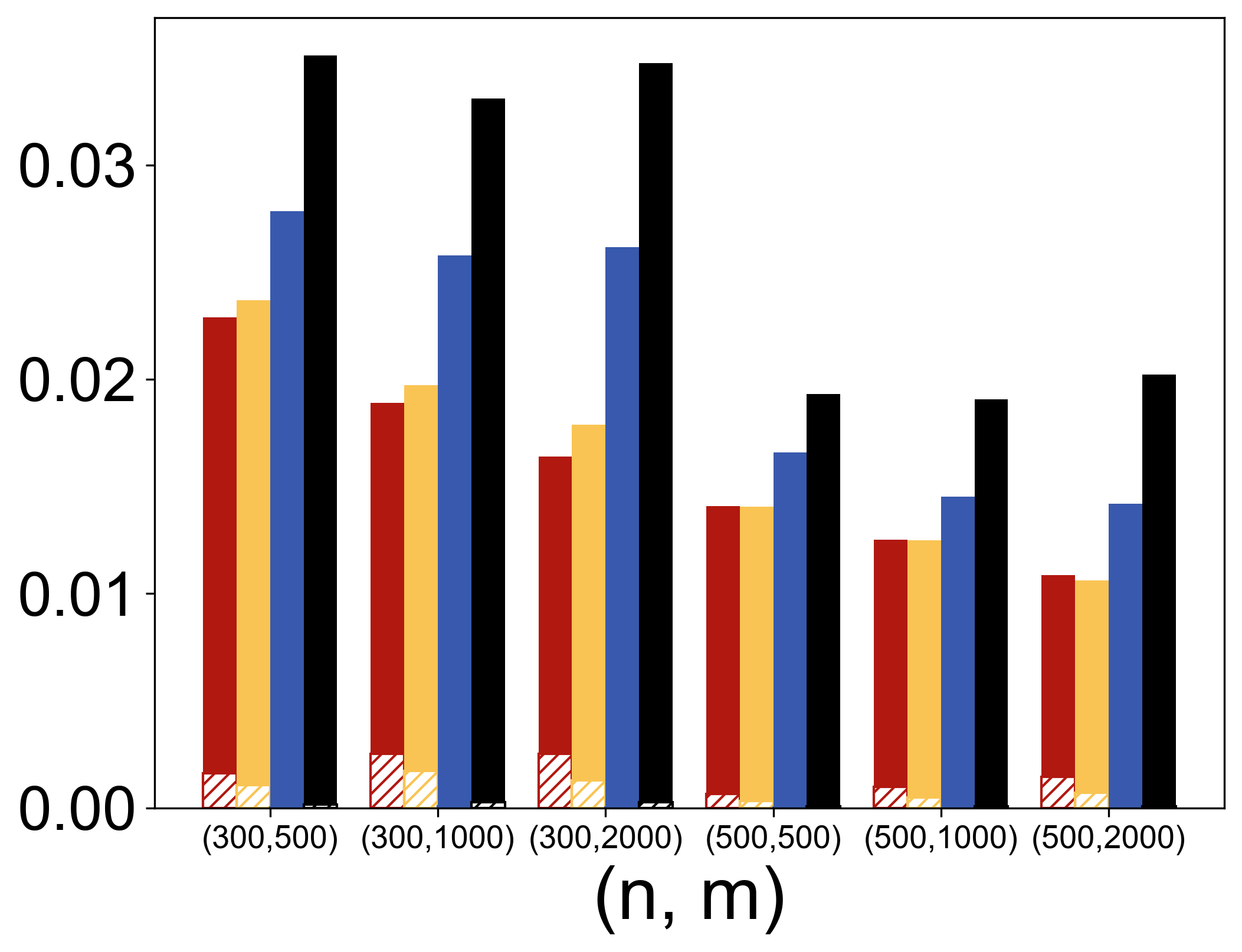
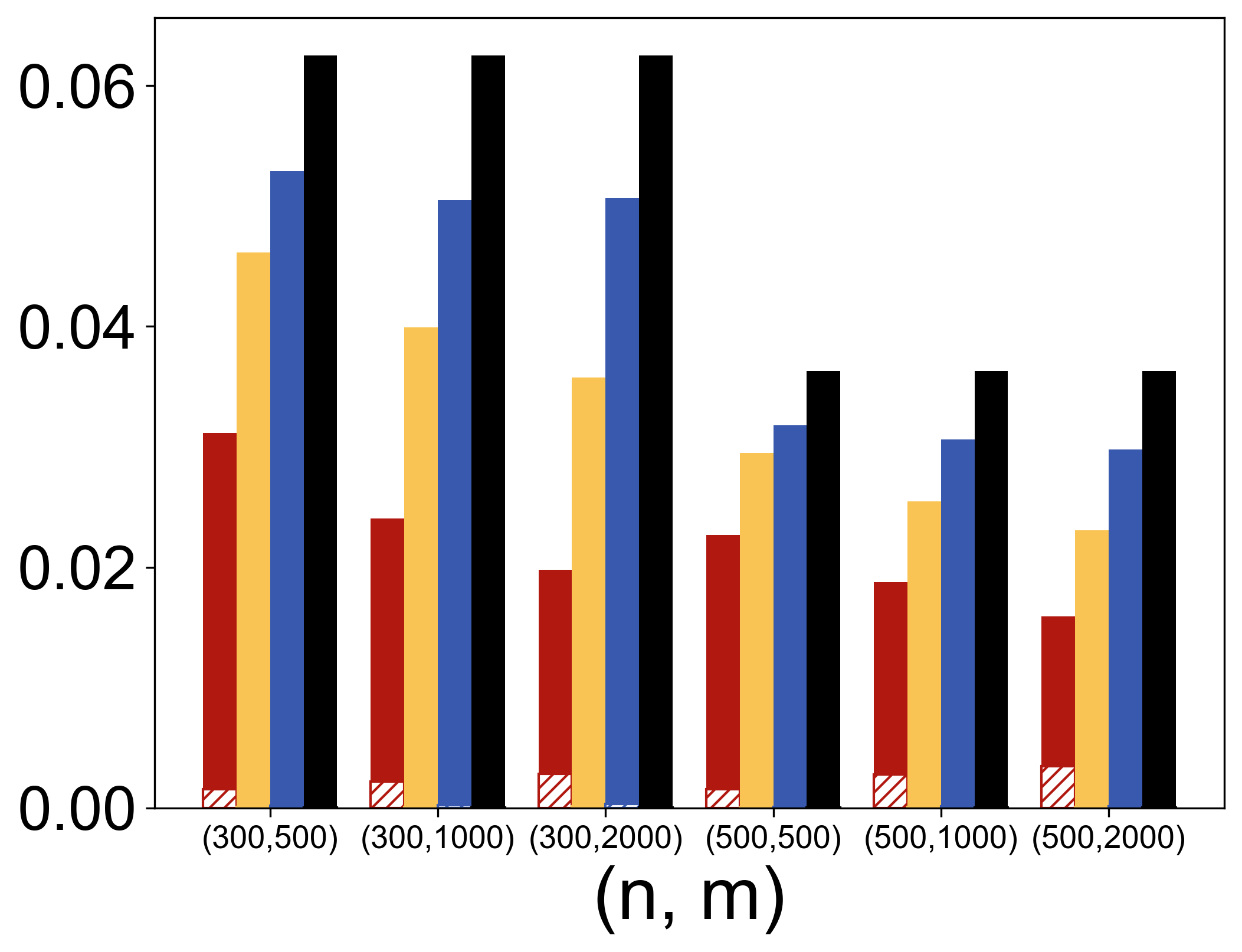
Figure 1: MSE results for linear (top left), logistic (top right), and quantile ($\tau=0.25$, bottom left) regressions when $p=5$. MSE results for logistic regression with various $p$ (bottom right) when $(n,m)=(300,500)$.

Heterogeneous Treatment Effect Estimation

TabPFN significantly improves estimation accuracy for conditional average treatment effects (CATE) compared to existing meta-learner frameworks, especially under scenarios with complex confounding and large variability in treatment effects (Figure 2).

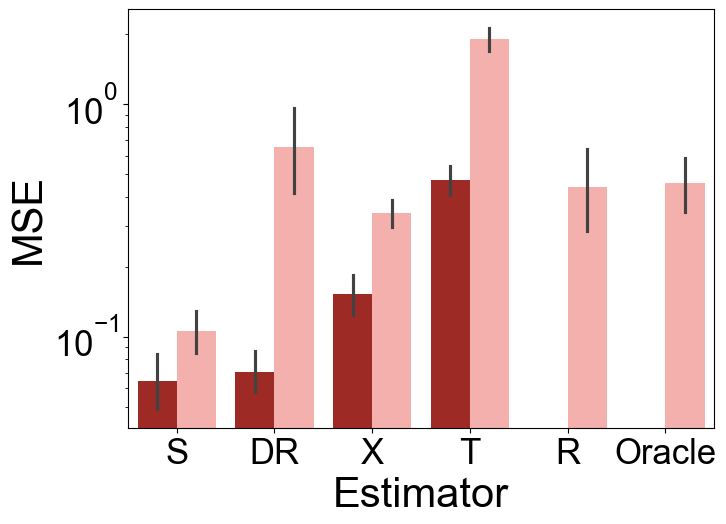
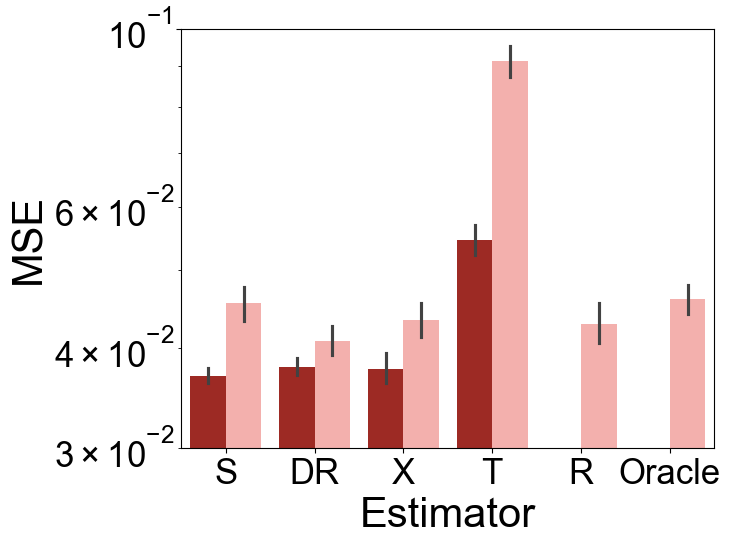
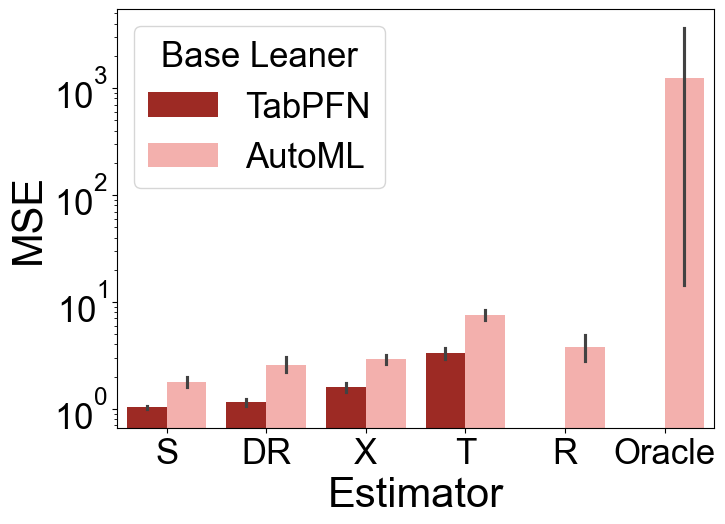
Figure 2: Test MSE of various CATE estimators under Setup A (top) and Setup E (bottom) over 100 repetitions. The left panels show results for the small-sample, high-variance scenario ($n = 500, \sigma^2 = 2$), while the right panels display the large-sample, low-variance scenario ($n = 2000, \sigma^2 = 0.5$).

Covariate Shift Adaptation

In contexts where the distribution of covariates shifts between training and testing datasets, TabPFN's performance in maintaining prediction accuracy surpasses that of pseudo-labeling and other established methods (Figure 3).

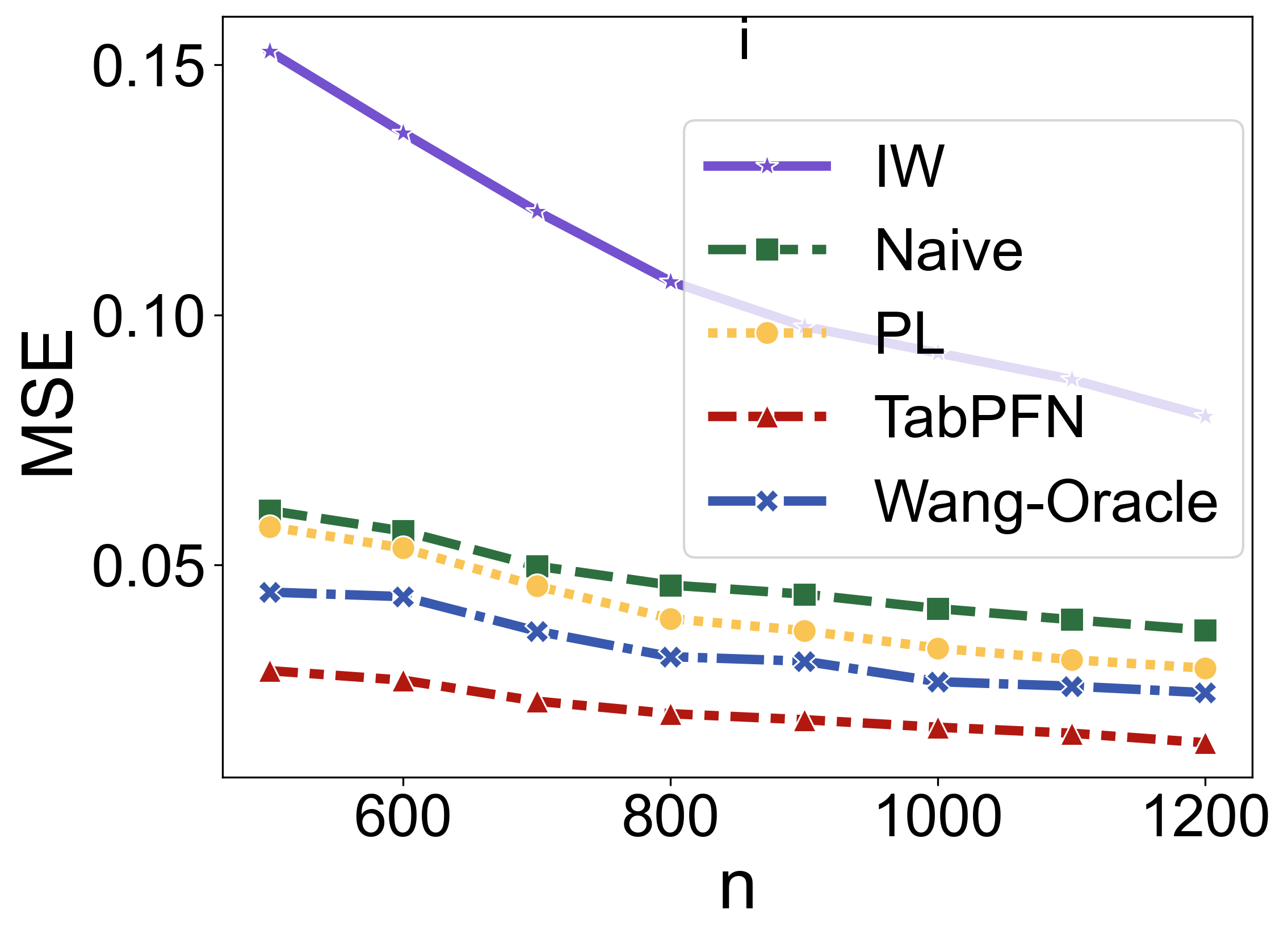
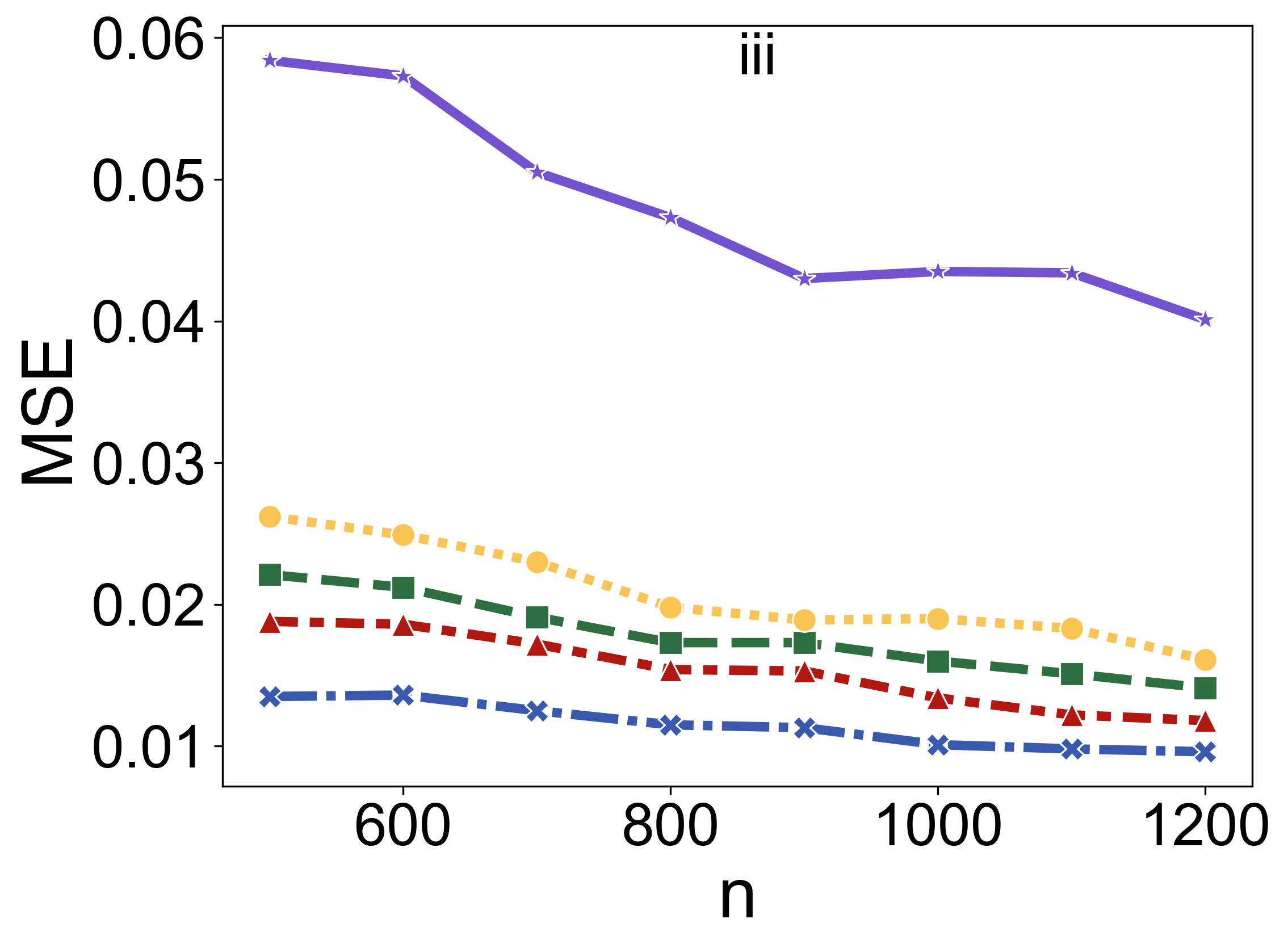
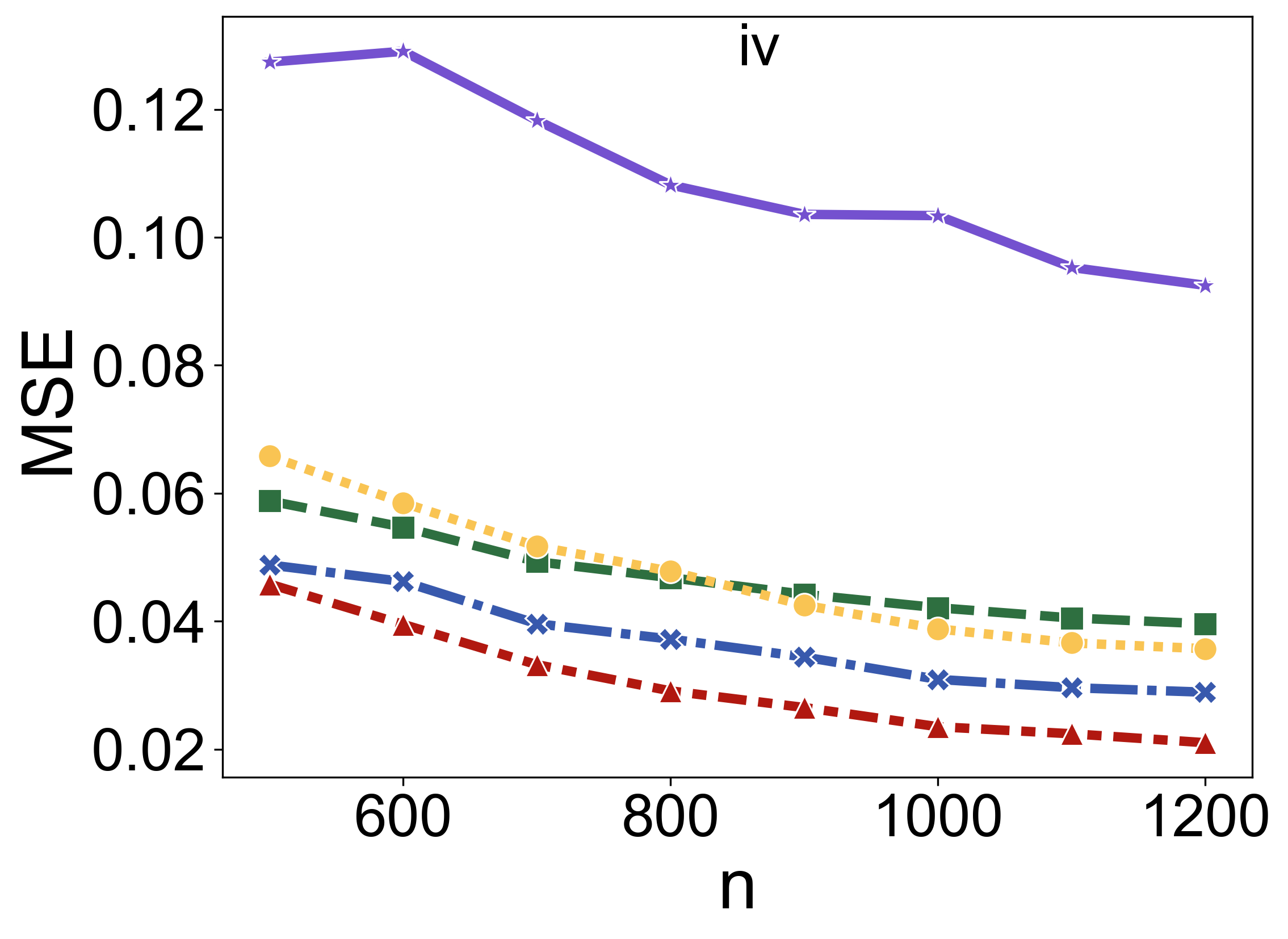
Figure 3: Comparison of prediction MSE for different covariate shift methods across varying sample sizes ($n$) and scenarios.

Inductive Biases and Robustness

The paper also explores the inductive biases of TabPFN through experiments in interpolation and extrapolation. The findings highlight TabPFN's flexibility in adapting to different functional forms and its robustness against label noise in classification tasks.

Interpolation and Extrapolation

TabPFN outperforms Gaussian Process Regression in interpolating and extrapolating various synthetic 1D and 2D functions, displaying unique responses to abrupt changes and data discontinuities (Figure 4).

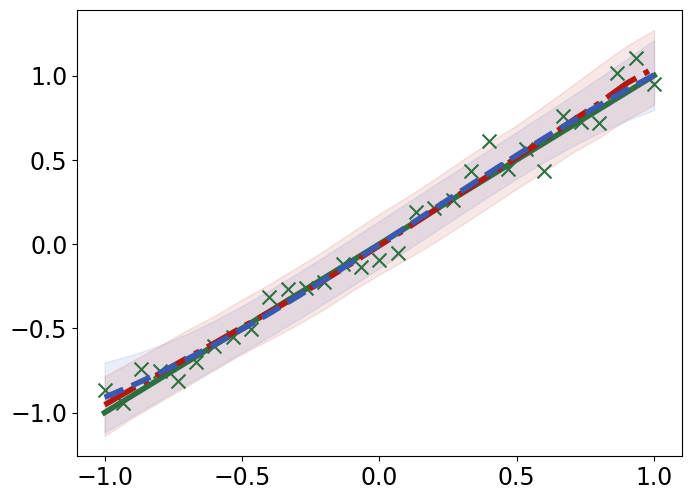
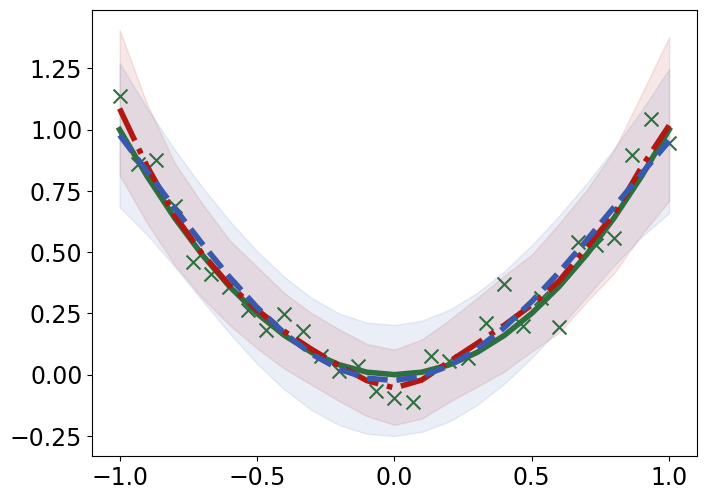
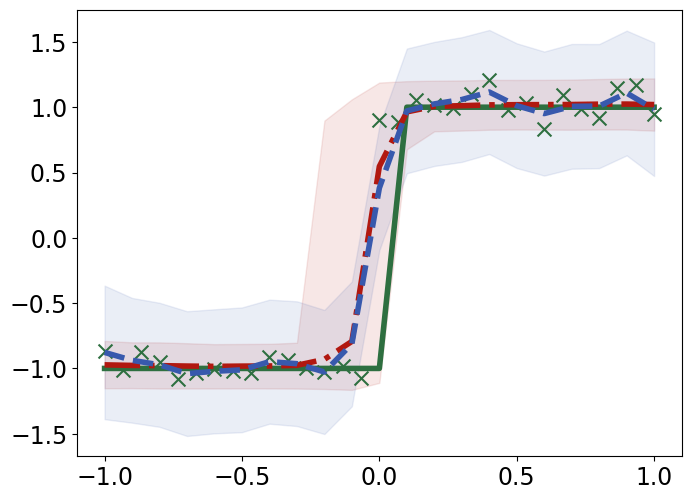
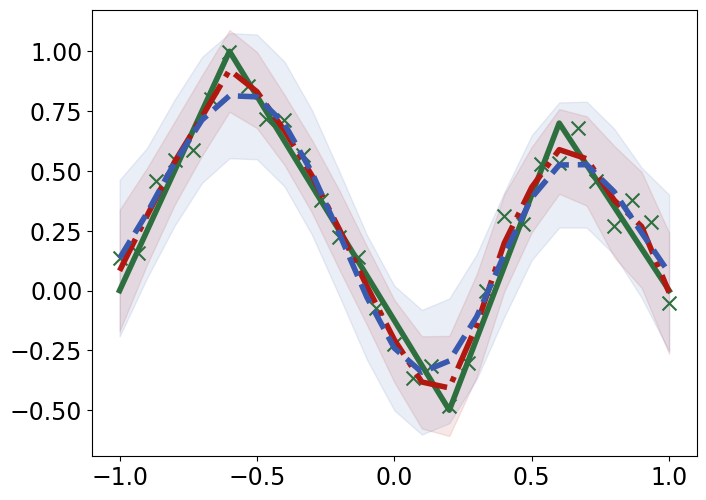
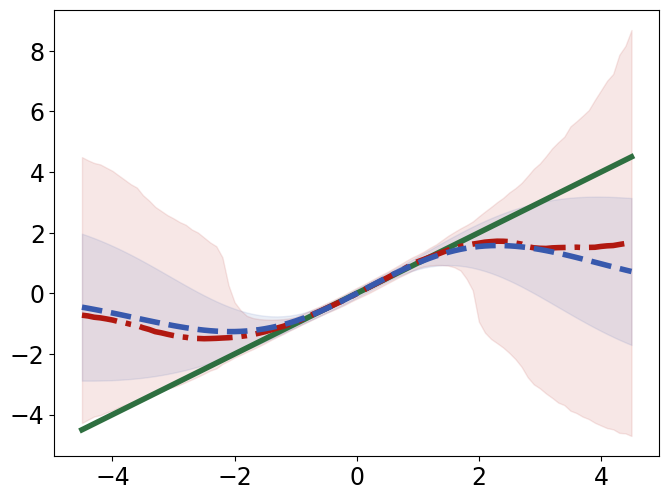
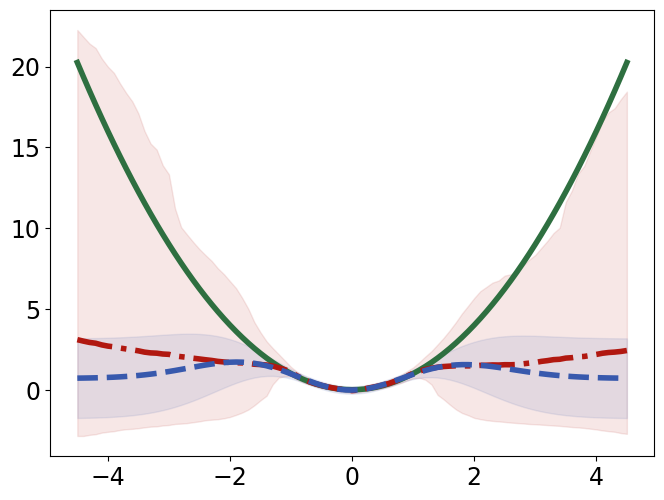
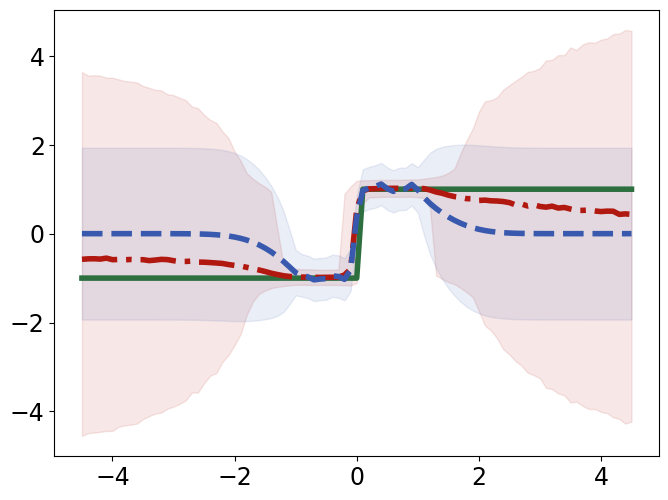
Figure 4: Interpolation (top) and extrapolation (bottom) performance of TabPFN (red) and Gaussian process regression (GPR; blue) regression on synthetic 1D functions, compared to ground truth (green).

Robustness to Noise

In classification tasks, TabPFN exhibits robustness to label noise, matching or surpassing the performance of linear and kernel-based methods across different noise levels and sample sizes (Figure 5).

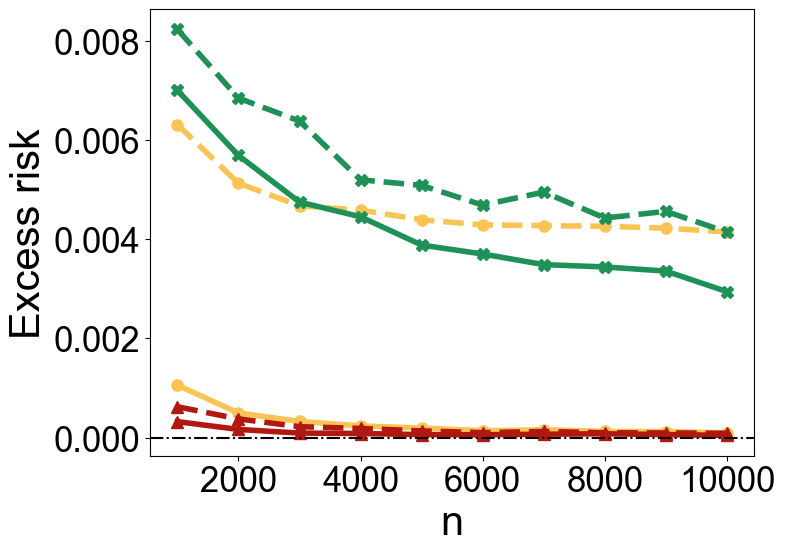
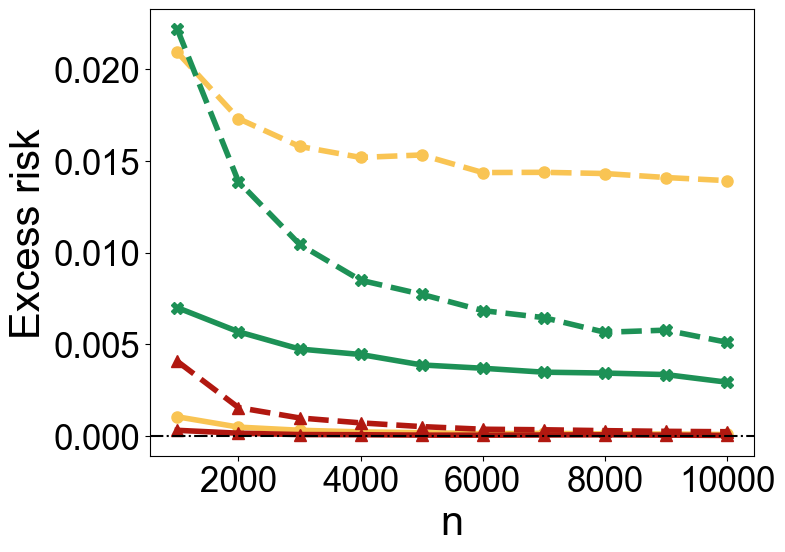
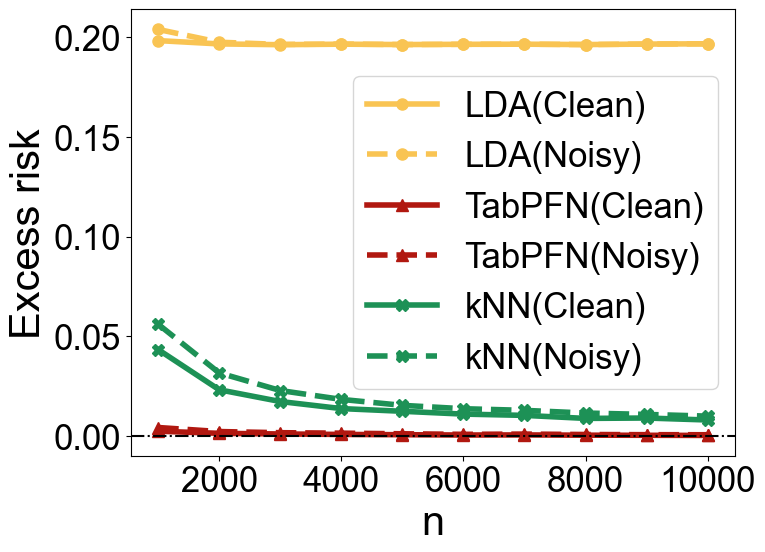
Figure 5: Excess risks under Model M1 (top row) and Model M2 (bottom row). The left column shows results for $\rho=0.1$, while the right column presents results for $\rho=0.3$.

Conclusion

TabPFN represents a significant advancement in modeling tabular data with transformers, providing a versatile tool capable of outperforming existing specialized models across various statistical tasks. As a potential foundation model for tabular data, TabPFN holds promise for future developments in automating statistical analysis and providing robust, scalable solutions for complex real-world datasets. Further exploration of its theoretical properties and scalability to higher-dimensional data could broaden its applicability and impact.