MoLAE: Mixture of Latent Experts for Parameter-Efficient Language Models (2503.23100v2)

Abstract: Mixture of Experts (MoE) has become a key architectural paradigm for efficiently scaling LLMs by selectively activating a subset of parameters for each input token. However, standard MoE architectures face significant challenges, including high memory consumption and communication overhead during distributed training. In this paper, we introduce Mixture of Latent Experts (MoLAE), a novel parameterization that addresses these limitations by reformulating expert operations through a shared projection into a lower-dimensional latent space, followed by expert-specific transformations. This factorized approach substantially reduces parameter count and computational requirements, particularly in existing LLMs where hidden dimensions significantly exceed MoE intermediate dimensions. We provide a rigorous mathematical framework for transforming pre-trained MoE models into MoLAE architecture, characterizing conditions for optimal factorization, and developing a systematic two-step algorithm for this conversion. Our comprehensive theoretical analysis demonstrates that MoLAE significantly improves efficiency across multiple dimensions while preserving model capabilities. Experimental results confirm that MoLAE achieves comparable performance to standard MoE with substantially reduced resource requirements.

• The paper introduces MoLAE, which decomposes expert operations into shared latent projections and expert-specific transformations to reduce parameters.
• It applies low-rank matrix factorization and SVD techniques to efficiently transform traditional MoE models into parameter-efficient MoLE systems.
• Experimental results on benchmarks like MMLU and GSM8K demonstrate that MoLAE maintains competitive performance with significantly lower memory and compute requirements.

MoLAE: Mixture of Latent Experts for Parameter-Efficient LLMs

Introduction

The necessity for scaling LLMs has led to the development of architectural paradigms like the Mixture of Experts (MoE), which efficiently scale model capacity without a proportional increase in computational overhead by activating only latent subsets of parameters. However, MoE architectures are often plagued by memory and communication bottlenecks due primarily to the redundant and extensive nature of expert modules.

The paper introduces the concept of Mixture of Latent Experts (MoLE), a methodology designed to overcome these challenges by mapping experts into a shared latent space. Each expert operation is decomposed into two components: a shared projection into a latent space and expert-specific transformations, significantly reducing the parameter count and computational demand. Additionally, the paper establishes a transformation framework for modeling pre-trained MoE architectures into MoLE systems, facilitating computational efficiency while preserving model performance.

Architectural Foundations

Traditional MoE Limitations

Standard MoE models face substantial inefficiencies due to memory consumption and communication overhead caused by the proliferation of expert modules. Specifically, the storage and synchronisation of parameters across numerous experts in feed-forward network layers induce significant practical challenges. On analyzing structures such as the Qwen1.5-MoE-A2.7B, a considerable amount of the parameters within the FFN layers is deemed redundant, capable of being approximated via lower-dimensional representations.

Conceptualizing MoLE

MoLE addresses these inefficiencies by reformulating experts' operations through a two-phase mechanism: (1) shared low-dimensional latent space projection and (2) expert-specific lower-complexity transformations. This dual operation enhances parameter efficiency, particularly at higher hidden dimensions, $n$, and reduced MoE intermediate dimensions, $m$.

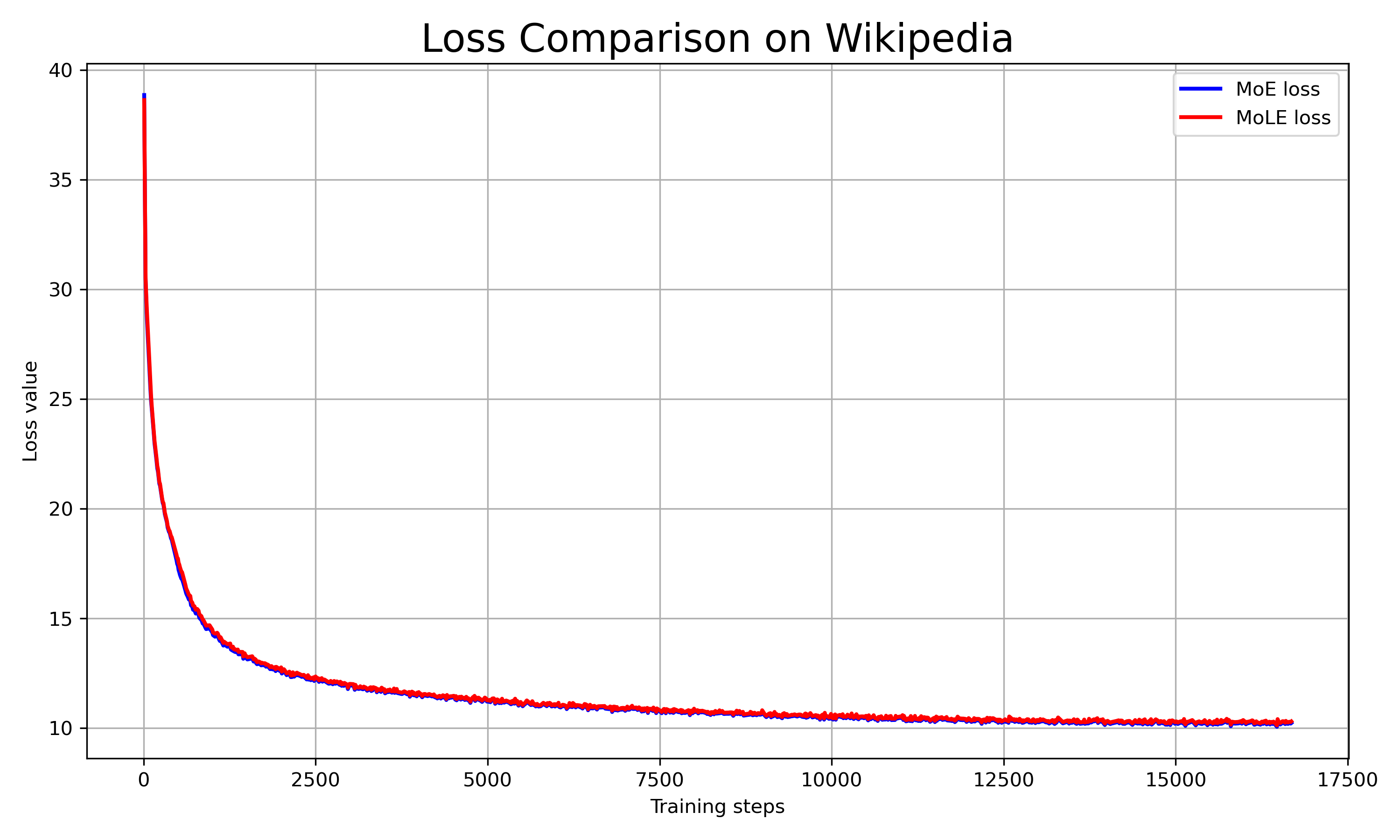
Figure 1: Comparison between MoE and MoLE shows slight differences in convergence patterns, with MoLE slightly higher in loss yet greatly reduced in parameters.

Detailed Implementation

Theoretical Framework

Transforming MoE to a MoLE architecture requires optimal factorization conditions. Given standard SVD techniques, each expert's weight matrix can be decomposed into low-dimensional matrix products that reflect shared and unique expert transformations. The framework optimizes these transformations to minimize approximation residuals, ensuring negligible performance drop while achieving memory efficiency.

Transformation Algorithm

Algorithmically, transforming MoE to MoLE involves the following steps:

1. Rank Reduction: Low-rank approximation of the original expert matrices.
2. Matrix Factorization: Using SVD on concatenated matrices to identify latent shared projections and expert-specific transformations.

This systematic transformation not only alleviates memory and compute burdens but also enhances cache efficiency, which is critical in reduced batch-size NLP tasks.

Experimental Results

Extensive empirical evaluation substantiates that MoLE achieves parity in performance with unfactored MoE models:

• Training loss trajectories on datasets such as English Wikipedia reveal that MoLE's parameter efficiency translates to competitive convergence, even at a reduced parameter footprint.
• Performance across MMLU, GSM8K, and Wikitext-2 benchmarks demonstrates MoLE's robust capability in resource-constrained environments.

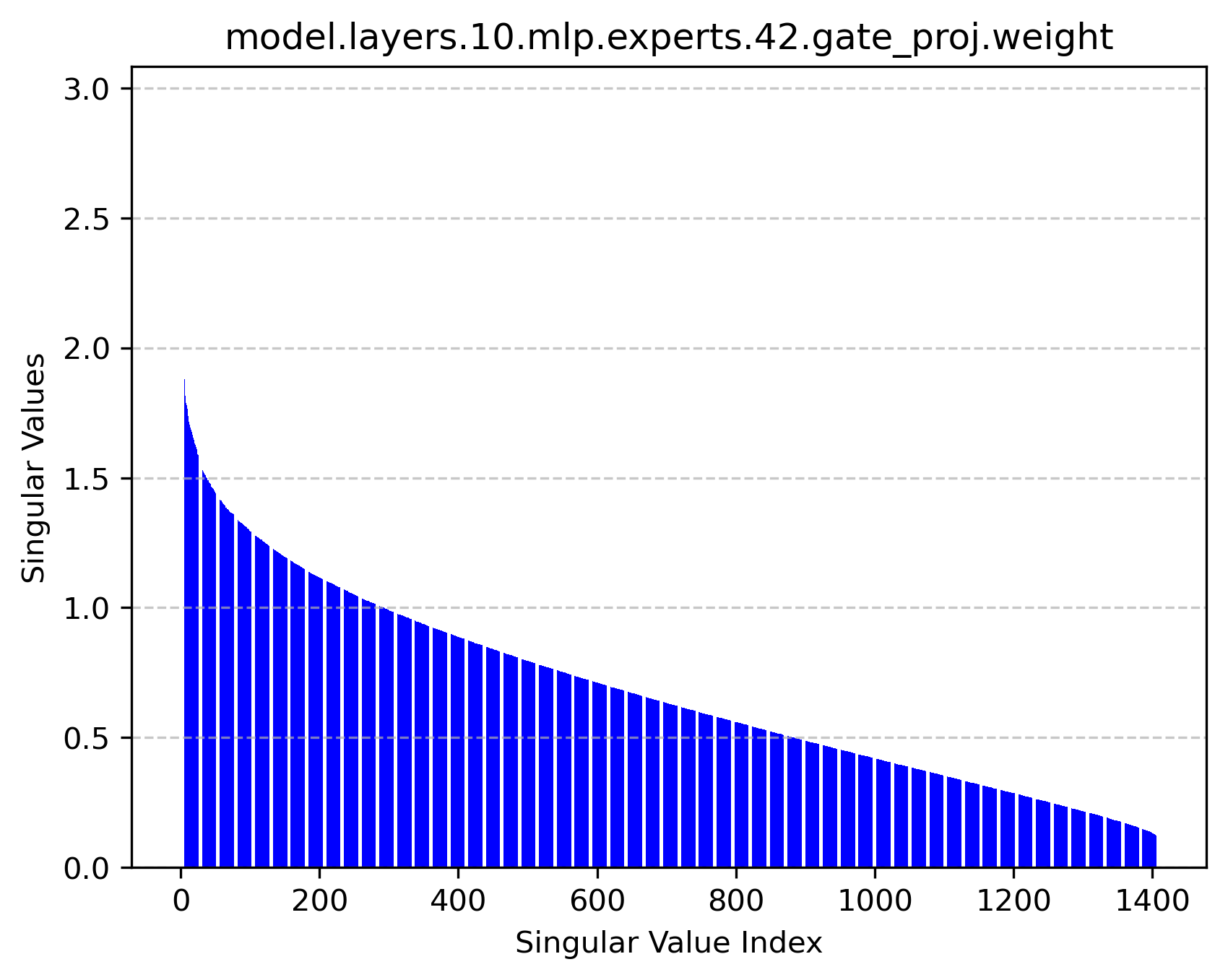
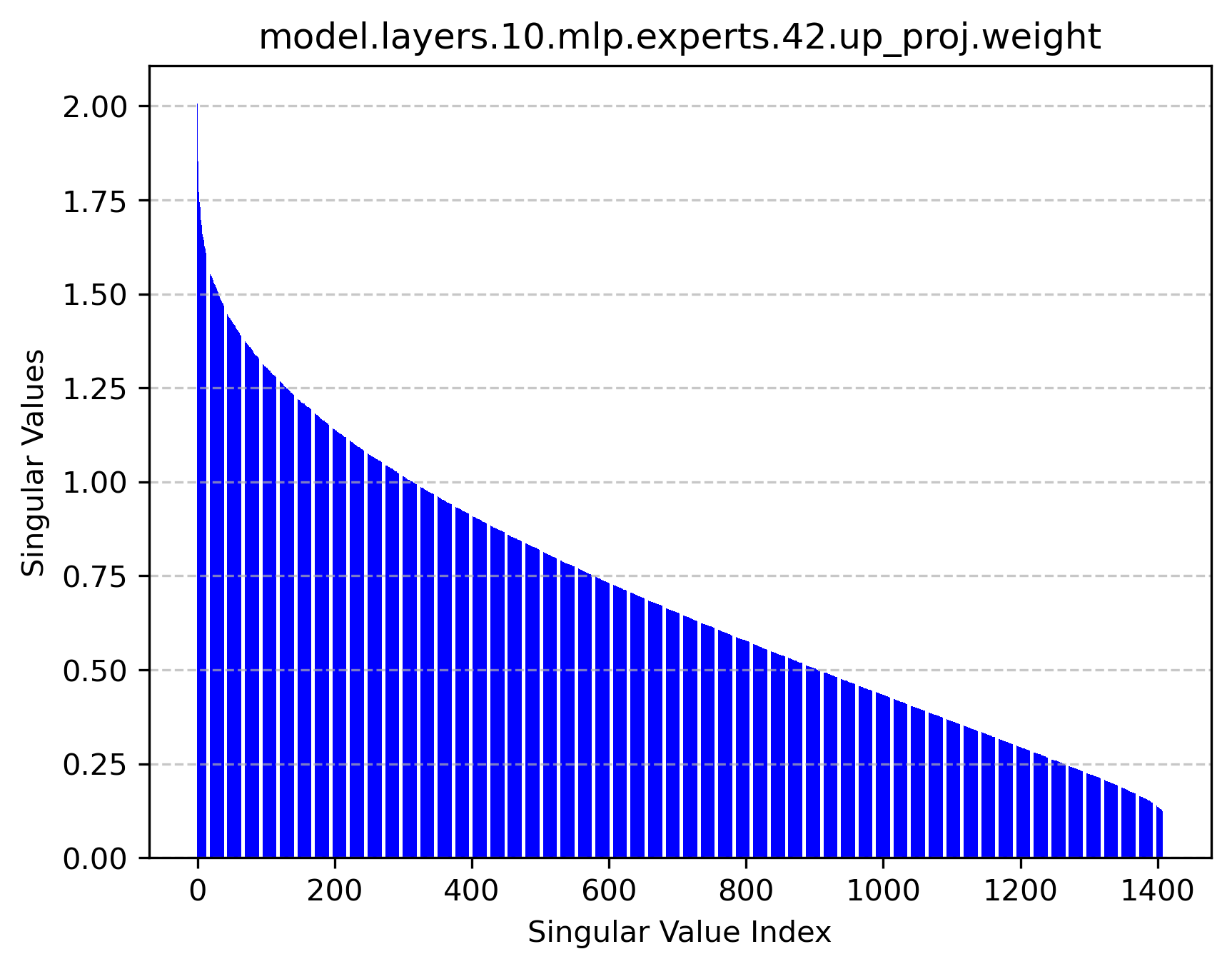
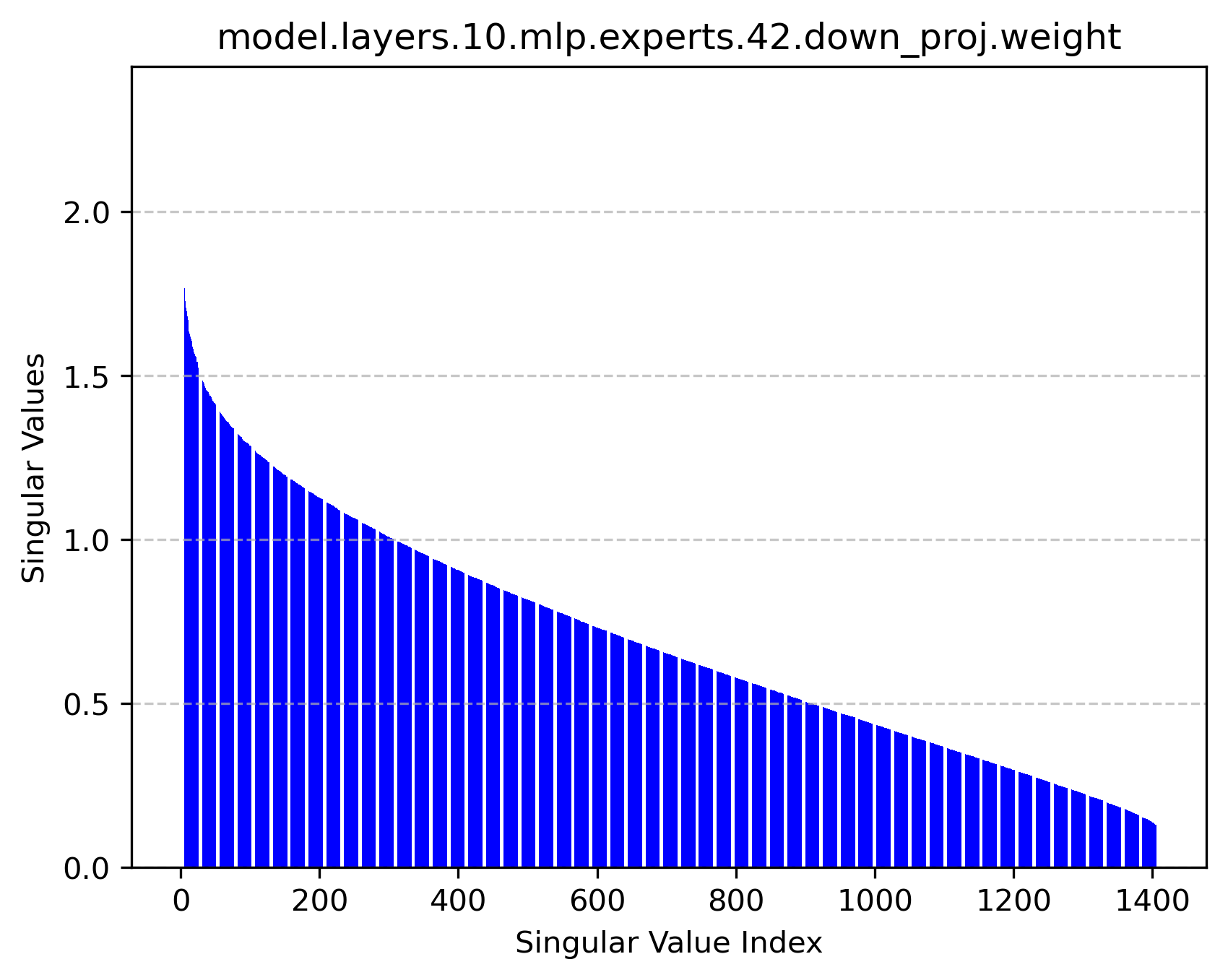
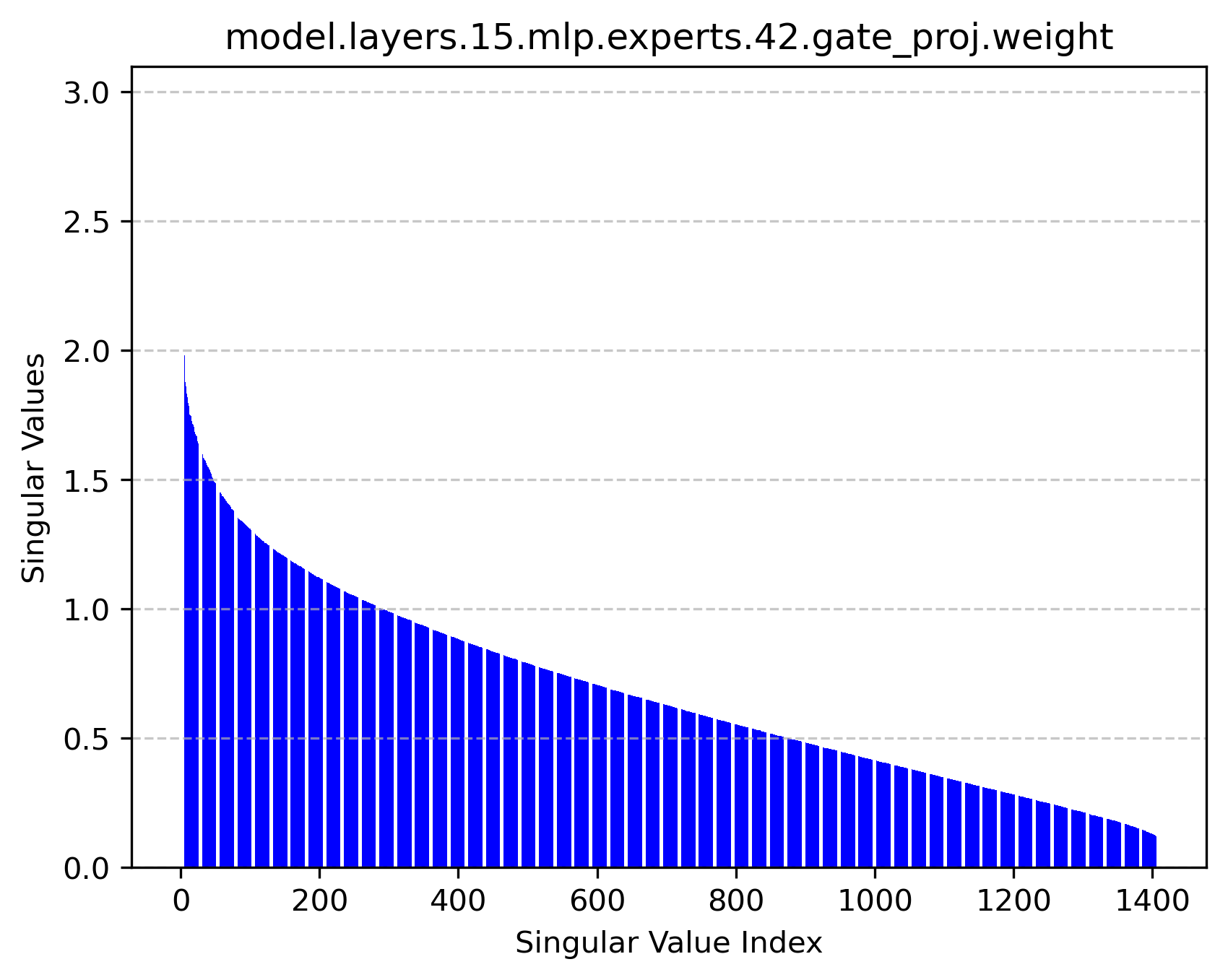
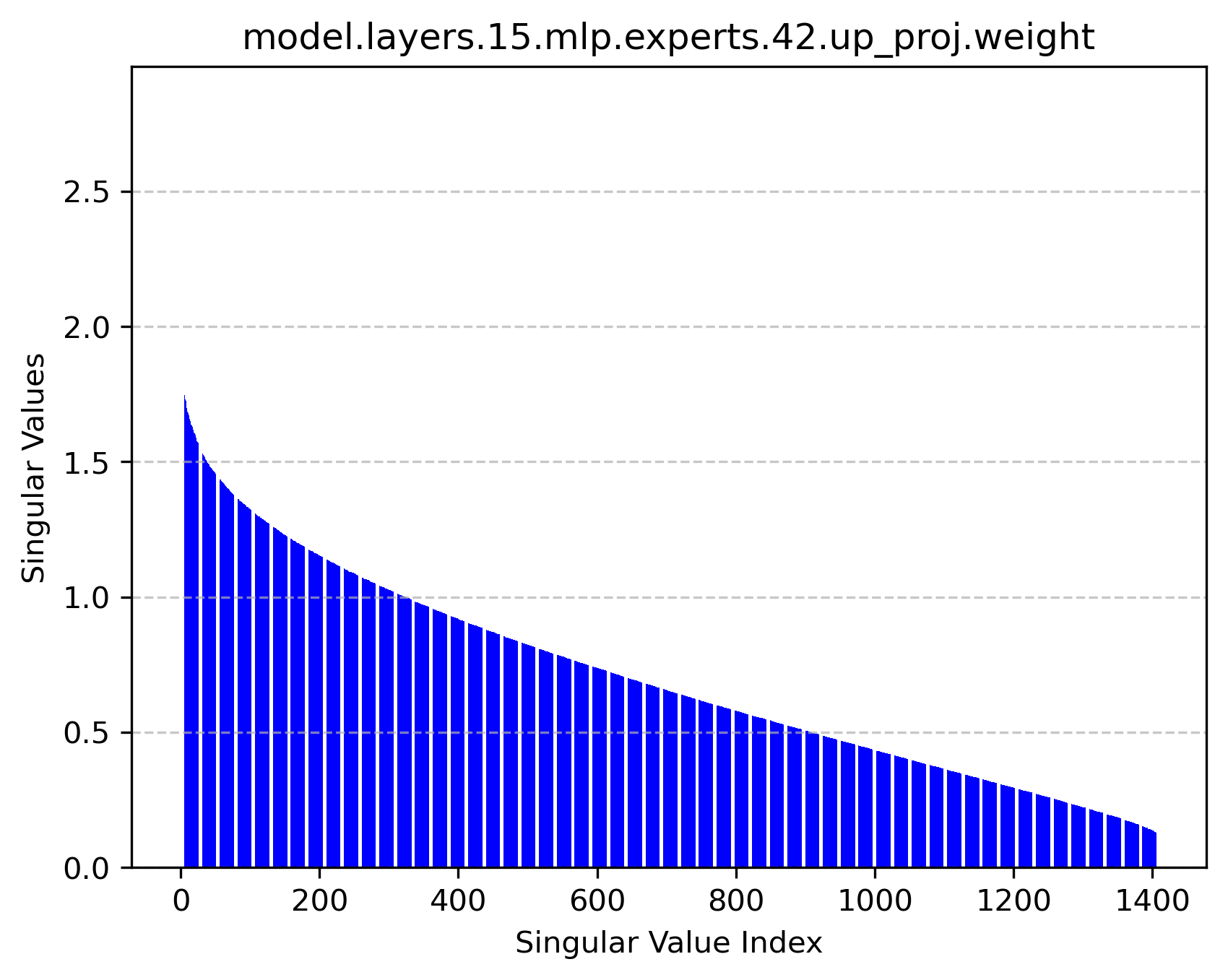
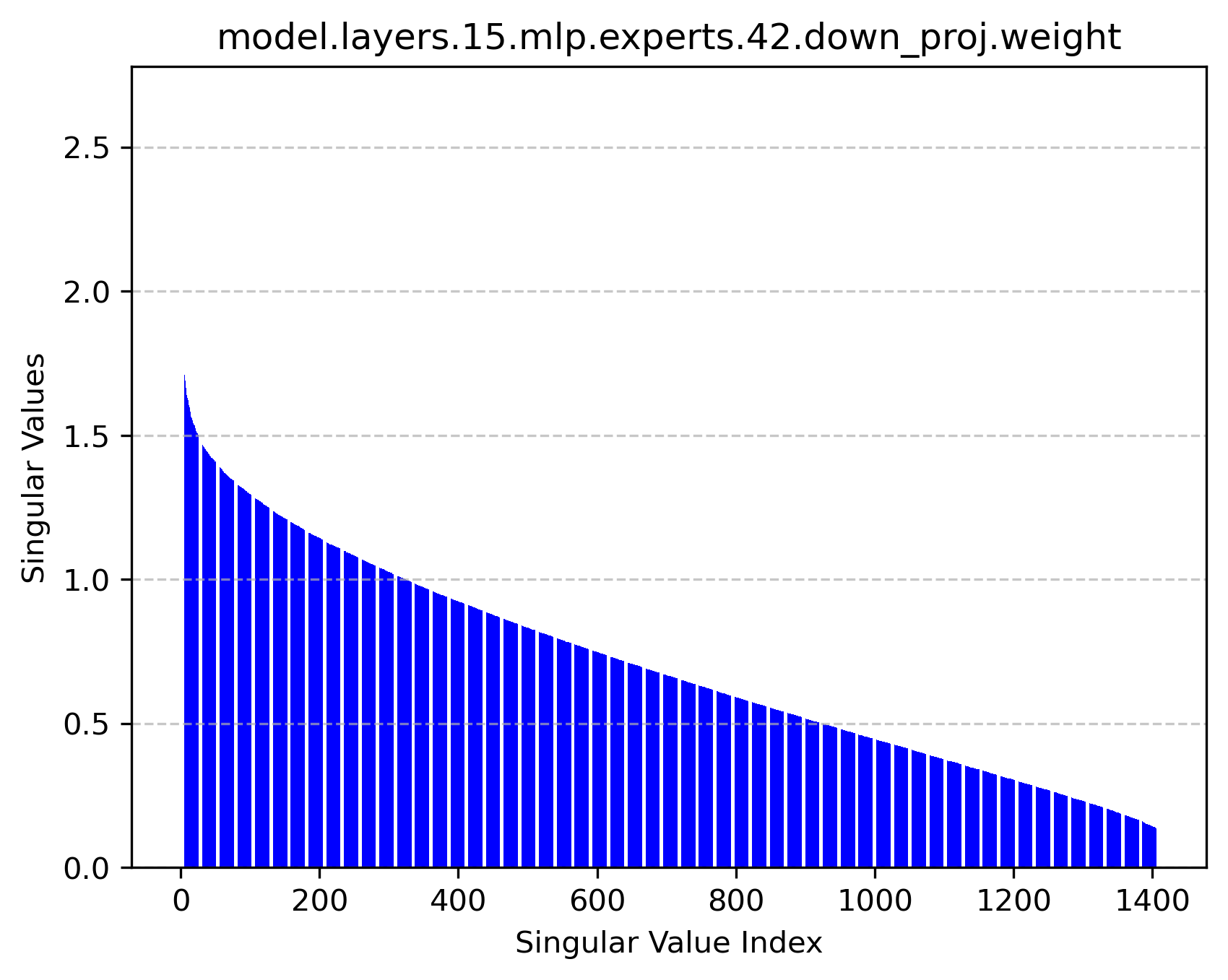
Figure 2: Singular value distributions of expert modules reveal rich high-rank structures, supporting the feasibility of factorized operation.

Conclusion

The Mixture of Latent Experts architecture significantly alleviates computational and memory demands inherent in traditional MoE models, maintaining functionality across diverse language processing tasks while utilizing fewer resources. The proposed transformation framework provides a principled approach to optimizing expert-specific parameters in LLMs. Future research directions could explore further optimizations around dynamic latent spaces and extensions of the factorization technique beyond FFN layers.

The implications of this structure also entail improved scalability in deploying LLMs across less resource-capable platforms, preserving computational power without compromising on the model's linguistic acuity.