Position: Solve Layerwise Linear Models First to Understand Neural Dynamical Phenomena (Neural Collapse, Emergence, Lazy/Rich Regime, and Grokking)

Abstract: In physics, complex systems are often simplified into minimal, solvable models that retain only the core principles. In machine learning, layerwise linear models (e.g., linear neural networks) act as simplified representations of neural network dynamics. These models follow the dynamical feedback principle, which describes how layers mutually govern and amplify each other's evolution. This principle extends beyond the simplified models, successfully explaining a wide range of dynamical phenomena in deep neural networks, including neural collapse, emergence, lazy and rich regimes, and grokking. In this position paper, we call for the use of layerwise linear models retaining the core principles of neural dynamical phenomena to accelerate the science of deep learning.

• The paper demonstrates that layerwise linear models analytically capture neural phenomena such as emergence, collapse, and regime transitions.
• It reveals how dynamical feedback between weight layers drives stage-like learning, mode competition, and low-rank feature bias.
• Empirical results confirm that controlling layer imbalance and initialization can toggle between lazy and rich regimes, affecting grokking.

Layerwise Linear Models as Foundational Tools for Understanding Neural Dynamical Phenomena

Overview and Motivation

This paper systematically advocates for the resolution of layerwise linear models—specifically, models that are multilinear in each layer’s parameters—as a critical prerequisite for understanding diverse, celebrated dynamical phenomena in deep neural networks (DNNs), including neural collapse, emergence, the lazy/rich regime dichotomy, and grokking. Drawing on strong analogies with minimal, tractable models in physics, the authors contend that the dynamical feedback mechanisms intrinsic to the layerwise structure, rather than the idiosyncrasies of non-linear activation functions, capture the essential nontrivial behaviors manifest in DNN training. The central thesis is formalized as the "dynamical feedback principle," which underpins the evolutionary interactions of weight layers and, through analytical tractability, reveals the generative mechanisms for major observed effects in practical DNNs.

Figure 1: Outline of the paper’s logical structure, systematically building intuition (green and yellow), formalizing in solvable layerwise linear models (blue), and connecting to empirical DNN phenomena (red).

The Dynamical Feedback Principle and Its Analytical Consequences

At the core of the dynamical analysis is the feedback coupling between weight layers. In two-layer linear networks (e.g., $f(x) = \sum_i x_i a_i b_i$), the time derivative of one parameter (say, $a_i$) is modulated by the magnitude of the corresponding parameter in the other layer ($b_i$), and vice versa. This amplifying mechanism leads to nontrivial nonlinear training dynamics, even in the absence of nonlinear activations. Unlike simple linear (single-layer) models—where each parameter evolves independently—the layerwise structure induces interactions that can result in rich-get-richer or poor-get-poorer behavior, mode competition, and stage-like learning. The commutativity of the layer coupling yields a conserved difference of magnitude-squared terms across layers.

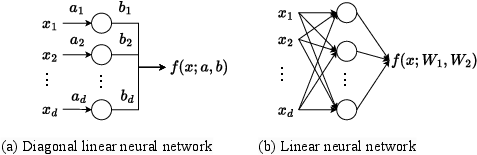
Figure 2: Depiction of layerwise linear models, illustrating diagonal and matrix-multilinear structures which govern the distinctive nonlinear training dynamics.

Emergence, Stage-Like Training, and Neural Scaling Laws

One primary observation relates to emergent behaviors, characterized by abrupt task or subtask acquisition during training—closely paralleling empirical phenomena in LLMs and multitask setups. The sigmoid-like dynamics predicted by layerwise linear models underpin the sequential, stage-like saturation of distinct feature modes: the fastest modes (highest variance or most frequent skills) are learned to completion before the next mode initiates significant growth. This delayed, prioritized learning is analytically solved and gives rise to sudden transitions in measured capabilities as resources (compute, data, parameters) cross specific thresholds.

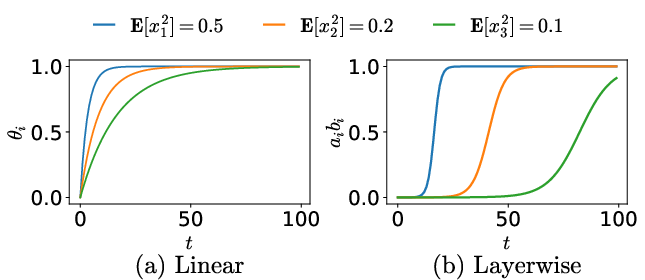
Figure 3: Dynamics comparison between a single-layer linear model (all modes saturate exponentially in parallel) and a diagonal linear neural network (modes sequentially saturate, inducing stage-like training).

Figure 4: Quantitative prediction of emergence: skill acquisition in multitask parity problems displays precise agreement between theory (layerwise linear model) and empirical DNN training.

Crucially, when the input distribution or task structure follows a power law, the collective effect of sigmoid transitions for “skills” induces empirically observed neural scaling laws. The abrupt “emergence” regions for individual skills integrate into power-law behavior across the aggregate loss or accuracy curves as a function of scale, consistent with observations in large transformer architectures.

Greedy Dynamics, Low-Rank Bias, and Neural Collapse

Extending the feedback mechanism to non-diagonal linear networks, the model yields an inductive “greedy” dynamic: training prioritizes learning the best-aligned (correlated) directions in data-label space, giving rise to a low-rank bias in the learned features. The resultant feature matrix, particularly at the output of the penultimate layer, becomes rank-constrained—yielding the neural collapse phenomenon. This is characterized by representations that cluster by class and form simplex equiangular tight frames, as seen empirically in DNNs trained for classification.

Figure 5: Mechanistic illustration of neural collapse—feature vectors cluster by class and align as simplex ETF structures.

Analytical derivations show that small or zero-initialization, together with overparameterization, ensures the minimization inherent in gradient flow induces a collapse of the network’s feature outputs to the minimum-rank solution fitting the data, even in the absence of explicit regularization. This dynamic is robust: the layerwise structure drives the rank minimization independent of nonlinear activation nuances.

Lazy and Rich Regimes: Layer Imbalance, Initialization, and Grokking

By examining the influence of layerwise parameter norm imbalance ($W_2 W_2^\top - W_1^\top W_1 = \lambda I$), the model admits precise control over whether the network operates in a “lazy” regime—where only one set of parameters effectively evolves and the network is limited to kernel regression-like behavior—or a “rich” regime that manifests active feature learning and mode competition. The transition is governed by both the initial relative magnitudes and the alignment between initial weight products and target scale. Analytical results, now unified across a lineage of work, demonstrate that sufficient imbalance or target scaling can suppress amplification, trapping the network in a lazy phase.

Figure 6: Two independent pathways to lazy dynamics: layer norm imbalance (a) and weight-to-target ratio (b), both quantifiably dictate the nonlinear vs. linear dynamics in training.

The authors connect this to the “grokking” phenomenon: delayed generalization in DNNs occurs in the lazy regime when the effective movement in feature space is suppressed; experimental and theoretical results concretely demonstrate that reducing the weight-to-target ratio or using targeted layerwise re-initialization eliminates grokking delays and promotes generalization.

Figure 7: Rich vs. lazy feature dynamics explained in function space: with poor initialization/lazy regime, features update uniformly with minimal effect; in rich regime, well-aligned features dominate learning dynamics (greedy competition).

Figure 8: Grokking delay abolished as weight-to-target ratio is reduced, confirmed both for shallow MLPs and transformers, underscoring the universal applicability of the underlying dynamical principle.

Figure 9: Empirical demonstration: modulating the weight-to-target ratio, input/output scaling, or initialization, in MLPs trained on real data, transitions models out of grokking regimes and accelerates learning.

Theoretical and Practical Implications

The evidence and explicit solvability provided by layerwise linear models reveal that many intricate phenomena in practical DNNs owe their existence to the nontrivial dynamical coupling between layers, rather than to nonlinearity per se. This suggests that for the taxonomy of observed behaviors during training—including abrupt skill emergence, low-rank feature collapse, and regime transitions—a comprehensive analysis of the multilinear structure suffices as a starting point. The nonlinearity, particularly ReLU, often acts as a perturbative modification on top of this base, modulating expressivity but not fundamentally changing qualitative dynamical outcomes.

The authors highlight several practical recommendations and conjectures:

• For unexplained dynamical events in DNN training, prior analysis of the corresponding layerwise linear dynamics should be prioritized.
• Improvements in regularization, generalization, or task specialization may likely arise from initializations and architectural modifications that explicitly promote or leverage rich dynamical regimes.
• Nonlinearities or architectural augmentations (e.g., batch normalization, skip connections) can often be interpreted as controlled perturbations to this base, and their effects systematically analyzed within this framework.

Directions for Future Research

• Formal refinement of when and how nonlinearity, beyond the linear regime, introduces qualitative novelties relative to the feedback principle baseline.
• Exploitation of the analytical tractability for efficient routine diagnostics in large-scale practical DNN training, including online monitoring of regime transitions (e.g., grokking).
• Perturbative extensions and renormalization-group-like approaches to systematically include nonlinear corrections atop layerwise linear models.
• Deeper investigation of inductive biases (e.g., low-rank collapse), their relationship to generalization, and when they may or may not be beneficial in practice.

Conclusion

This paper forcefully demonstrates, with explicit analytical solutions and matching empirical evidence, that the core dynamic phenomena seen across modern deep learning—from emergence and neural scaling laws to neural collapse, lazy/rich dichotomies, and grokking—are generically explained by the intrinsic feedback dynamics of layerwise linear models. Extending the physics tradition of minimal yet unifying solvable models, this approach offers a disciplined, tractable, and counterintuitively powerful basis for future theoretical and methodological advances in deep learning.