Seed-Prover: Deep and Broad Reasoning for Automated Theorem Proving (2507.23726v2)

Abstract: LLMs have demonstrated strong mathematical reasoning abilities by leveraging reinforcement learning with long chain-of-thought, yet they continue to struggle with theorem proving due to the lack of clear supervision signals when solely using natural language. Dedicated domain-specific languages like Lean provide clear supervision via formal verification of proofs, enabling effective training through reinforcement learning. In this work, we propose \textbf{Seed-Prover}, a lemma-style whole-proof reasoning model. Seed-Prover can iteratively refine its proof based on Lean feedback, proved lemmas, and self-summarization. To solve IMO-level contest problems, we design three test-time inference strategies that enable both deep and broad reasoning. Seed-Prover proves $78.1\%$ of formalized past IMO problems, saturates MiniF2F, and achieves over 50\% on PutnamBench, outperforming the previous state-of-the-art by a large margin. To address the lack of geometry support in Lean, we introduce a geometry reasoning engine \textbf{Seed-Geometry}, which outperforms previous formal geometry engines. We use these two systems to participate in IMO 2025 and fully prove 5 out of 6 problems. This work represents a significant advancement in automated mathematical reasoning, demonstrating the effectiveness of formal verification with long chain-of-thought reasoning.

• The paper presents Seed-Prover, a formal reasoning system that uses LLMs for whole-proof generation with modular, lemma-style proofs.
• It introduces iterative proof refinement and a three-tiered inference strategy to balance deep and broad automated theorem proving.
• Empirical results demonstrate state-of-the-art performance on challenging benchmarks including IMO, MiniF2F, PutnamBench, and CombiBench.

Seed-Prover: Deep and Broad Reasoning for Automated Theorem Proving

Introduction and Motivation

The paper introduces Seed-Prover, a formal reasoning system that leverages LLMs for automated theorem proving (ATP) in Lean 4, with a particular focus on deep and broad mathematical reasoning. The work addresses the limitations of natural language-based LLMs in mathematical proof verification, emphasizing the necessity of formal languages for clear supervision and effective RL-based training. The system is evaluated on a range of challenging mathematical benchmarks, including the International Mathematical Olympiad (IMO), MiniF2F, PutnamBench, and CombiBench, and is complemented by Seed-Geometry, a dedicated neuro-symbolic geometry engine.

System Architecture and Methodology

Lemma-Style Whole-Proof Generation

Seed-Prover departs from traditional step-level provers by adopting a whole-proof generation paradigm, with a strong emphasis on lemma-style proving. The model is trained to generate intermediate lemmas before attempting the main theorem, enabling modularity, independent verification, and the reuse of proven results across different inference trajectories. This approach is operationalized via a lemma pool, which tracks lemma statements, proofs, proof difficulties, and dependency relations, facilitating both retrieval and sampling during inference.

Figure 1: An example of whole proof and lemma-style proof in Lean 4, illustrating the modularity and compositionality of lemma-centric reasoning.

Iterative Proof Refinement and Conjecture Proposing

Seed-Prover incorporates iterative proof refinement, leveraging Lean compiler feedback and self-summarization to correct syntactic and logical errors. The system also features a conjecture proposer module, which generates a diverse set of candidate properties (conjectures) for a given problem, supporting broad exploration of the problem space. This is particularly effective for contest-level problems where direct solution is infeasible, and useful properties must be discovered and proved incrementally.

Multi-Stage RL Training and Diverse Prompting

The training pipeline employs multi-stage, multi-task RL (based on VAPO), with rewards tied to successful formal proof completion. The model is exposed to a diverse set of prompts, including natural language hints, failed attempts, summaries, and Lean feedback, enhancing its robustness and adaptability. Problems that are too easy or too difficult are filtered or decomposed, respectively, to optimize the RL curriculum.

Test-Time Inference Strategies

Seed-Prover introduces a three-tiered inference strategy to balance depth and breadth of reasoning:

• Light Setting: Iterative refinement of proof attempts with a moderate sample budget, suitable for problems solvable with limited exploration.
• Medium Setting: Nested refinement, where difficult lemmas are targeted with additional inner refinement, enabling the resolution of structurally complex proofs.
• Heavy Setting: Large-scale conjecture generation and proof attempts, with thousands of conjectures proposed and selectively proved or disproved, followed by integration of top-ranked lemmas into the final proof.

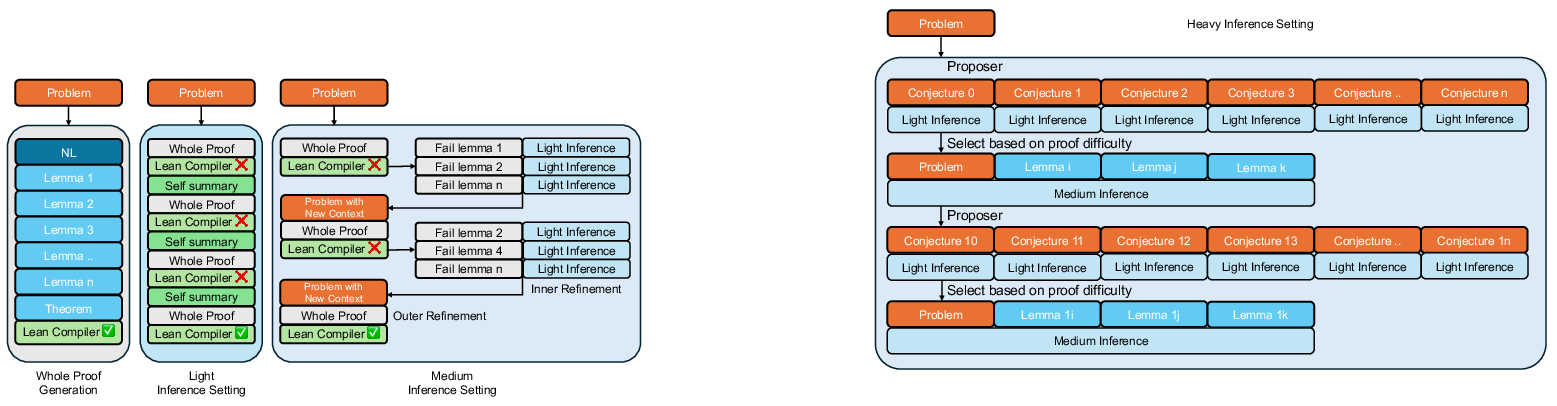
  Figure 2: The workflows of single-pass whole proof generation, light, and medium inference settings, highlighting the iterative and nested refinement processes.

  

  Figure 3: The workflow of heavy inference setting, illustrating large-scale conjecture generation, lemma pool accumulation, and integration for final proof synthesis.

Seed-Geometry: Neuro-Symbolic Geometry Reasoning

Seed-Geometry is a neuro-symbolic geometry engine designed to address the lack of geometry support in Lean. It features:

• An extended domain-specific language for concise geometric constructions, including composite actions for complex constructions.
• A high-performance C++ backend for the reasoning engine, yielding a 100x speedup over previous Python implementations.
• A Seed-family LLM trained on a massive dataset of 230 million unique geometry problems, focusing on auxiliary construction completion.
• Distributed, beam-search-based inference with asynchronous reasoning, enabling efficient large-scale search in the geometry space.

Seed-Geometry demonstrates superior performance on IMO geometry problems and the more challenging IMO shortlist, outperforming AlphaGeometry 2, particularly on proof-based problems.

Empirical Results

Seed-Prover achieves state-of-the-art results across multiple formal mathematics benchmarks:

• IMO 2025: Proved 5 out of 6 problems (4/6 during the official contest, 5/6 post-competition), matching or exceeding prior formal systems.
• Past IMO Problems: 78.1% success rate on 155 formalized problems, with strong performance across algebra, number theory, and combinatorics.
• MiniF2F: 99.6% on MiniF2F-test and 100% on MiniF2F-valid, saturating the benchmark.
• PutnamBench: 331/657 problems solved, a substantial improvement over previous SOTA (86/657).
• CombiBench: 30% success rate, tripling the previous best.
• MiniCTX-v2: 81.8% success rate, nearly doubling the previous best.

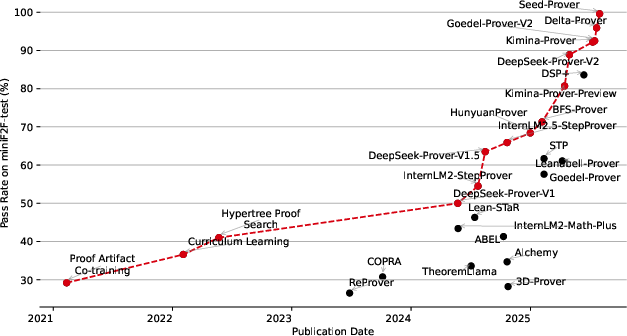
  Figure 4: Growth in MiniF2F-Test performance over time, demonstrating the rapid progress and eventual saturation achieved by Seed-Prover.

Notably, the system demonstrates the ability to handle extremely long and complex proofs (exceeding 1000 lines), and the heavy inference setting enables the solution of problems previously considered intractable for LLM-based provers.

Practical and Theoretical Implications

The integration of formal languages, lemma-centric reasoning, and scalable inference strategies in Seed-Prover establishes a new paradigm for ATP with LLMs. The modularity and compositionality of lemma-style proofs facilitate proof reuse and independent verification, addressing key challenges in scaling formal mathematics. The neuro-symbolic approach in Seed-Geometry demonstrates the efficacy of combining LLMs with high-performance symbolic engines for domain-specific reasoning.

The strong empirical results, particularly the ability to solve the majority of IMO and Putnam-level problems, indicate that formal LLM-based provers are approaching the threshold of practical utility for research-level mathematics. The system's reliance on formal verification ensures correctness and reliability, in contrast to natural language-based approaches that suffer from unverifiable reasoning steps.

Future Directions

The paper suggests several avenues for future research:

• Further integration of formal systems and LLMs to tackle open mathematical conjectures.
• Extension of the neuro-symbolic approach to other mathematical domains beyond geometry.
• Optimization of inference strategies for combinatorics and other domains where current performance lags.
• Exploration of proof simplification, statement negation, and multi-concurrency support for large-scale formalization projects.

Conclusion

Seed-Prover and Seed-Geometry represent significant advancements in formal automated theorem proving with LLMs. The systems' ability to perform deep and broad reasoning, modular proof synthesis, and efficient large-scale search establishes new benchmarks across a range of mathematical domains. The results underscore the importance of formal languages and neuro-symbolic integration for reliable, scalable ATP, and point toward the increasing feasibility of AI-assisted formal mathematics at the research frontier.