Modeling and hexahedral meshing of cerebral arterial networks from centerlines

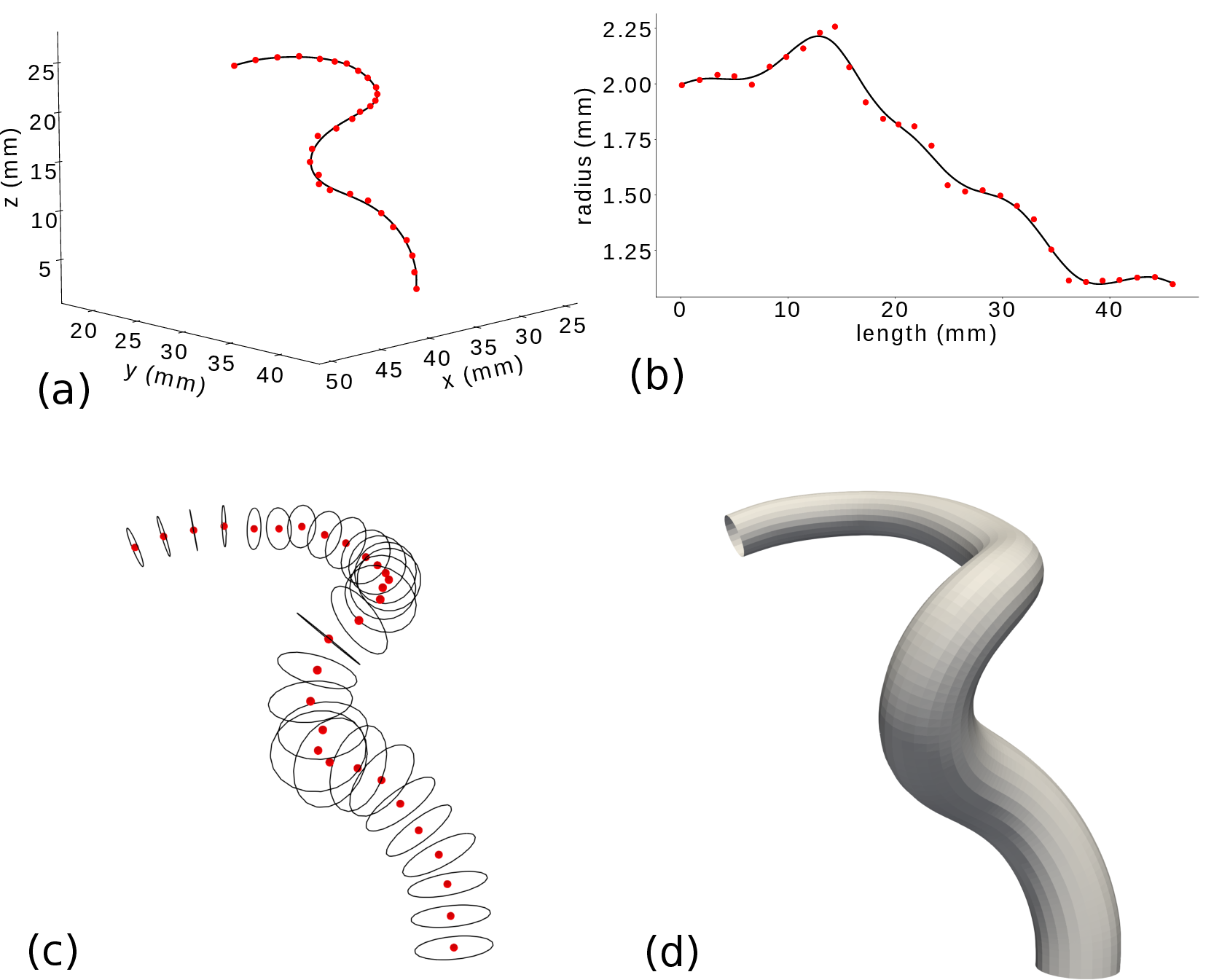
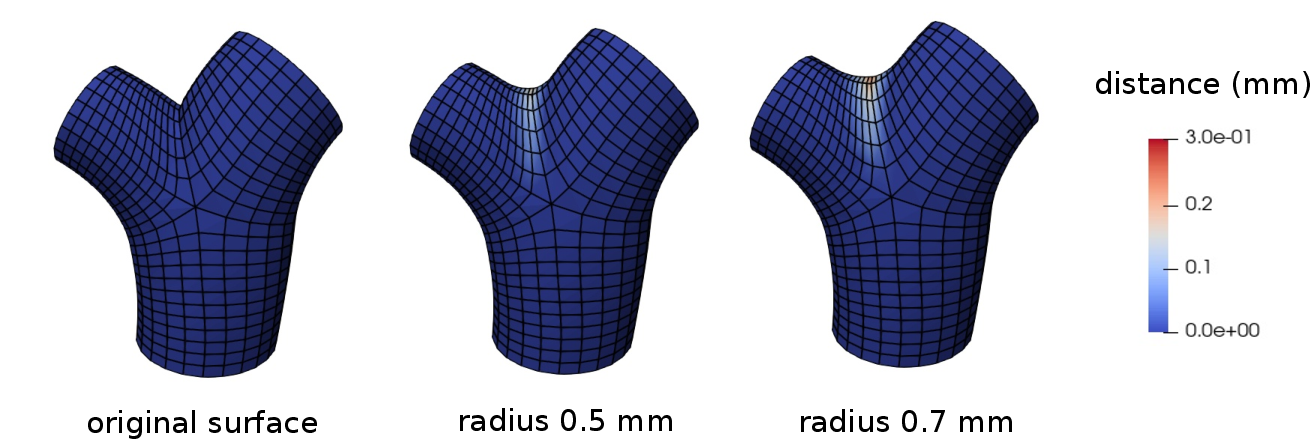
Abstract: Computational fluid dynamics (CFD) simulation provides valuable information on blood flow from the vascular geometry. However, it requires extracting precise models of arteries from low-resolution medical images, which remains challenging. Centerline-based representation is widely used to model large vascular networks with small vessels, as it encodes both the geometric and topological information and facilitates manual editing. In this work, we propose an automatic method to generate a structured hexahedral mesh suitable for CFD directly from centerlines. We addressed both the modeling and meshing tasks. We proposed a vessel model based on penalized splines to overcome the limitations inherent to the centerline representation, such as noise and sparsity. The bifurcations are reconstructed using a parametric model based on the anatomy that we extended to planar n-furcations. Finally, we developed a method to produce a volume mesh with structured, hexahedral, and flow-oriented cells from the proposed vascular network model. The proposed method offers better robustness to the common defects of centerlines and increases the mesh quality compared to state-of-the-art methods. As it relies on centerlines alone, it can be applied to edit the vascular model effortlessly to study the impact of vascular geometry and topology on hemodynamics. We demonstrate the efficiency of our method by entirely meshing a dataset of 60 cerebral vascular networks. 92% of the vessels and 83% of the bifurcations were meshed without defects needing manual intervention, despite the challenging aspect of the input data. The source code is released publicly.

• The paper presents a novel vessel modeling framework using penalized splines to robustly fit noisy centerline data.
• It details a complete pipeline including bifurcation reconstruction and O-grid-based structured hexahedral meshing for improved CFD performance.
• Experimental results show high mesh quality with 71% of bifurcation cells and 95.7% of vessel cells achieving scaled Jacobian values above 0.9.

Hexahedral Meshing of Cerebral Arterial Networks from Centerlines

This paper addresses the challenging problem of generating high-quality hexahedral meshes for CFD simulations of cerebral arterial networks, directly from centerline representations. The method overcomes limitations inherent in centerline data, such as noise and sparsity, and provides a robust and automated approach applicable to large vascular networks. The authors present a complete pipeline encompassing vessel modeling, bifurcation reconstruction, and hexahedral volume mesh generation, offering improvements in mesh quality and robustness compared to existing techniques.

Vessel Modeling with Penalized Splines

The paper introduces a novel vessel model based on penalized splines to approximate centerline data. This approach addresses the limitations of traditional centerline representations, including noise and sparsity. The spline function $s(u)$ is defined using basis spline functions $N_{i, p}(u)$ of order $p$ and control points $P_i$ as:

$s(u) = \sum_{i = 0}^{n - 1} N_{i, p}(u) P_{i}$

The control points are optimized using a two-term cost function that balances closeness to data points and smoothness, controlled by a parameter $\lambda$:

$f(P_{0},..., P_{n - 1}) = \sum_{k = 0}^{m-1}{|D_{k} - s(t_{k})|^{2} + \lambda \sum_{j = 2}^{n}{(P_{j}-2 P_{j-1}+P_{j-2})^2}$

Figure 1: Approximation of a noisy centerline using penalized splines, demonstrating the method's robustness to noise and low sampling rates for both spatial coordinates and radius.

The method approximates spatial coordinates and radii separately, optimizing control points using a two-step algorithm and minimizing the Akaike criterion to determine optimal $\lambda$ values. This approach demonstrates improved robustness to noise and low sampling rates compared to conventional methods.

Bifurcation Modeling and Parameter Estimation

The paper employs a parametric bifurcation model based on the work of Zakaria et al. [2008], which represents bifurcations as two merged tubes defined by five cross-sections: a shared inlet, separate apical sections, and outlet sections (Figure 2).

Figure 2: Illustration of Zakaria's five cross-sections bifurcation model, which is based on anatomical parameters for realistic bifurcation representation.

A key contribution is an algorithm to estimate bifurcation parameters directly from centerline data. Independent vessel models are created for each branch, and the apex is computed as the intersection of the vessel surfaces (Figure 3). Apical and outlet sections are then determined based on the apex position. To ensure continuity, the end tangents of the vessels match the normals of the bifurcation cross-sections by introducing constraints in the spline approximation.

Figure 3: The process of estimating bifurcation parameters from centerline data, involving independent vessel modeling and apex computation for accurate parameter extraction.

Structured Hexahedral Meshing

The paper details a method for generating structured hexahedral volume meshes with flow-oriented cells from the parametric model. This involves decomposing the bifurcation into three branches using separation planes, creating an initial mesh grid, and projecting nodes radially onto the vessel surfaces. The geometric decomposition of the bifurcation model is shown in (Figure 4).

Figure 4: A geometric decomposition of the bifurcation model, illustrating the separation planes used to divide the bifurcation into three branches for structured meshing.

The initial mesh grid is created by connecting end cross-sections to the separation planes with successive cross-sections, where the nodes of the end cross-sections and the nodes of the separation half-sections are connected to form the initial mesh grid (Figure 5).

Figure 5: Computation of nodes for end cross-sections and separation planes, showing the structured arrangement crucial for generating a hexahedral mesh.

The initial surface mesh and mesh after projection are shown in Figure 6.

Figure 6: Comparison of initial and projected surface meshes, highlighting the impact of initialization on the final mesh geometry and quality.

A relaxation step is applied to improve cell quality and continuity by Laplacian smoothing and back-projection (Figure 7). The apex region is smoothed using a 2D method involving projection onto a plane and rolling a circle along the curves to preserve cell quality.

Figure 7: Iterative relaxation of the bifurcation mesh, demonstrating improvement in cell quality as measured by the scaled Jacobian metric.

The apex smoothing pipeline is shown in Figure 8, and examples of apex smoothing with different radius of curvature values is shown in Figure 9.

Figure 8: An illustration of the apex smoothing pipeline, detailing the process of refining the apical region of the bifurcation mesh.

Figure 9: Apex smoothing with different curvature radii, illustrating the control over local geometry and the distance to the original mesh.

This approach is generalized to planar n-furcations by adjusting the decomposition scheme to compute $n+1$ separation planes (Figure 10). The O-grid pattern is used to convert the quadrangular surface mesh into a hexahedral volume mesh, as shown in Figure 11.

Figure 10: A parametric model and branch decomposition scheme for a trifurcation, showcasing the method's ability to handle more complex branching patterns.

Figure 11: The O-grid pattern for volume meshing, which ensures structured hexahedral cells suitable for CFD simulations.

Experimental Results and Applications

The paper presents evaluations of vessel modeling and comparisons with state-of-the-art meshing methods. Results demonstrate the robustness of the penalized spline approximation method, with lower RMSE values for spatial coordinates, radius, and curvature compared to non-penalized methods. The quality of the meshes generated is assessed via the scaled Jacobian metric, with $71\%$ of bifurcation cells and $95.7\%$ of vessel cells achieving values greater than 0.9 (Figure 12). The distribution of the scaled Jacobian values of the mesh cells are shown in Figure 12.

Figure 12: Histograms showing the distribution of scaled Jacobian values for mesh cells, indicating high overall mesh quality with minimal negative values.

Several applications are explored, including deformation for aneurysm modeling, topology and geometry editing, and large cerebral arterial network meshing. The method is applied to a dataset of 60 patients from the BraVa database, with $83\%$ of bifurcations and $92\%$ of vessels successfully meshed. CFD simulations are conducted to demonstrate the applicability of the generated meshes for blood flow studies, showing improved convergence and reduced computational cost compared to tetrahedral meshes.

Conclusion

The paper presents a comprehensive framework for generating high-quality hexahedral meshes of cerebral arterial networks from centerline data. The method addresses limitations in existing techniques and offers improvements in robustness, mesh quality, and applicability to large-scale networks. The release of the source code enhances the impact of this work, facilitating further research and application in CFD simulations of vascular systems. Future work could focus on non-planar n-furcations, incorporating more anatomical constraints, and refining the modeling method to enhance robustness.