Geometric Operator Learning with Optimal Transport (2507.20065v1)

Abstract: We propose integrating optimal transport (OT) into operator learning for partial differential equations (PDEs) on complex geometries. Classical geometric learning methods typically represent domains as meshes, graphs, or point clouds. Our approach generalizes discretized meshes to mesh density functions, formulating geometry embedding as an OT problem that maps these functions to a uniform density in a reference space. Compared to previous methods relying on interpolation or shared deformation, our OT-based method employs instance-dependent deformation, offering enhanced flexibility and effectiveness. For 3D simulations focused on surfaces, our OT-based neural operator embeds the surface geometry into a 2D parameterized latent space. By performing computations directly on this 2D representation of the surface manifold, it achieves significant computational efficiency gains compared to volumetric simulation. Experiments with Reynolds-averaged Navier-Stokes equations (RANS) on the ShapeNet-Car and DrivAerNet-Car datasets show that our method achieves better accuracy and also reduces computational expenses in terms of both time and memory usage compared to existing machine learning models. Additionally, our model demonstrates significantly improved accuracy on the FlowBench dataset, underscoring the benefits of employing instance-dependent deformation for datasets with highly variable geometries.

• The paper introduces an OT framework that embeds surface meshes into a canonical latent space while preserving global geometric measures.
• It leverages both Monge and Kantorovich formulations via methods like PPMM and Sinkhorn to achieve instance-dependent, measure-preserving embeddings.
• Empirical results demonstrate that OTNO achieves superior convergence rates and computational savings compared to methods such as Geo-FNO and GINO.

Geometric Operator Learning with Optimal Transport: An Expert Analysis

Introduction and Motivation

The paper "Geometric Operator Learning with Optimal Transport" (2507.20065) introduces a principled framework for operator learning on complex geometric domains, with a focus on partial differential equations (PDEs) arising in computational fluid dynamics (CFD). The central innovation is the integration of optimal transport (OT) theory into the geometric encoding process for neural operators, enabling instance-dependent, measure-preserving embeddings of surface meshes into canonical latent spaces. This approach addresses key limitations of prior methods—such as Geo-FNO and GINO—by providing both flexibility and computational efficiency, particularly for high-dimensional, surface-dominated problems.

Methodological Framework

Geometry Embedding via Optimal Transport

The core methodological advance is the reformulation of geometry embedding as an OT problem. Surface meshes are interpreted as continuous mesh density functions, and the embedding is realized by solving for an OT map or plan that transports the physical mesh density to a uniform density on a reference latent domain (e.g., a sphere or torus). This process is instance-specific, in contrast to previous approaches that learn a shared deformation or rely on fixed graph structures.

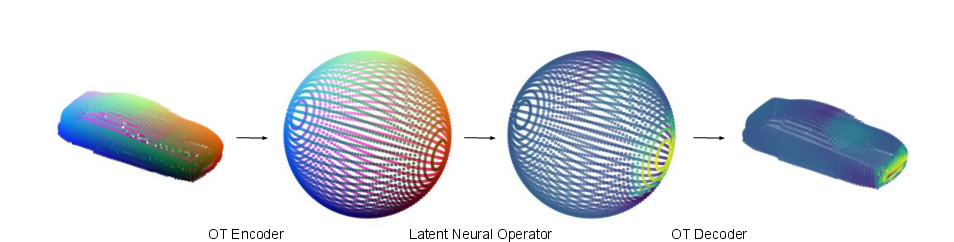
Figure 1: Illustration of the optimal transport neural operator (OTNO) pipeline, showing OT-based encoding, latent neural operator computation, and OT-based decoding.

The OT embedding preserves global geometric measures, which is essential for the accurate computation of integral operators in neural operator architectures. The paper leverages both the Monge (map-based) and Kantorovich (plan-based) formulations, implemented via the Projection Pursuit Monge Map (PPMM) and the Sinkhorn algorithm, respectively.

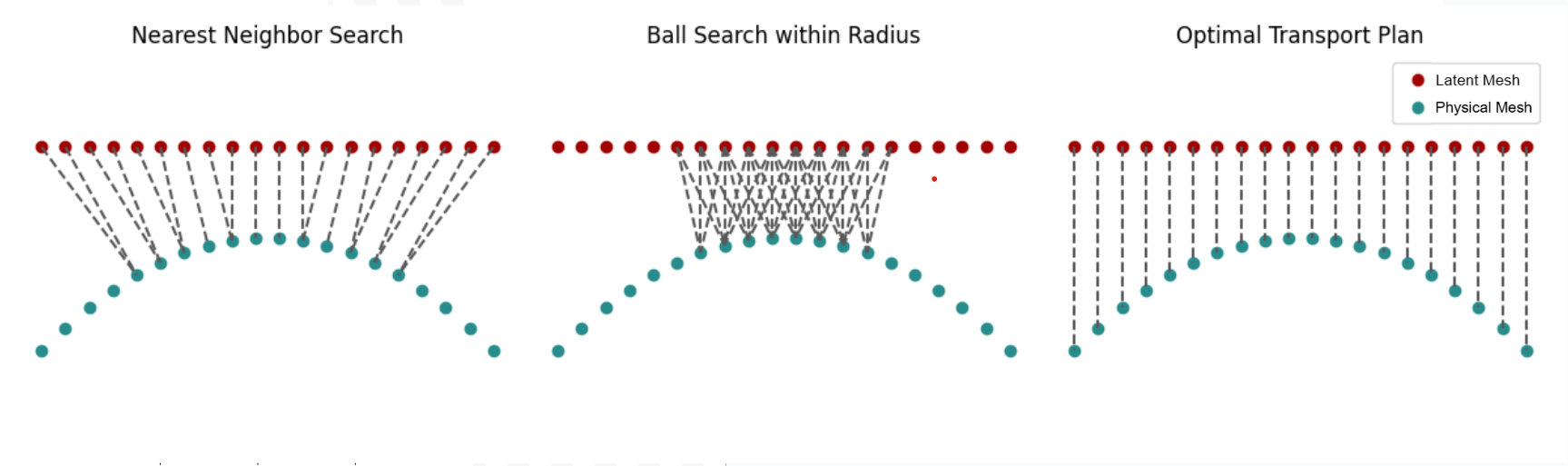
Figure 2: OT plans as bi-partite graphs, contrasting OT-based mapping with ball and nearest-neighbor strategies; OT preserves global measure, critical for operator learning.

Sub-Manifold Method and Dimension Reduction

A significant contribution is the sub-manifold method, which restricts operator learning to the boundary (surface) of the domain, reducing the ambient dimension by one. For many CFD applications, such as RANS simulations on automotive surfaces, the solution of interest (e.g., pressure, shear) is defined on the 2D surface embedded in 3D. The OT-based embedding enables computations to be performed directly in a 2D latent space, yielding substantial reductions in computational cost.

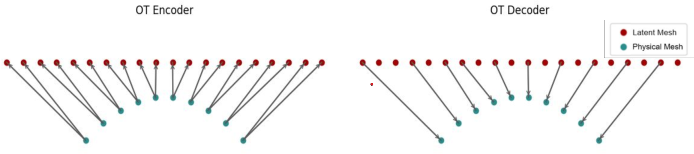
Figure 3: Simple illustration of the OT encoder and decoder, mapping between boundary sampling points and the latent computational grid.

OTNO Architecture and Implementation

The Optimal Transport Neural Operator (OTNO) architecture consists of:

• OT Encoder: Computes the OT map/plan from the latent grid to the physical mesh.
• Latent Neural Operator: Applies a (Spherical) Fourier Neural Operator (FNO) on the latent grid.
• OT Decoder: Maps the latent solution back to the physical mesh using the inverse OT map or plan.

The encoder/decoder strategies are carefully designed to balance accuracy and memory efficiency, with ablation studies demonstrating the superiority of the "Mean" strategy (nearest neighbor in physical mesh) over direct matrix multiplication or "Max" strategies.

Empirical Results

Convergence and Efficiency

OTNO demonstrates superior convergence rates and computational efficiency compared to GINO and Geo-FNO across multiple mesh resolutions.

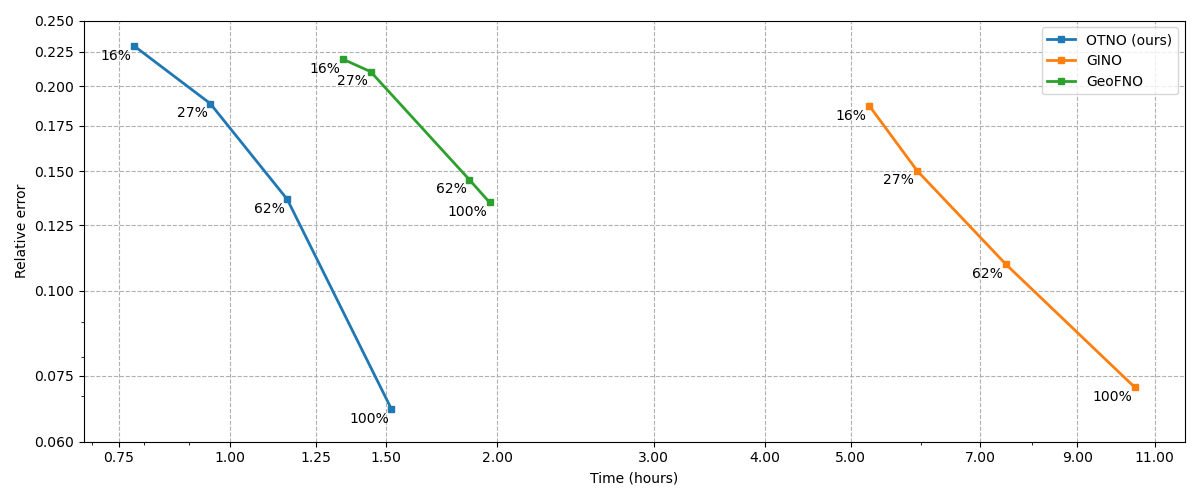
Figure 4: Convergence rates for OTNO, GINO, and Geo-FNO under varying mesh downsampling; OTNO achieves the fastest exponential convergence (rate 1.85).

3D Car Datasets: ShapeNet-Car and DrivAerNet-Car

On ShapeNet-Car, OTNO(Plan) achieves a relative L2 error of 6.70%, outperforming GINO (7.21%) and reducing both total runtime and GPU memory usage by factors of 8 and 7, respectively.

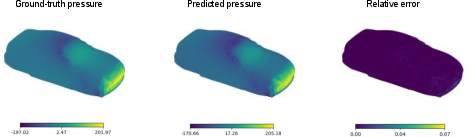
Figure 5: Visualization of OTNO pressure field predictions on the ShapeNet-Car dataset.

On DrivAerNet-Car, OTNO(Plan) halves the MSE compared to RegDGCNN, with 5x speedup and 24x lower memory usage. Compared to GINO, OTNO(Plan) achieves slightly better accuracy with 4x lower runtime and 5x lower memory.

Diverse Geometries: FlowBench Dataset

On the FlowBench dataset, which features highly variable 2D shapes, OTNO achieves significantly lower errors than FNO and GINO under both global (M1) and boundary (M2) metrics. Notably, Geo-FNO fails to generalize, with errors exceeding 60%, highlighting the advantage of instance-dependent OT embeddings.

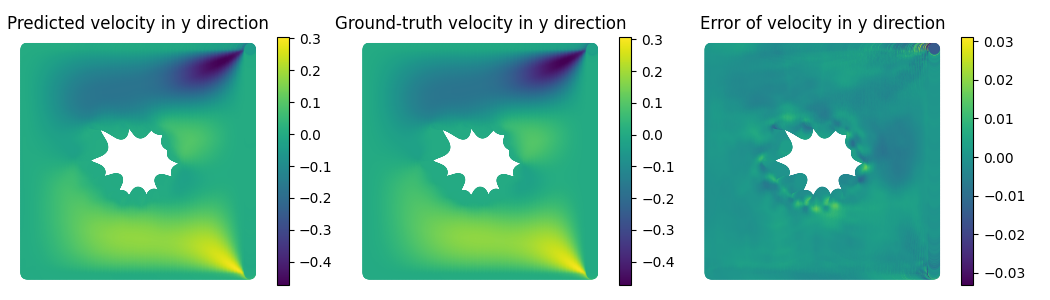
Figure 6: OTNO results on the FlowBench dataset, demonstrating robust performance across diverse geometries.

Ablation Studies

• Encoder/Decoder Strategies: The "Mean" strategy (nearest neighbor) yields the best accuracy and memory efficiency.
• Latent Mesh Shape: A torus latent grid outperforms spheres and planes, despite topological mismatch with the physical surface.
• Latent Mesh Size: Expanding the latent mesh (expansion factor $\alpha=3$) improves accuracy up to a point.
• Normal Features: Including cross-product of latent and physical normals as features enhances performance.
• OT Algorithm Choice: Sinkhorn-based OTNO(Plan) achieves higher accuracy but with $O(n^2)$ complexity; PPMM-based OTNO(Map) is more scalable ($O(n^{3/2}\log n)$) but less accurate.

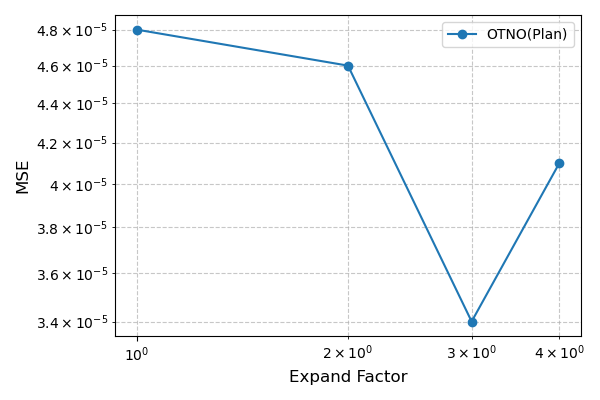
Figure 7: Ablation of latent mesh expansion factor for OTNO(Plan) on ShapeNet and DrivAerNet datasets.

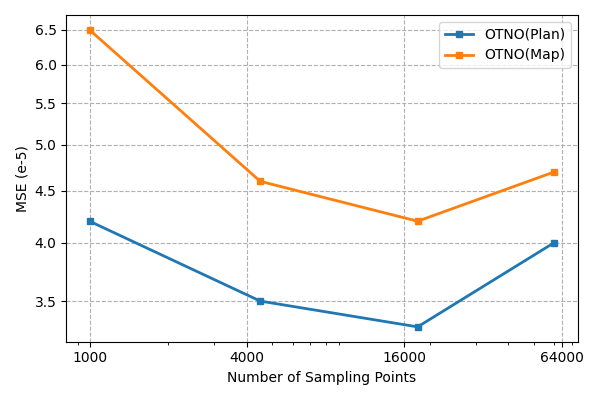
Figure 8: Ablation of sampling mesh size for OTNO(Map) and OTNO(Plan) on DrivAerNet, showing error and time scaling.

Theoretical and Practical Implications

Measure-Preserving Embeddings

The use of OT ensures that the geometric embedding preserves global measures, which is critical for the stability and accuracy of neural operators that rely on integral kernels. This property is not guaranteed by conformal or diffeomorphic mappings, which may preserve angles or topology but not measure.

Instance-Dependent Deformation

By solving the OT problem for each instance, OTNO can adapt to highly variable geometries, a key advantage over methods that learn a shared deformation or rely on fixed graph structures. This is particularly important for datasets with large intra-class variability, as demonstrated on FlowBench.

Dimension Reduction and Computational Savings

The sub-manifold method enables computations to be performed in a lower-dimensional latent space, yielding substantial reductions in both runtime and memory. For surface-dominated problems, this leads to 2x-8x improvements in efficiency over prior ML methods, and orders-of-magnitude speedup over traditional CFD solvers.

Topology and Latent Space Selection

Empirical results indicate that the optimal latent manifold need not match the topology of the physical surface. In fact, a torus latent grid outperforms spheres, despite the lack of topological equivalence. This challenges the conventional wisdom of enforcing topological consistency in geometric embeddings.

Limitations and Future Directions

• Scalability: The $O(n^2)$ complexity of Sinkhorn-based OTNO(Plan) limits scalability for very large point clouds. PPMM-based OTNO(Map) offers better scaling but at the cost of accuracy.
• Latent Manifold Selection: The choice of latent manifold significantly impacts performance, but optimal selection criteria remain an open question.
• Extension to Volumetric Problems: While the framework excels for surface-dominated problems, its extension to volumetric PDEs or problems with non-surface-dominated solutions warrants further investigation.
• Sub-Quadratic OT Algorithms: Developing more efficient OT solvers with sub-quadratic complexity and high accuracy is a promising research direction.

Conclusion

The integration of optimal transport into geometric operator learning provides a unified, flexible, and efficient framework for neural operator models on complex domains. The OTNO architecture achieves state-of-the-art accuracy and efficiency on challenging CFD benchmarks, particularly for surface-dominated problems. Theoretical insights into measure preservation, instance-dependent deformation, and latent space selection have broad implications for geometric deep learning and scientific machine learning. Future work should focus on scalable OT algorithms and principled latent manifold design to further advance the applicability of operator learning in scientific computing.