SETOL: A Semi-Empirical Theory of (Deep) Learning (2507.17912v2)

Abstract: We present a SemiEmpirical Theory of Learning (SETOL) that explains the remarkable performance of State-Of-The-Art (SOTA) Neural Networks (NNs). We provide a formal explanation of the origin of the fundamental quantities in the phenomenological theory of Heavy-Tailed Self-Regularization (HTSR): the heavy-tailed power-law layer quality metrics, alpha and alpha-hat. In prior work, these metrics have been shown to predict trends in the test accuracies of pretrained SOTA NN models, importantly, without needing access to either testing or training data. Our SETOL uses techniques from statistical mechanics as well as advanced methods from random matrix theory and quantum chemistry. The derivation suggests new mathematical preconditions for ideal learning, including a new metric, ERG, which is equivalent to applying a single step of the Wilson Exact Renormalization Group. We test the assumptions and predictions of SETOL on a simple 3-layer multilayer perceptron (MLP), demonstrating excellent agreement with the key theoretical assumptions. For SOTA NN models, we show how to estimate the individual layer qualities of a trained NN by simply computing the empirical spectral density (ESD) of the layer weight matrices and plugging this ESD into our SETOL formulas. Notably, we examine the performance of the HTSR alpha and the SETOL ERG layer quality metrics, and find that they align remarkably well, both on our MLP and on SOTA NNs.

• The paper presents a novel semi-empirical framework linking heavy-tailed spectral metrics with ideal learning conditions in deep neural networks.
• It employs the HCIZ integral to derive a Layer Quality metric that explains how an optimal PL exponent (α ≈ 2) predicts generalization performance.
• Empirical validations across MLPs and state-of-the-art models confirm the alignment of HTSR and TRACE-LOG conditions for robust model regularization.

SETOL: A Semi-Empirical Theory of (Deep) Learning

SETOL introduces a semi-empirical theoretical framework for understanding and predicting the generalization properties of deep neural networks (DNNs), unifying concepts from statistical mechanics, heavy-tailed random matrix theory (HT-RMT), and empirical observations of modern neural architectures. The theory provides a formal derivation and justification for the widely used Heavy-Tailed Self-Regularization (HTSR) metrics—specifically, the Power Law (PL) exponents Alpha ($\alpha$) and AlphaHat ($\hat{\alpha}$)—and introduces the TRACE-LOG condition as a new, independent criterion for ideal learning. SETOL is constructed as a matrix generalization of the Student-Teacher (ST) model, with the teacher taken as empirical input, and leverages the Harish-Chandra–Itzykson–Zuber (HCIZ) integral to connect empirical spectral densities (ESDs) of layer weight matrices to theoretical predictions.

---

Theoretical Foundations: From HTSR Phenomenology to SETOL

HTSR theory empirically established that well-trained DNN layers exhibit heavy-tailed ESDs, with the tail well-fit by a power law $\rho(\lambda) \sim \lambda^{-\alpha}$, and that the PL exponent $\alpha$ robustly predicts generalization performance across architectures and domains. The critical value $\alpha=2$ demarcates a phase boundary: layers with $\alpha \approx 2$ are optimally regularized, while $\alpha < 2$ indicates over-regularization and potential overfitting.

SETOL provides a first-principles derivation of these empirical findings. It models each layer as a matrix-generalized ST system, where the generalization accuracy is determined by the overlap between a fixed teacher (the trained layer) and an ensemble of students (random matrices with similar spectral properties). The central object is the Layer Quality (squared), $\mathcal{Q}^2$, defined as a thermal average over the squared overlap, which is evaluated as an HCIZ integral in the large-$N$ limit.

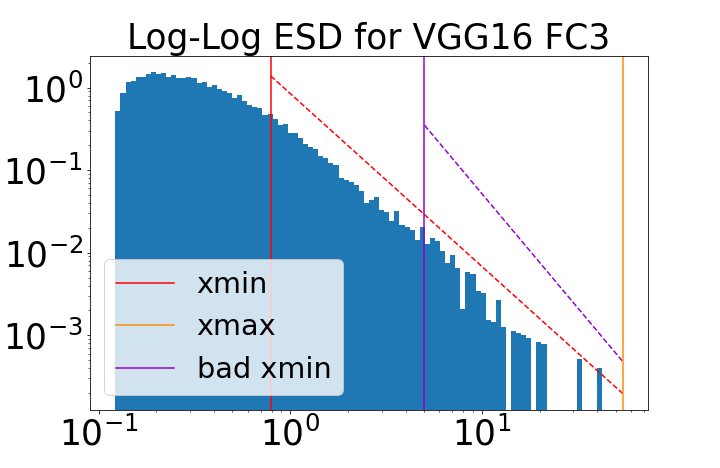
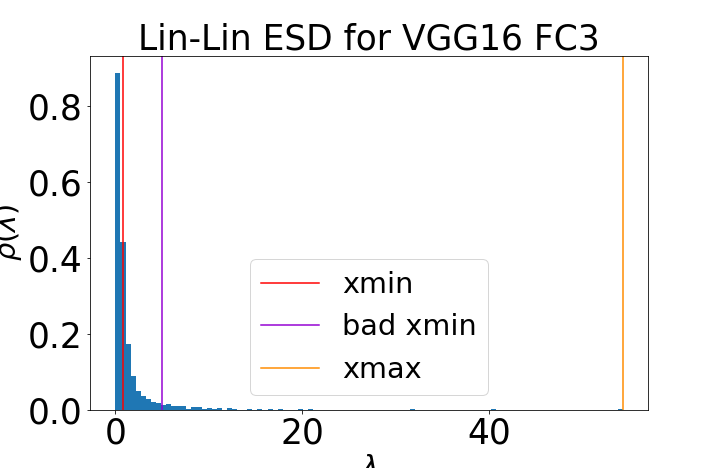
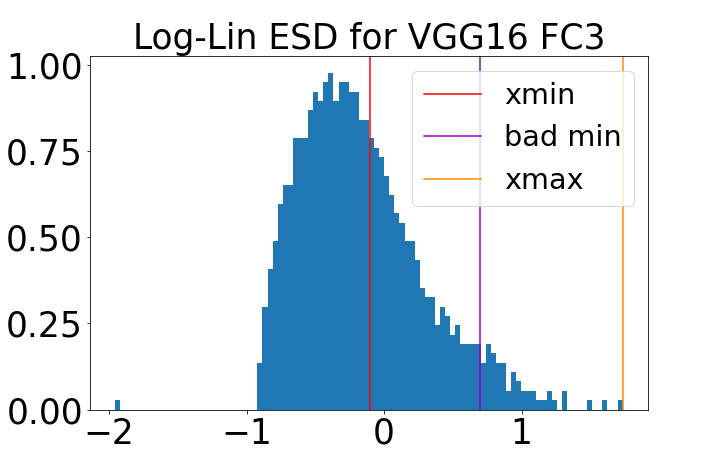
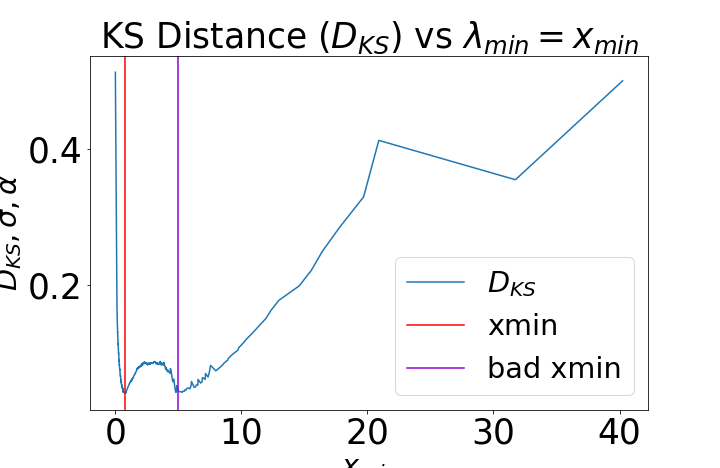
Figure 1: Fitting ESDs within HTSR. The ESD of a well-trained VGG19 layer is shown with both good (red) and bad (purple) PL fits, highlighting the importance of accurate tail selection for $\alpha$ estimation.

The SETOL framework introduces two key mathematical conditions for ideal learning:

• HTSR Condition: The ESD tail is well-fit by a PL with $\alpha \approx 2$.
• TRACE-LOG Condition: The product of the dominant eigenvalues in the effective correlation space (ECS) satisfies $\prod_i \lambda_i = 1$, or equivalently, $\sum_i \ln \lambda_i = 0$.

These conditions are shown to be empirically aligned in both simple MLPs and large-scale pretrained models.

---

Matrix Generalization and the Effective Correlation Space

SETOL's matrix generalization replaces the vector overlap of classical ST models with a trace over the product of student and teacher correlation matrices. The theory posits that generalization-relevant information is concentrated in a low-rank ECS, defined by the tail of the ESD. The HCIZ integral, evaluated in the ECS, yields the Layer Quality as a sum over integrated R-transforms of the ESD:

$$\mathcal{Q}^2 = \sum_{i=1}^M G(\lambda_i) = \sum_{i=1}^M \int_{\lambda_{\text{min}}}^{\lambda_i} R(z) dz$$

where $R(z)$ is the R-transform associated with the ESD, and $\lambda_{\text{min}}$ is the ECS cutoff, determined either by the PL fit or the TRACE-LOG condition.

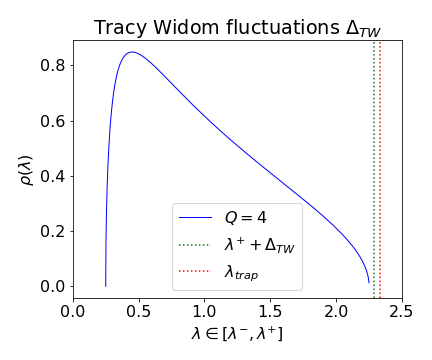
Figure 2: MP distributions for different aspect ratios $Q$ and variance scales $\sigma^2$, and an example of the finite-sized TW fluctuation $\Delta_{TW}$.

The choice of $R(z)$ models (e.g., Free Cauchy, Inverse Marchenko-Pastur, Lévy-Wigner) allows SETOL to recover the empirical Alpha and AlphaHat metrics as leading-order approximations, and to extend the analysis to non-ideal, overfit, or underfit regimes.

---

Empirical Validation: MLP3 and SOTA Models

SETOL's predictions are validated on a three-layer MLP (MLP3) trained on MNIST, as well as on large-scale pretrained models (VGG, ResNet, ViT, DenseNet, Llama, Falcon). Key findings include:

• Alpha and Generalization: As batch size decreases or learning rate increases, $\alpha$ in the dominant layer approaches 2, coinciding with minimal test error. Further reduction leads to $\alpha < 2$, increased error, and larger error variance, indicating over-regularization.

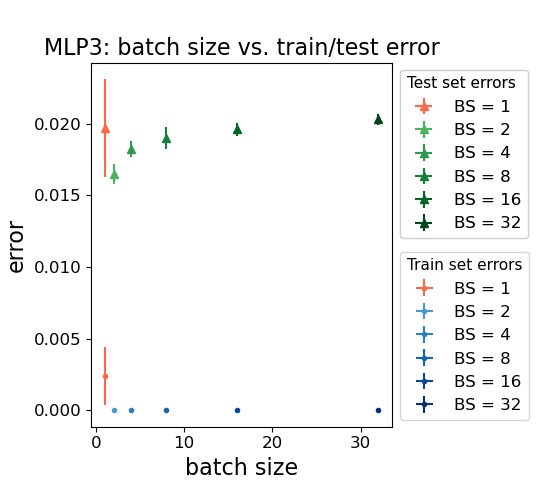
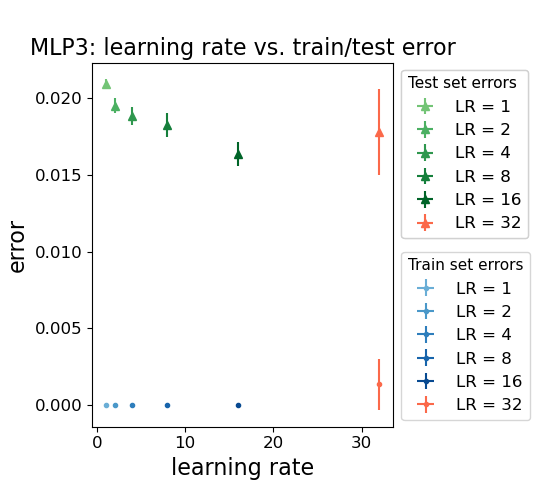
Figure 4: Train/test errors in the MLP3 model as a function of batch size and learning rate. Test error decreases as batch size decreases or learning rate increases, until a critical point where overfitting occurs.

• TRACE-LOG Alignment: The ECS cutoff determined by the TRACE-LOG condition converges to the PL tail cutoff as $\alpha \to 2$. The difference $$\Delta \lambda_{\text{min}} = \lambda_{\text{PL}} - \lambda_{\text{TRACE-LOG}}$$ approaches zero at this critical point.

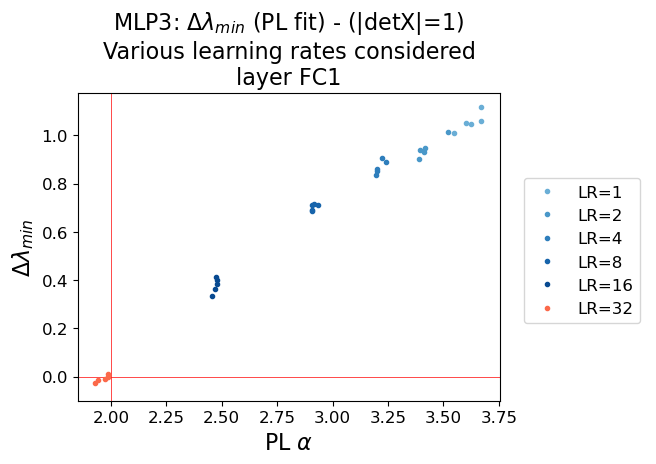
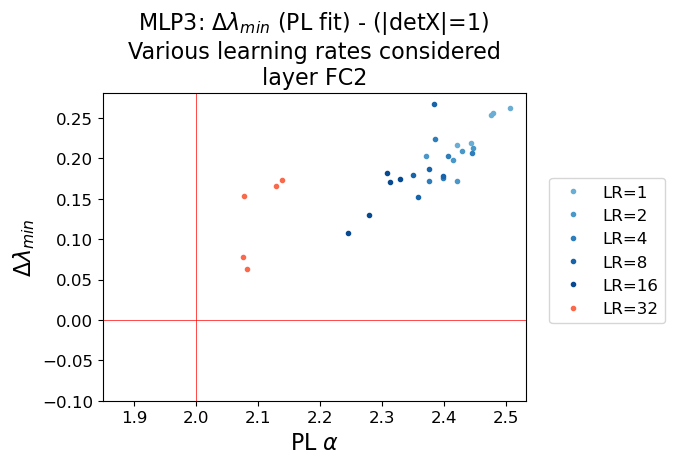
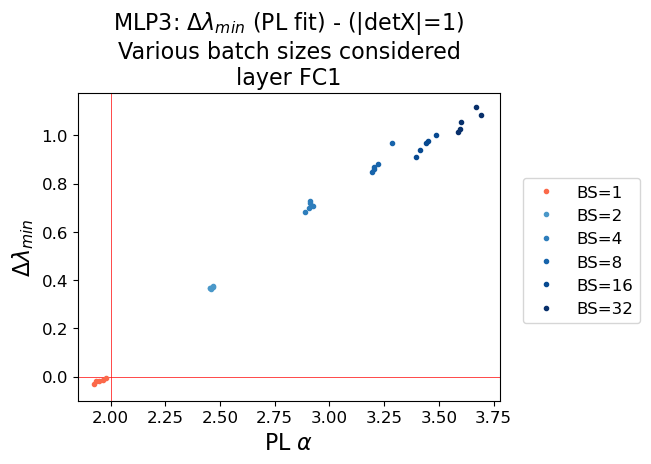
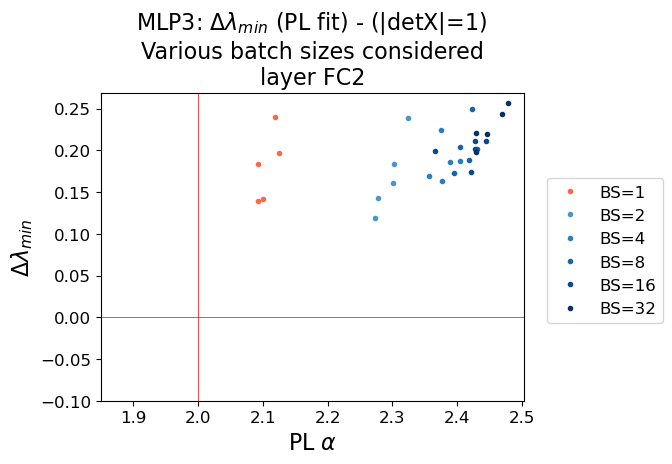
Figure 6: MLP3 Model: Comparison of the PL Alpha (x-axis), with the difference between PL and TRACE-LOG cutoffs (y-axis). The critical point $(\alpha=2, \Delta\lambda_{\text{min}}=0)$ marks the transition to ideal learning.

• Correlation Traps: Excessively large learning rates or small batch sizes induce correlation traps—large, spurious eigenvalues in the randomized ESD—leading to $\alpha < 2$ and degraded generalization.

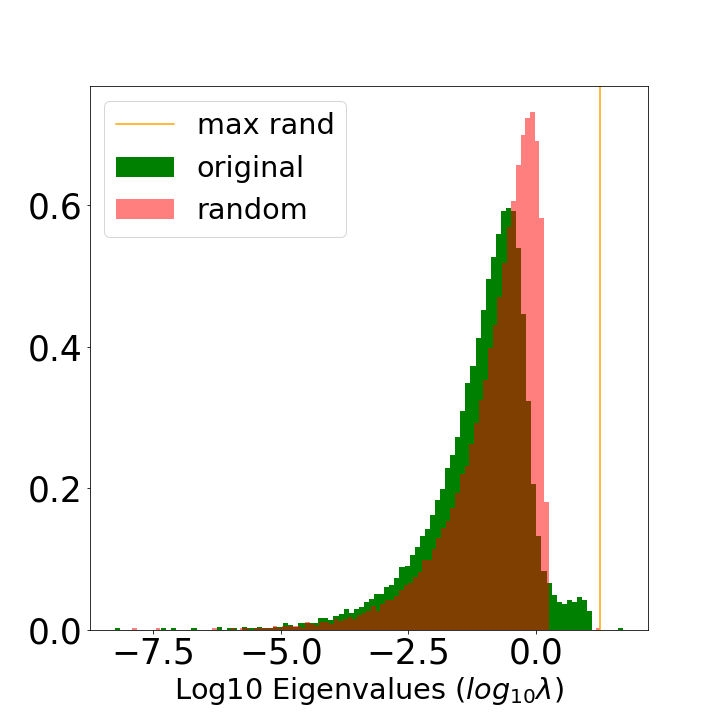
Figure 7: Comparison of a well-formed, Heavy-Tailed ESD (a) to one with a Correlation Trap (b), in the VGG16 model (FC2 layer).

• SOTA Models: In VGG, ResNet, ViT, DenseNet, and LLMs, the majority of layers cluster near $(\alpha=2, \Delta\lambda_{\text{min}}=0)$, with deviations indicating under- or over-regularization.

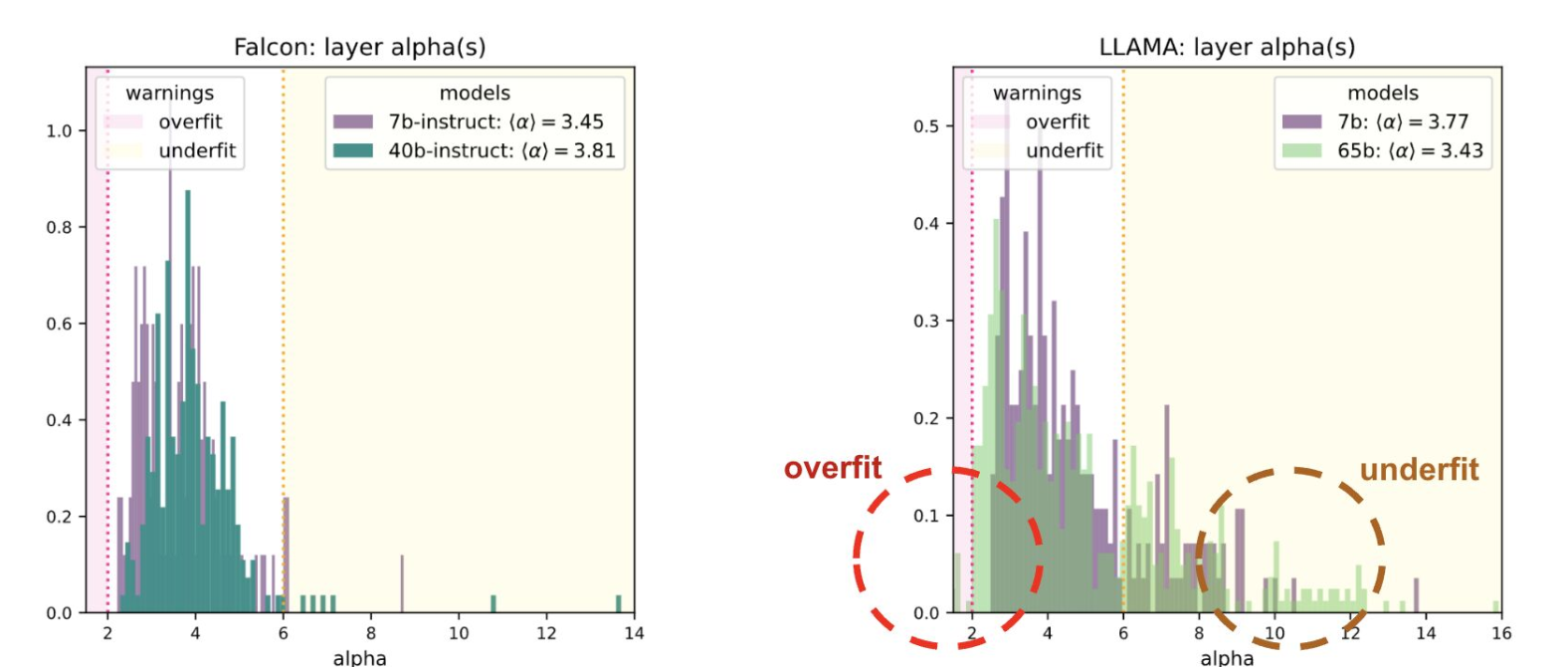
  Figure 8: Falcon vs Llama. Layerwise Alpha metrics for Falcon-40b and Llama-65b. Falcon layers cluster in the optimal $\alpha\in[2,6]$ range, while Llama exhibits both underfit ($\alpha>6$) and overfit ($\alpha<2$) layers.

---

Computational R-Transform Metrics and Scaling

SETOL enables direct computation of layer quality via the R-transform and its cumulant expansion, providing a principled alternative to empirical PL fits. In practice, the computational R-transform metric $\mathcal{Q}$ tracks $\alpha$ closely in dominant layers, but exhibits higher variance in smaller or less critical layers.

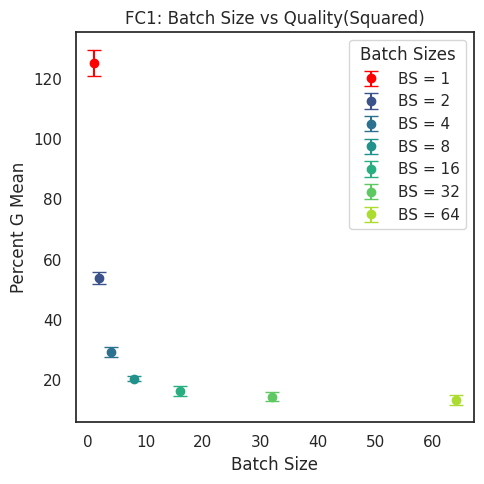
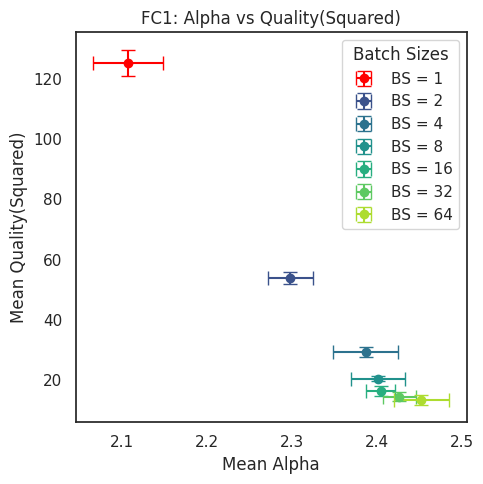
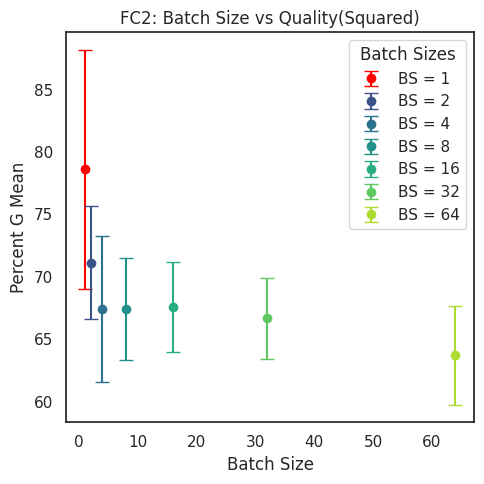
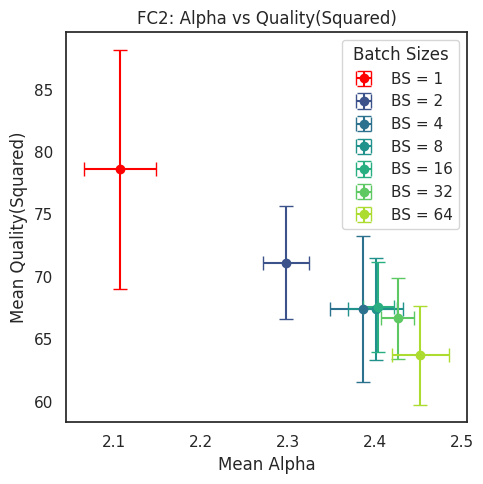
Figure 10: Evaluation of the computational R-transform LayerQualitySquared metric $\mathcal{Q}$ on the fully trained MLP3 model(s) for different batch sizes.

Scaling considerations are addressed via the normalization of weight matrices and the restriction to the ECS, ensuring that SETOL metrics remain size-consistent and intensive in the thermodynamic limit.

---

Implications, Limitations, and Future Directions

SETOL provides a rigorous, data-free framework for diagnosing and predicting generalization in deep networks, with immediate applications to model selection, fine-tuning, pruning, and compression. The alignment of the HTSR and TRACE-LOG conditions offers a robust criterion for identifying optimally regularized layers, while deviations signal overfitting, underfitting, or the presence of correlation traps.

Limitations:

• SETOL is fundamentally a single-layer theory; inter-layer interactions and cross-terms are not explicitly modeled.
• The theory assumes the existence of a well-defined ECS and may be less effective in underparameterized or highly non-ideal regimes.
• The independence assumption (IFA) between terms in the HCIZ integral is a mathematical convenience, not always empirically justified.

Future Directions:

• Extension to multi-layer ERG and explicit modeling of layer-layer interactions.
• Integration of SETOL diagnostics into training and fine-tuning pipelines for large-scale models.
• Systematic paper of correlation traps, meta-stable states, and the role of the layer null space.
• Development of more accurate R-transform models for non-ideal ESDs and exploration of connections to spin glass theory and quantum many-body systems.

---

Conclusion

SETOL unifies empirical observations and theoretical modeling of deep learning generalization, providing a principled explanation for the predictive power of heavy-tailed spectral metrics and introducing the TRACE-LOG condition as a new, independent criterion for ideal learning. The framework bridges statistical mechanics, random matrix theory, and practical diagnostics, offering both a conceptual advance and actionable tools for the analysis and optimization of modern neural networks. The alignment of the HTSR and TRACE-LOG conditions at $\alpha=2$ marks a critical point of optimal generalization, with broad implications for the design, training, and evaluation of deep learning systems.