Bayesian Triplet Loss: Uncertainty Quantification in Image Retrieval (2011.12663v3)

Abstract: Uncertainty quantification in image retrieval is crucial for downstream decisions, yet it remains a challenging and largely unexplored problem. Current methods for estimating uncertainties are poorly calibrated, computationally expensive, or based on heuristics. We present a new method that views image embeddings as stochastic features rather than deterministic features. Our two main contributions are (1) a likelihood that matches the triplet constraint and that evaluates the probability of an anchor being closer to a positive than a negative; and (2) a prior over the feature space that justifies the conventional l2 normalization. To ensure computational efficiency, we derive a variational approximation of the posterior, called the Bayesian triplet loss, that produces state-of-the-art uncertainty estimates and matches the predictive performance of current state-of-the-art methods.

• The paper introduces Bayesian Triplet Loss, incorporating uncertainty quantification in image retrieval by modeling embeddings as stochastic distributions.
• It replaces traditional deterministic triplet loss with a probabilistic framework using Gaussian approximations to efficiently compute mean and variance of embeddings.
• Experimental results on datasets like CUB 200-2011 confirm enhanced calibration and improved out-of-distribution detection, bolstering decision-making in critical applications.

Bayesian Triplet Loss: Uncertainty Quantification in Image Retrieval

Introduction

The paper investigates the use of Bayesian modeling to enhance uncertainty quantification in image retrieval tasks, proposing a method that treats image embeddings as stochastic features. Traditional methods often rely on deterministic embeddings, which lack a mechanism for expressing confidence in the retrieval process. By modeling embeddings as distributions, this approach aims to provide robust uncertainty estimates alongside predictions, improving decision-making in critical applications.

Method Overview

The key innovation in this work is the introduction of the Bayesian Triplet Loss, designed to replace deterministic triplet loss functions. This formulation employs a likelihood that matches the triplet constraint, evaluating the probability that an anchor image is closer to a positive sample than a negative. Further, the approach utilizes a prior over the feature space, justifying conventional $\ell_2$ normalization and facilitating the Bayesian inference process.

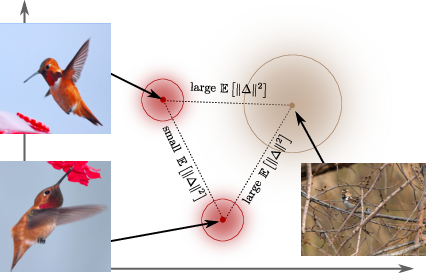
Figure 1: We model embeddings as distributions rather than point estimates, such that data uncertainty is propagated to retrieval. We phrase a Bayesian model that mirrors the triplet loss, which enables us to learn stochastic features.

Bayesian Triplet Loss Mechanism

The Bayesian Triplet Loss is derived from a probability expression that extends the traditional triplet formulation. This expression, considered as a multinomial distribution, assesses the likelihood of hypotheses about relative positions of sample triplets in the spatial embedding space.

In implementing this approach, the paper details the necessary steps to determine the mean and variance of the embedding distances involved. By leveraging the Central Limit Theorem, the complex distribution of triplet distances is approximated as Gaussian, leading to computationally efficient uncertainty estimates.

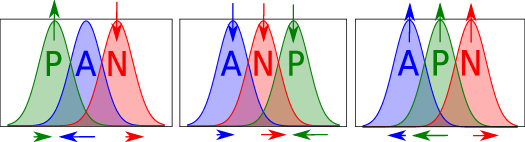
Figure 2: Intuition for the Bayesian triplet loss in three 1D scenarios. The arrows indicate gradient directions with respect to means and variances.

Network Architecture

The architecture employed includes a backbone CNN for feature extraction, coupled with dual branches to estimate mean and variance of the embeddings. A modified Generalized Mean (GeM) pooling followed by fully connected layers computes the mean embedding, while a separate set of layers computes the variance, incorporating a softplus activation to ensure positivity.

Figure 3: Overview of our network architecture.

Experimental Evaluation

Experiments conducted across diverse datasets, such as CUB 200-2011 and MSLS, demonstrate the model's efficacy. The Bayesian framework not only matches traditional methods in predictive performance but also excels in generating well-calibrated uncertainty measures. This is confirmed through metrics like Expected Calibration Error (ECE), which quantifies alignment between predicted probabilities and observed frequencies, indicating improved model reliability.

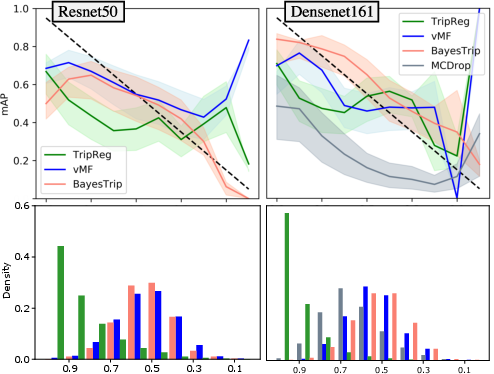
Figure 4: Calibration plots showing how the Bayesian triplet loss with Gaussian embeddings yields better calibration than alternatives like MC dropout.

Implications and Future Work

The provision of uncertainty estimates aims to enhance various downstream applications, from autonomous systems requiring risk assessment to user-centric retrieval systems demanding reliability and interpretability. Practical implications include the fine-tuning of retrieval pipelines to prioritize high-confidence predictions and the seamless integration of OOD detection.

Figure 5: Histogram demonstrating the separation of covariance in distances between in-distribution and out-of-distribution queries, highlighting improved OOD detection capabilities.

Future research directions might explore expanded uses of these uncertainty estimates, potentially incorporating them into training pipelines as a feedback mechanism to focus learning on more ambiguous or complex regions of data space.

Conclusion

The Bayesian Triplet Loss advances the field of image retrieval by embedding uncertainty quantification directly into the retrieval process. This dual emphasis on accuracy and uncertainty offers substantial benefits, particularly in applications where reliability is paramount. While current implementations demonstrate significant promise, ongoing research will continue to refine and expand these methodologies, further embedding uncertainty as a cornerstone of AI capabilities.