Spectral Collapse: Theory & Applications

Updated 13 December 2025

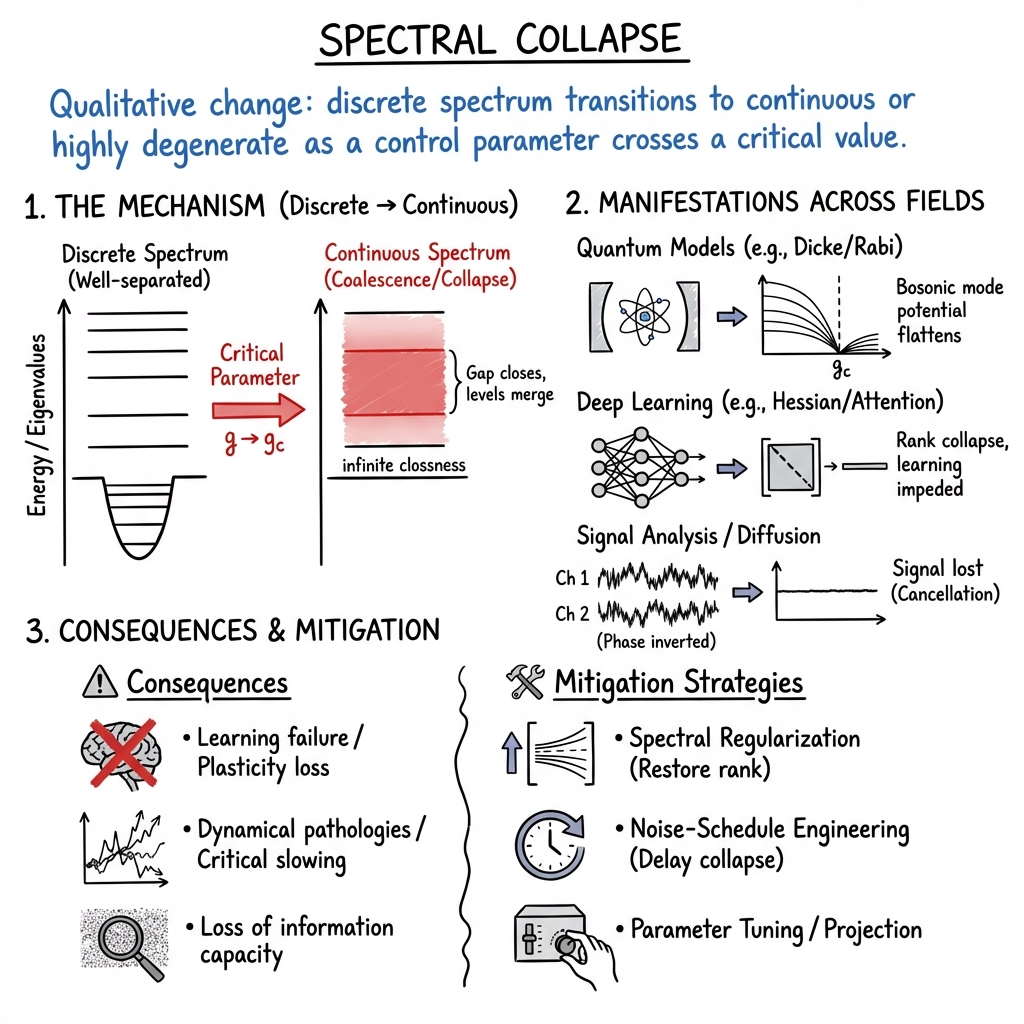
Spectral collapse is defined as a transition from discrete eigenmodes to a continuous or degenerate spectrum when a control parameter exceeds a critical threshold, affecting quantum, optical, and neural systems.
It manifests experimentally through observable phenomena such as fluorescence line coalescence, vanishing normal modes in Bose-Hubbard models, and rank collapse in neural network Hessians.
Mitigation strategies including spectral regularization, noise-schedule engineering, and tailored phase corrections are crucial for stabilizing systems and preserving effective information processing.

Spectral collapse denotes a qualitative change in the spectral properties of a linear operator (or matrix, or Liouvillian superoperator) when a control parameter crosses a critical value, typically manifesting as a transition from a discrete (pure-point) spectrum to a continuous spectrum, or as an abrupt degeneracy of eigenvalues. Originally identified in quantum models with nonlinear interactions, the term now encompasses a range of phenomena across quantum optics, condensed matter, nonlinear waves, neural networks, signal analysis, and even noncommutative geometry. While the underlying mechanisms differ by context, spectral collapse universally signals the loss of distinct energy levels, modes, or directions, often leading to dynamical pathologies, critical phenomena, or breakdowns in information processing.

1. Theoretical Foundations and Definitions

Spectral collapse arises in systems where the spectrum of an operator or matrix, initially composed of well-separated (discrete) eigenvalues, undergoes a coalescence into a continuous band or develops highly degenerate points as a critical parameter is varied. In quantum models, this is exemplified by the two-photon Rabi or Dicke Hamiltonians, where the bosonic mode transitions from a bounded (oscillator-like) potential to a flat or inverted potential as the nonlinear coupling approaches a critical value, leading to spectral collapse at that threshold (Felicetti et al., 2019, Duan et al., 2016, Felicetti et al., 2015, Rico et al., 2019).

The phenomenon also appears in:

Two-species Bose-Hubbard dimers: As the interspecies coupling reaches a threshold, the normal-mode frequencies vanish, and the discrete low-lying spectrum becomes continuous, reflecting a dynamical change in the underlying algebra (Lingua et al., 2016).
Open quantum systems: In the Scully–Lamb laser model, Liouvillian spectral collapse refers to the coalescence of infinitely many decay rates ("Liouvillian eigenvalues") at a dissipative phase transition—producing diabolic points of infinite degeneracy (Minganti et al., 2021).
Deep neural networks: Hessian spectral collapse describes the vanishing of positive eigenvalues in the loss Hessian at new-task initialization, curtailing gradient descent and learning ("plasticity loss") (He et al., 26 Sep 2025).
Attention mechanisms in transformers: Spectral collapse manifests as a sharp gap between the leading singular value and the remaining spectrum, causing rank collapse in width and in depth, which impedes gradient flow and expressivity (Saada et al., 10 Oct 2024).
Score-based diffusion models: In turbulence emulation, spectral collapse refers to the destruction of high-wavenumber signal-to-noise ratio due to inappropriate noise schedules, precluding the model from capturing multiscale dynamics (Sambamurthy et al., 10 Dec 2025).
Noncommutative geometry: Spectral triples may experience spectral collapse as one component of the Dirac operator is rescaled to zero, corresponding to geometric "collapse," with operator spectra converging in a well-defined topology (Farsi et al., 30 Mar 2024).
Cross-spectral analysis: Under special phase-inversion configurations, cross-spectral density can vanish over large bands, nulling the detection of target signals (cross-spectral collapse) (Nelson et al., 2013).
GANs: Spectral collapse in the discriminator corresponds to the majority of singular values of the weight matrices falling to zero, tightly linked to mode collapse in the generator (Liu et al., 2019).

2. Key Mechanisms and Mathematical Criteria

The mathematical mechanism underlying spectral collapse is system-dependent but shares certain features:

System	Control Parameter	Collapse Criterion	Spectral Change
Two-photon Dicke/Rabi	$g_2$ , $g$	$g_c = \omega/(4N)$ (Dicke), $g_c = \omega/2$ (Rabi)	Discrete $\rightarrow$ Continuous, spectrum unbounded above $g_c$
Bose-Hubbard dimer	$W$	$W_c^2 = U_a U_b$	Vibrational branch gap closes, continuous spectrum
Scully–Lamb Liouvillian	Pump $A$	$A_c = \Gamma$	Infinite degeneracy, decay rates coalesce to zero
Neural network Hessian	Task accumulation	min positive $\lambda_i \rightarrow 0$	Rank loss, learning failure
Attention matrices	Context length $T$	$T \to \infty$ , gap $\Delta \sim 1$	Rank collapse, bulk spectrum vanishes
Diffusion models	Diffusion time $t$	SNR $(k,t) \downarrow$ at high $k$	Signal lost at high frequencies
Cross-spectrum	Phase flip, $S_c=S_d$	Phase inversion, matched PSDs	Cross-spectrum vanishes

In multi-mode quantum settings, the effective potential governing bosonic modes becomes flat or inverted at critical coupling, causing the spatial eigenstates to delocalize and the eigenvalue spacing to vanish (Felicetti et al., 2019, Felicetti et al., 2015). In signal analysis, phase inversion in one channel and matching of power spectra leads to algebraic cancellation of the target signal (Nelson et al., 2013). In high-dimensional neural architectures, the spectrum of random matrices or layer Hessians contracts to rank-one or loses positive curvature, respectively (Saada et al., 10 Oct 2024, He et al., 26 Sep 2025).

3. Physical Realizations and Observables

Multiple physical systems admit experimental or computational observation of spectral collapse phenomena:

Circuit QED and Trapped Ions: Realization of the two-photon Dicke or Rabi model via superconducting flux qubits coupled to microwave resonators, with the quadratic $\sigma_x(a+a^\dagger)^2$ interaction engineered by circuit design, or via bichromatic driving of trapped ions on the second red/blue sidebands. Observable signatures include (i) the coalescence and compression of fluorescence lines in spectroscopic measurement as $g_2\to g_c$ , and (ii) the divergence of field quadratures or phonon number at collapse (Felicetti et al., 2019, Felicetti et al., 2015).
Scattering and Spectroscopy: Spectral collapse is directly detected via inelastic scattering (fluorescence) spectra that exhibit a sharp proliferation and red-shift of lines as collapse is approached (Felicetti et al., 2019).
Wave turbulence simulations: Forced-dissipated nonlinear PDEs (e.g., MMT equation) show a transition from power-law to exponential spectra as collapse turbulence dominates, associated with intermittent, high-amplitude events and statistical changes in field statistics (Simonis et al., 28 Feb 2024).
Deep learning and GANs: Discriminator spectral collapse is captured by monitoring the spectrum of weight matrices during training; a rapid decay of all but the largest singular values coincides with mode collapse and degraded generator performance (Liu et al., 2019).

4. Dynamical, Algebraic, and Critical Properties

Spectral collapse is intertwined with dynamical and algebraic properties:

Dynamical Algebra Transitions: The underlying dynamical algebra may change as the collapse threshold is crossed (e.g., from SU(2) $\times$ SU(1,1) to independent Heisenberg–Weyl algebras in Bose–Hubbard dimers) (Lingua et al., 2016).
Non-perturbative Nature: The gap between ground and excited states at collapse is nonperturbative and invisible to any finite-order expansion; variational or exact treatments are required (Duan et al., 2016).
Critical Dynamics: In open systems, collapse is associated with critical slowing-down, multistability, and emergence of anomalous dynamical features (e.g., bistability enabled by quantum fluctuations) (Minganti et al., 2021).
Signal/Gradient Pathologies: In neural settings, spectral collapse precipitates ill-conditioned loss landscapes (in continual learning) or vanishing/exploding gradients and loss of representation diversity (in transformers) (He et al., 26 Sep 2025, Saada et al., 10 Oct 2024).

5. Practical Consequences and Mitigation Strategies

Spectral collapse typically induces unfavorable or pathological behaviors in physical and computational systems. Various mitigation strategies have been introduced:

Spectral Regularization in GANs: Actively correcting tail singular values of weight matrices in the discriminator prevents spectral collapse, thus staving off mode collapse in the generator. Static or dynamic compensation schemes restore the full spectrum and stabilize training (Liu et al., 2019).
Spectral Correction in Attention: Projecting out the rank-one uniform vector from attention matrices at each layer eliminates the spectral gap and capacitated rank collapse, improving gradient propagation and expressivity (Saada et al., 10 Oct 2024).
Regularization in Continual Learning: Adding effective feature-rank penalties and $L^2$ weight decay preserves Hessian spectrum rank and positive curvature, maintaining trainability over many tasks (He et al., 26 Sep 2025).
Noise-Schedule Engineering in Diffusion Models: Power-law noise schedules, delaying forward SNR collapse at high modes, enable physically faithful multiscale learning in turbulent flow emulation. One-step Lazy Diffusion distillation further preserves spectral fidelity (Sambamurthy et al., 10 Dec 2025).
Signal Analysis Diagnostics: For cross-spectral analysis, ensuring that both channels are aligned in phase for all noise sources, actively controlling conversion quadrants, or designing robust diagnostic sweeps guards against hidden spectral collapse (Nelson et al., 2013).

6. Universality and Generalizations

Spectral collapse represents a universal marker of a major algebraic (commutant, parity, symmetry), topological, or dynamical transition in a system's operator structure. It may signal:

Finite-to-infinite degeneracy transitions: Critical points where discrete state multiplicities become infinite.
Gap closings: Onset of continuous spectra in many-body or field models, and phase transitions in open quantum systems.
Loss of information-carrying capacity: Collapse of signal-to-noise in statistical or neural models, or the flattening of operators in noncommutative geometry as one component "collapses" (e.g., via rescaling, quotient, or limit).
Critical phenomena simulability: In optical lattices or mesoscopic systems, spectral collapse can be used as a controllable probe of critical behavior and correlated regimes (Lingua et al., 2016, Felicetti et al., 2019).

The mathematical framework underpinning spectral collapse now appears in settings ranging from functional analytic operator theory (spectral triples), semiclassical and quantum phase transitions, machine learning, and even experimental time-series analysis. Its relevance is expected to grow as new platforms access regimes of strong coupling, high parameter count, or complex stochasticity.