Sinkhorn–Knopp Algorithm

• The Sinkhorn–Knopp algorithm is an iterative method that alternates row and column normalization to transform a matrix into a doubly stochastic one.
• It leverages the geometric and combinatorial properties of the Birkhoff polytope, ensuring unique convergence under proper conditions.
• Recent advancements use acceleration techniques like overrelaxation and Krylov subspace methods to improve convergence, especially in low-entropy settings.

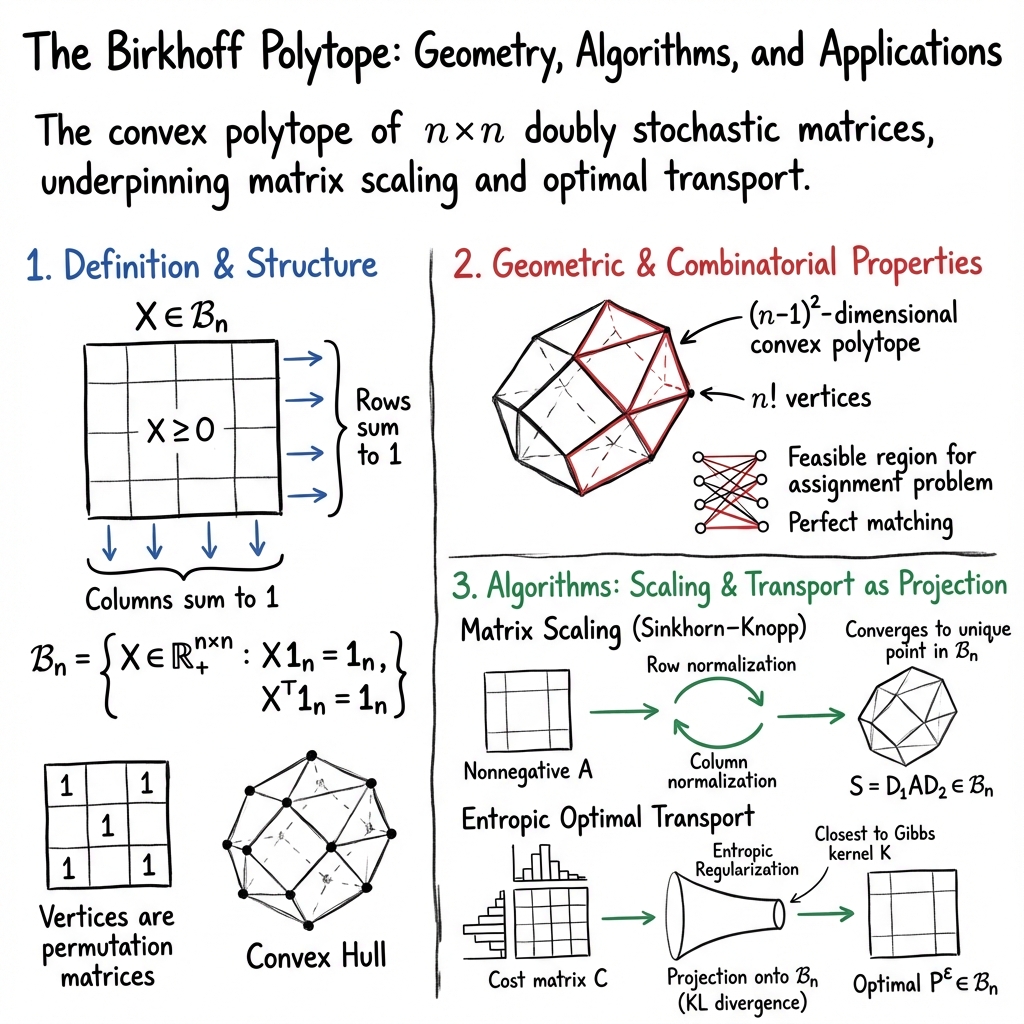
The Birkhoff polytope is the convex polytope of $n \times n$ doubly stochastic matrices. It arises as the feasible region for matrix scaling and entropic optimal transport, and serves as the canonical set of couplings in discrete transport problems. The vertices of the Birkhoff polytope are precisely the $n \times n$ permutation matrices, and its geometry underpins a variety of algorithms—including the Sinkhorn–Knopp procedure—for matrix balancing, optimal transport, and more. The Birkhoff polytope’s structure, its connections to combinatorics, and its algorithmic role in optimization are central in both theoretical and applied domains.

1. Definition and Polytope Structure

The Birkhoff polytope $\mathcal{B}_n$ is the set of all $n\times n$ doubly stochastic matrices: $$\mathcal{B}_n = \left\{ X \in \mathbb{R}_+^{n \times n} : X \mathbf{1}_n = \mathbf{1}_n,\, X^\top \mathbf{1}_n = \mathbf{1}_n \right\}$$ where $\mathbf{1}_n$ is the all-ones column vector. A matrix $X \in \mathcal{B}_n$ has nonnegative entries, and each row and column sums to one.

The Birkhoff–von Neumann theorem asserts that $\mathcal{B}_n$ is the convex hull of the set of $n \times n$ permutation matrices. Therefore, every doubly stochastic matrix can be expressed as a convex combination of permutation matrices.

2. Geometric and Combinatorial Properties

The Birkhoff polytope is a $(n-1)^2$-dimensional convex polytope with $n!$ vertices, corresponding to the $n!$ possible permutation matrices of size $n \times n$ (Modin, 2023). Its faces, edges, and extreme points encode combinatorial structures such as matchings and assignments. The polytope is centrally symmetric and highly structured, with tight control over marginal constraints.

From a combinatorial optimization perspective, $\mathcal{B}_n$ serves as the feasible region for the assignment problem and the max-weight perfect matching problem. Its facial structure is exploited by algorithms in combinatorial optimization and by theoretical analyses using polytope theory.

3. Birkhoff Polytope as the Feasible Set in Matrix Scaling

The fundamental problem of matrix scaling seeks diagonal matrices $D_1$, $D_2$ such that $S = D_1 A D_2$ is doubly stochastic, i.e., $S \in \mathcal{B}_n$ for a nonnegative $A$ with total support (Mazzilli et al., 2022). The Sinkhorn–Knopp algorithm alternately normalizes rows and columns, iteratively projecting onto the affine constraints defined by the Birkhoff polytope. These iterations converge to a unique point in $\mathcal{B}_n$ closest to $A$ in relative entropy (KL divergence), provided the initial $A$ is positive or supported appropriately.

Scaling matrices to achieve prescribed marginals is therefore equivalent to projecting onto $\mathcal{B}_n$ in an appropriate metric geometry (typically KL/Bregman). This characterization is central to discrete optimal transport, preconditioning, and normalization schemes.

4. Optimal Transport and Entropic Regularization

Discrete optimal transport problems: $$\min_{P \geq 0} \langle P, C \rangle \quad \text{subject to } P \mathbf{1}_n = a,\, P^\top \mathbf{1}_n = b$$ seek couplings $P$ in $\mathcal{B}_n$ when $a, b = \mathbf{1}_n$. Entropic regularization smooths the classical transport problem: $$\min_{P \in \mathcal{B}_n} \langle P, C \rangle + \varepsilon \sum_{i,j} P_{ij} \log P_{ij}$$ This remains a projection onto the Birkhoff polytope in the sense of KL geometry. The optimal $P^\varepsilon$ is of form $$P^\varepsilon = \mathrm{diag}(u)\, K\, \mathrm{diag}(v)$$, with $K$ the Gibbs kernel and $(u,v)$ chosen such that $P^\varepsilon \in \mathcal{B}_n$ (Cuturi, 2013). The solution corresponds to a point in the polytope closest to $K$ (or the cost-encoded matrix) with margins enforced.

5. Algorithmic Approaches: Sinkhorn–Knopp and Acceleration

The iterative matrix scaling algorithms operate as alternating projections onto the row and column sums defining $\mathcal{B}_n$. The Sinkhorn–Knopp algorithm applies the updates: $$u^{(t+1)} = \mathbf{1}_n \mathbin{/} (K v^{(t)}),\quad v^{(t+1)} = \mathbf{1}_n \mathbin{/} (K^\top u^{(t+1)})$$ resulting in exponential convergence to the balanced solution in $\mathcal{B}_n$ (Ali et al., 2024).

Recent advances involve reformulating the scaling problem as a nonlinear multiparameter eigenvalue problem on the polytope, and using Arnoldi/Krylov subspace methods for accelerated computation in regimes where the Birkhoff polytope’s spectral structure induces slow convergence by basic alternation (Aristodemo et al., 2018). Overrelaxation techniques further leverage the geometric structure of $\mathcal{B}_n$ to reduce iteration count in low-entropy settings (1711.01851).

6. Complexity, Phase Transitions, and Structural Limits

For a square $n \times n$ matrix with normalized density $\gamma$, the Sinkhorn–Knopp algorithm achieves nearly doubly-stochastic scaling in $O(\log n - \log \varepsilon)$ iterations and $\widetilde O(n^2)$ total time for matrices whose normalized version is $\gamma$-dense with $\gamma > 1/2$. The Birkhoff polytope’s intrinsic geometry enables this optimal complexity; matrices with $\gamma < 1/2$ density cause a sharp phase transition to polynomial iteration bounds (He, 13 Jul 2025). The exponential contraction in the polytope’s projective geometry underpins efficient balancing in practical settings.

7. Extensions: Quantum, Constrained, and Stochastic Variants

Generalizations of the Birkhoff polytope appear in quantum circuit decomposition (unitary matrices scaled to unit line-sums over $\mathbb{C}$), constrained optimal transport with prescribed zero-entries in the plan (faces or slices of $\mathcal{B}_n$; see (Corless et al., 2024)), and in mirror-descent interpretations where projection onto multiple marginal polytopes recovers higher-order assignment problems (Mishchenko, 2019).

The Birkhoff polytope’s rich geometric, combinatorial, and algorithmic structure establishes it as a foundational object in the theory and practice of matrix balancing, optimal transport, and high-dimensional scaling. Its role is central in convergence analysis, algorithm design, and in the deeper geometric understanding of doubly-stochastic couplings.