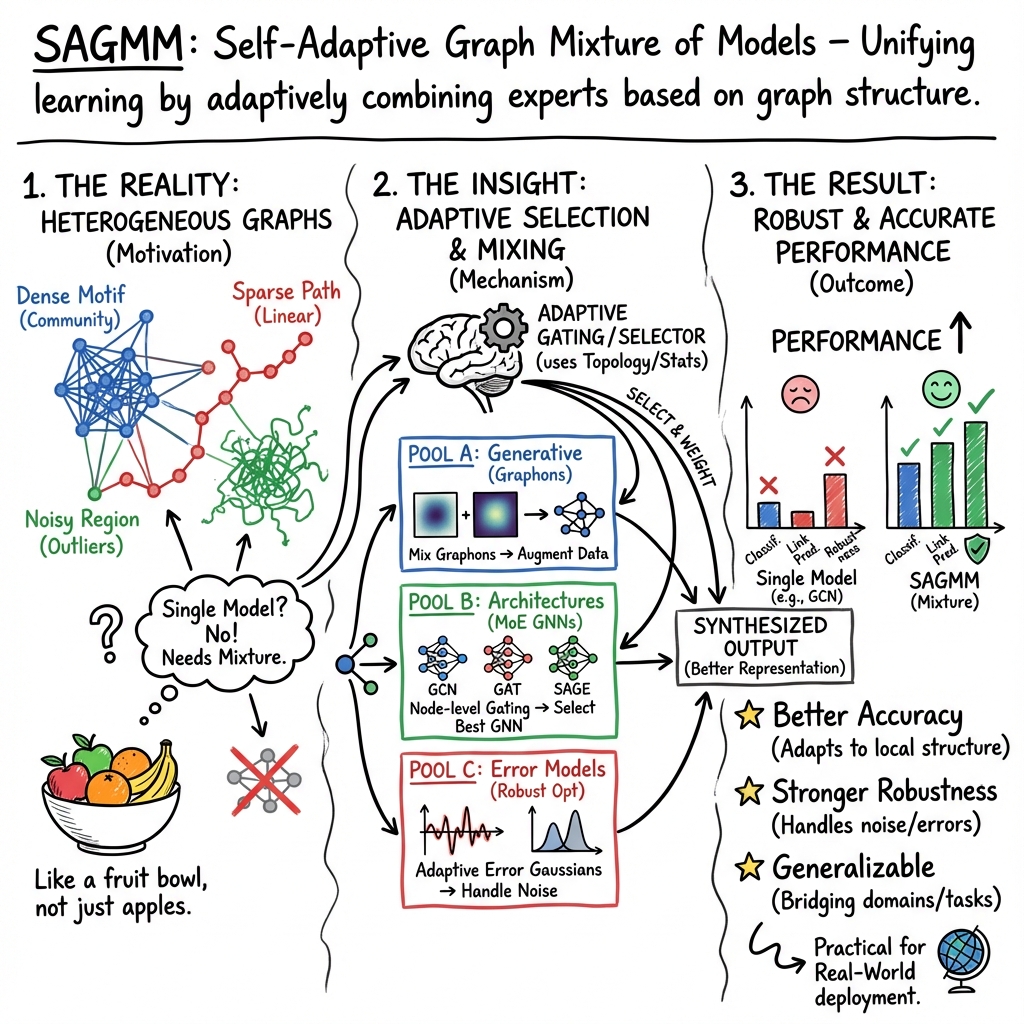
Self-Adaptive Graph Mixture Models (SAGMM)

• SAGMM is a framework that unifies graph learning, representation, and robust inference by adaptively combining multiple diverse models and experts based on graph structure.
• It employs explicit mixture modeling techniques such as graphon mixtures, motif-based clustering, and topology-aware gating to dynamically select and merge expert outputs.
• Empirical evaluations demonstrate SAGMM’s superior performance in tasks like node classification, link prediction, and robust graph optimization compared to traditional models.

Self-Adaptive Graph Mixture of Models (SAGMM) unifies graph learning, representation, and robust inference by adaptively combining multiple models or experts—either at the level of generative distributions, neural architectures, or error distributions—while leveraging graph structural properties to guide mixture assignments and model adaptation. SAGMM instances span from graphon mixture frameworks and domain-generalizing model mergers to robust graph optimization, all characterized by their capacity to discover, select, and efficiently synthesize diverse modeling components based on graph data statistics, topological cues, or latent mixture structure.

1. Core Principles and Formal Definitions

SAGMM builds on the observation that many real-world graph datasets are best interpreted as mixtures—over generative distributions, domains, or model architectures—rather than homogeneous samples from a single source. The formalism can target different modeling regimes:

• Graphon Mixtures: A graphon $W: [0,1]^2 \to [0,1]$ provides a nonparametric limit object encoding an edge probability kernel, from which finite graphs are sampled by latent variable draws and Bernoulli edge assignments. The mixture model assumption posits that each observed graph arises from a finite mixture $\{W_k\}_{k=1}^K$ with unknown $K$ (Azizpour et al., 4 Oct 2025).
• Mixture-of-Experts in GNNs: SAGMM maintains a heterogeneous expert pool $\{e_1, ..., e_{N_0}\}$, across diverse GNN architectures (e.g., GCN, GAT, SAGE, GIN, MixHop), and assigns mixture weights to each expert per node or graph based on input-adaptive gating informed by topological descriptors (Meena et al., 17 Nov 2025).
• Gaussian Mixture in Graph Optimization: For robust inference in factor graphs, model error terms as a mixture of $K$ zero-mean Gaussians, with parameters adaptively estimated through expectation–maximization jointly with state variables (Pfeifer et al., 2018).

These frameworks share three core mechanisms: (i) explicit mixture modeling; (ii) adaptive estimation or selection of components given graph structure, features, or errors; (iii) compositional inference where outputs from mixture components are selectively aggregated for downstream tasks.

2. Mixture Estimation and Adaptive Clustering

Graphon and Motif-Based Clustering:

Given observed graphs $D = \{G_t\}_{t=1}^T$, estimate underlying mixture components using motif (graph moment) densities:

• Compute motif densities $\hat t(F,G_t)$ for a fixed motif set $F_1, ..., F_m$ (e.g., all subgraphs with $k\leq4$ nodes), resulting in vectors $v_t \in \mathbb{R}^m$.
• Cluster $\{v_t\}$ (e.g., $K$-means, with $K\approx\lceil \log T \rceil$ or data-adaptive selection) to recover mixture assignments $\tau(G_t)$.
• For each cluster, apply a graphon estimation routine (e.g., SIGL) to obtain $W_k$ (Azizpour et al., 4 Oct 2025).

Domain Mixtures and Label-Conditional Generation:

In domain merging, assume the target domain lies in the convex hull of source distributions: $$\mathcal{G}_T = \sum_{i=1}^M \alpha_i \mathcal{G}_i$$. Since only pretrained models $f(\Theta_i)$ are available, a graph generator $\mathcal{P}_i$ optimizes node features and edge encoders to synthesize data $\mathcal{G}_i^*$ representative of each domain, using batch-norm and entropy regularization (Wang et al., 4 Jun 2025).

Error Mixtures via Expectation–Maximization:

In robust sensor fusion, embed an inner EM loop for Gaussian mixture estimation over graph factor residuals, nested within an outer gradient-based solver for state estimation, yielding a bi-level adaptive mechanism for multi-modal error structure (Pfeifer et al., 2018).

3. Model Selection, Attention Gating, and Expert Pruning

Topology-Aware Attention Gating (TAAG):

Assign mixture weights $g_{n,e}$ over experts for each node $n$ by extracting local/global topology features (e.g., $X^{(1)}=D^{-1}AX$, $X^{(2)}=(D^{-1}A)^2X$, and $p$ smallest Laplacian eigenvectors), followed by linear projection into Q/K/V and simple global attention (Meena et al., 17 Nov 2025). Sparse mask $M_{n,e}$ selects only experts with $Z'_{n,e} > T_e$. An auxiliary rule ensures every node receives at least one expert.

Gating in Domain Mixtures:

Sparse gating is implemented by scoring ($Q(G)$), Top-K selection, and softmax construction over experts, applied per (generated) sample. Each expert can be masked (with real-valued $\omega^j$ applied to a subset, commonly classifier head parameters) to enable domain shift adaptation while preserving knowledge (Wang et al., 4 Jun 2025).

Adaptive Pruning:

Periodically compute importance scores $I_t(e)$ for each expert; those below threshold $\eta$ are pruned to reduce computation. Auxiliary losses ($\mathcal{L}_{\rm imp}$ for expert load balancing, $\mathcal{L}_{\rm div}$ for gating diversity) promote robust specialization without mode collapse (Meena et al., 17 Nov 2025).

Training-Efficient Variant:

In SAGMM-PE, all expert GNNs are pretrained and frozen; only gating and task heads are updated during downstream adaptation.

4. Augmentation, Contrastive Learning, and Robust Inference

Graphon-Mixture-Aware Mixup (GMAM):

Generate graph augmentations by interpolating in the space of estimated graphons: $W_\lambda = \lambda W_a + (1-\lambda) W_b$, and sampling new graphs using fresh node latents and Bernoulli edge assignments. Labels are similarly mixed: $y^{\rm new} = \lambda y_a + (1-\lambda) y_b$. Extension to higher-order mixtures is immediate: $W = \sum_k \alpha_k \hat W_k$ (Azizpour et al., 4 Oct 2025).

Model-Aware Graph Contrastive Learning (MGCL):

Following clustering, augment edges using the estimated cluster-specific graphon, and in InfoNCE loss restrict negative pairs to samples from distinct clusters: $$\ell_t = -\log \frac{\exp(\mathrm{sim}(z_t,\tilde z_t)/\tau)} {\sum_{t':\tau(G_{t'})\neq \tau(G_t)}\exp({\mathrm{sim}(z_t,z_{t'})/\tau})}$$ This reduces "false negatives" and preserves true mixture component structure.

Robust Factor-Graph Optimization:

In dynamic sensor fusion, assign each residual a likelihood under a Gaussian mixture, updating both mixture parameters $\{w_k,\Sigma_k\}$ (via EM) and state variables $X$ (via nonlinear least-squares on summed mixture log-likelihood) at every time step. Robustness and self-tuning are achieved through this tight interleaving (Pfeifer et al., 2018).

5. Theoretical Guarantees

Graphon Cut Distance and Motif Density Bounds:

A novel theoretical guarantee establishes that, for all motifs $F$ of $k$ vertices and $e$ edges, with $G_1 \sim W_1$, $G_2 \sim W_2$, and $\delta_\square(W_1,W_2)\leq\epsilon$,

$$|\hat t(F,G_1) - \hat t(F,G_2)| \leq e(F)\epsilon + 2\sqrt{\frac{\ln(4/\eta)}{\lfloor N/k \rfloor} + \frac{e(F)}{N}\sqrt{2\ln\frac{4}{\eta}}}$$

holding with probability at least $1-2\eta$ (Azizpour et al., 4 Oct 2025). This links structural proximity in graphon space with observable motif statistics, enabling principled mixture component estimation.

Domain Generalization Upper Bound:

Given $M$ source domains and pretrained optimal models, the error of the mixture on $$\mathcal{G}_T = \sum_{i=1}^M \alpha_i \mathcal{G}_i$$ is upper-bounded by the sum of cross-validation errors between pairs of sub-learners, formalized using the $\mathcal{H}\Delta\mathcal{H}$-divergence (Wang et al., 4 Jun 2025).

EM Convergence in Robust Optimization:

Inner EM loops over residuals guarantee local optimum mixture parameters for fixed states. The outer blockwise alternation for state updates converges stably if state shifts are smooth and the sliding window scheme is narrow (Pfeifer et al., 2018).

6. Empirical Evaluation Across Regimes

Node and Graph Classification

• On ogbn-products (2.4M nodes): SAGMM achieves 82.91% versus GCN 75.54%, GAT 76.77%, prior mixtures ≤68.77% (Meena et al., 17 Nov 2025).
• On TUDatasets for graph classification: GMAM yields highest accuracy on 5/7 datasets, with up to +1.3% absolute improvement over strong augmentation baselines (Azizpour et al., 4 Oct 2025).

Link Prediction and Molecular Regression

• On ogbl-ddi: SAGMM achieves 74.20 HITS@20 vs. GraphSAGE 53.90, DA-MoE 45.58.
• On regression tasks (molfreesolv): SAGMM RMSE 2.15 (vs. 2.23 for GAT), indicating robust performance for molecular property prediction (Meena et al., 17 Nov 2025).

Robust Graph Optimization

• On UWB indoor localization and urban GNSS: Adaptive sum-mixture SAGMM yields up to 50% reduction in absolute trajectory error (ATE) relative to statically parameterized mixtures, and outperforms all tested robust estimators with only a modest (2×) computation overhead (Pfeifer et al., 2018).

Ablations and Sensitivity

• Ablations confirm the necessity of expert gating, masking, and diversity regularization for effective mixture selection. Removing mixture-adaptive components leads to sharp performance drops (e.g., $>20$ pp drop without gating) (Wang et al., 4 Jun 2025, Meena et al., 17 Nov 2025).
• Expert pruning reduces parameter count and inference time by 10–20% with negligible accuracy loss (Meena et al., 17 Nov 2025).

7. Extensions, Generalizations, and Practical Applications

Toward Fully Adaptive, Multi-Granular SAGMM:

• Motif-based clustering can be replaced or supplemented by spectral signatures, node embeddings, or dynamic, data-driven $K$ selection (e.g., silhouette analysis), enabling self-adaptive discovery of mixtures as data distributions shift (Azizpour et al., 4 Oct 2025).
• Mixtures can leverage higher-order motifs, weighted mixtures, and stochastic gating mechanisms to address rare or underrepresented graph populations.
• Domain merging can operate in source-free settings, reconstructing synthetic data through label-conditional graph generation when only model weights are available, and merging heterogeneous experts via sparse gating and adaptive masking for out-of-distribution generalization (Wang et al., 4 Jun 2025).
• In streaming or evolving data, on-the-fly reclustering, gating re-optimization, and model pruning yield scalable, deployment-ready SAGMM variants.
• In robust estimation tasks, the SAGMM paradigm enables automatic parameter tuning to match non-Gaussian, multi-modal error distributions, without manual intervention (Pfeifer et al., 2018).

A plausible implication is that SAGMM provides a common abstraction for multi-model, multi-domain, and multi-generator learning in graphs, bridging generative, discriminative, and robust estimation paradigms. This suggests strong relevance for heterogeneous knowledge integration, transfer learning, and robust real-world graph deployment.