Manifold-Constrained Hyper-Connections (mHC)

• mHC is a framework that applies manifold constraints to multi-stream residual connections, preserving identity mapping and ensuring stable gradient flows.
• It employs projections onto the Birkhoff polytope using the Sinkhorn-Knopp algorithm to enforce norm non-expansiveness and compositional closure in processing.
• Empirical results demonstrate that mHC improves training stability, accuracy, and memory efficiency compared to unconstrained hyper-connections.

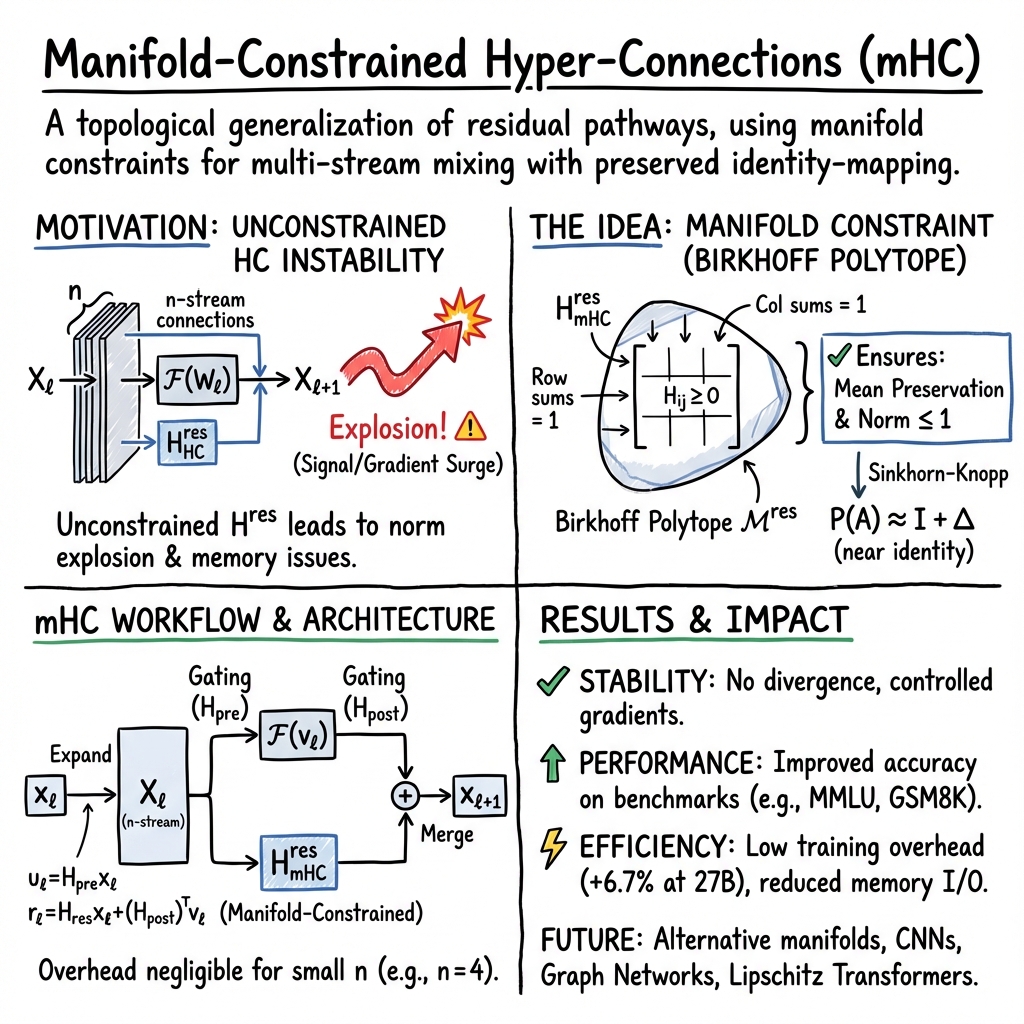
Manifold-Constrained Hyper-Connections (mHC) are a topological generalization of residual pathways in deep neural networks, designed to enable multi-stream mixing while rigorously preserving the identity-mapping property. As a principled extension of the Hyper-Connections (HC) architecture, mHC imposes a manifold constraint—specifically, projection onto the Birkhoff polytope (the set of doubly stochastic matrices)—on residual transformation matrices. This constraint provides compositional norm bounds and mean preservation, mitigating gradient pathologies and memory inefficiencies associated with unconstrained multi-stream residuals. mHC demonstrably improves training stability, downstream accuracy, and system efficiency at scale, and forms a flexible architectural primitive for next-generation foundational models (Xie et al., 31 Dec 2025).

1. Motivation and Historical Context

Residual connections, notably ResNet-style update rules of the form $x_{l+1} = x_l + \mathcal{F}(x_l, W_l)$, are foundational in deep learning due to their identity-mapping property, which guarantees feature-mean preservation and stabilizes deep gradient flows. Hyper-Connections (HC) [Zhu et al. 2024] generalize this paradigm by expanding the residual stream from dimension $C$ to $n\times C$ and introducing additional learnable mappings—$H^{pre}_l\in\mathbb{R}^{1\times n}$, $H^{post}_l\in\mathbb{R}^{1\times n}$, and $H^{res}_l\in\mathbb{R}^{n\times n}$. However, unconstrained HC transforms the residual pathway into $\prod_{i=1}^{L-l} H^{res}_{L-i}$ over $L-l$ layers, no longer guaranteeing norm or mean-preserving behavior, which can result in signal explosion/vanishing, severe gradient surges, and prohibitive memory I/O costs, particularly for large models (e.g., 27B parameters). This led to the search for a manifold-based constraint to restore the robust stability of classical residual architectures in a richer topological setting (Xie et al., 31 Dec 2025).

2. Manifold Projection and Identity Restoration

mHC addresses the instability in HC by constraining residual connection matrices to the Birkhoff polytope $$\mathcal{M}^{res} = \{ H\in\mathbb{R}^{n\times n} \mid H 1_n = 1_n, 1_n^T H = 1_n^T, H_{ij} \geq 0 \}$$—the convex hull of all $n\times n$ permutation matrices.

Key Manifold Properties

• Norm non-expansiveness: Any $H\in\mathcal{M}^{res}$ satisfies $\|H\|_2 \leq 1$, ensuring no signal amplification through the residual path.
• Compositional closure: $\mathcal{M}^{res}$ is closed under multiplication, so stacked layers preserve the manifold structure.
• Mean preservation: Exact restoration of the identity mapping property, with both row and column sums set to one.

Sinkhorn-Knopp Projection

Given an unconstrained $A\in\mathbb{R}^{n\times n}$, projection is accomplished by the Sinkhorn-Knopp algorithm:

• Set $A^{(0)} := \exp(A)$ for positivity.
• Alternate row- and column-normalization for a fixed $T_{max}\approx 20$ iterations: $A^{(t)} := T_r(T_c(A^{(t-1)}))$.
• $P(A) = A^{(T_{max})}$ approximates a doubly stochastic matrix.

Near the identity, $P(I+\Delta) \approx I+O(\Delta)$, so mHC realizes "identity plus small perturbation" and maintains contractive stability across layers.

3. mHC Architecture and Algorithmic Workflow

In a typical pre-norm Transformer block, the scalar residual gate is replaced by an $n$-stream residual structure with two gating maps and manifold-constrained mixing:

• Input Expansion: Duplicate $x_l \in \mathbb{R}^C$ to form $X_l \in \mathbb{R}^{n\times C}$, then flatten as $\tilde{x}_l \in \mathbb{R}^{nC}$.
• Gate and Residual Map Generation: Compute $a_{pre}, a_{post} \in\mathbb{R}^n$, $A_{res}\in\mathbb{R}^{n\times n}$ via linear projections and scaling.
• Manifold Projection and Application:
  • $H_{pre} = \sigma(a_{pre})$
  • $H_{post} = 2\sigma(a_{post})$
  • $H_{res} = \text{Sinkhorn}(e^{A_{res}})$
• Update Path: $u_l = H_{pre} x_l$; $v_l = \mathcal{F}(u_l; W_l)$; $r_l = H_{res} X_l + (H_{post})^T v_l$
• Stream Merge: $x_{l+1} = \text{Merge}(r_l)$, typically by averaging or projection.

The following table summarizes computational steps per layer:

Step	Operation	Output Dimension
Input Expansion	$X_l = \text{stack}_n(x_l)$	$n\times C$
Gate Projections	$a_{pre}, a_{post}, A_{res}$	$n$, $n$, $n\times n$
Sinkhorn Projection	$H_{res} = \text{Sinkhorn}(e^{A_{res}})$	$n\times n$
Residual Application	$r_l = H_{res} X_l + (H_{post})^T v_l$	$n\times C$
Merge	$x_{l+1} = \text{Merge}(r_l)$	$C$

For small $n$ (e.g., $n=4$), the computational overhead of the manifold projection is negligible relative to the main block $\mathcal{F}$.

4. Efficiency Engineering and System-Level Integration

mHC is implemented with several optimizations to control run-time overhead and peak memory usage:

• Kernel fusion: RMSNorm, linear projections, Sigmoid, and scaling are fused into custom kernels, reducing memory traffic.
• Mixed precision: Activations in bfloat16, weight multiplications in tfloat32, and accumulator/intermediate computations in FP32.
• In-place Sinkhorn: Sinkhorn iterations operate entirely in-register for $n\times n$ matrices, eliminating global memory access.
• Activation recomputation: Intermediate states ($X_l$, $H_{res}$, $H_{pre}$, $H_{post}$) are discarded after the forward pass and recomputed only as needed.
• DualPipe pipeline parallelism: Residual stream kernels are overlapped on a high-priority CUDA stream, with recompute blocks aligned to pipeline boundaries.

Notably, for $n=4$, end-to-end training time increases only by $+6.7\%$ for a 27B-parameter Transformer relative to baseline. Memory I/O per apply kernel is reduced from $(3n+1)C$ reads/$3nC$ writes to $(n+1)C$ reads/$nC$ writes.

5. Empirical Validation

Extensive experiments were performed on Mixture-of-Experts Transformers (DeepSeek-V3 backbone) at 3B, 9B, and 27B scale, with $n=4$ stream width. Key findings include:

• Stability: On 27B models, mHC maintains stable loss gap ($-0.021$ vs. baseline), while HC diverges at $\sim$12k steps. Gradient norms for mHC remain close to baseline, with HC exhibiting large spikes.
• Amax Gain Magnitude: mHC keeps single-layer $H^{res}$ gains $\approx 1 (\pm 0.02)$, with aggregate $\leq 1.6$, while unconstrained HC can reach $>3000$.
• Benchmarks: Across eight zero- and few-shot benchmarks, mHC consistently outperforms both baseline and HC:

Benchmark (shots)	Baseline	+HC	+mHC
BBH (3-shot)	43.8	48.9	51.0
DROP (3-shot)	47.0	51.6	53.9
GSM8K (8-shot)	46.7	53.2	53.8
HellaSwag (10-shot)	73.7	74.3	74.7
MATH (4-shot)	22.0	26.4	26.0
MMLU (5-shot)	59.0	63.0	63.4
PIQA (0-shot)	78.5	79.9	80.5
TriviaQA (5-shot)	54.3	56.3	57.6

Compute scaling curves (3B→9B→27B) show the loss advantage of mHC is preserved with increasing model size, and token scaling (for fixed 1T tokens) shows mHC ahead throughout training (Xie et al., 31 Dec 2025).

6. Theoretical Foundations and Future Extensions

Theoretical Guarantees

• Norm-nonexpansiveness: For $H \in \mathcal{M}^{res}$, $\|H\|_2 \leq 1$. This spectral bound prevents gradient explosion/vanishing.
• Compositional stability: The manifold’s closure under multiplication ensures whole-network stability for extended depth.
• Birkhoff polytope geometry: Each $H$ is a convex combination of $n\times n$ permutations, enabling controlled, unbiased mixing of residual streams.

Sketch of spectral bound: For any non-negative, doubly stochastic $H$, the maximum singular value $\leq 1$, following from Perron–Frobenius theory and the structure of stochastic matrices.

Extension Directions

• Alternative manifolds: Orthogonal (O($n$)), Stiefel, or symplectic manifolds could be used to enforce stricter or alternative invariances (e.g., energy preservation, exact spectral norm).
• mHC in CNNs: Applying n-stream residual mixing to widen ResNet planes is a plausible extension.
• Graph networks: Node-feature mixing with stochastic adjacency constraints may benefit from mHC-style design.
• Lipschitz Transformers: Combining mHC with scaled-dot-product attention to bound layerwise Lipschitz constants is anticipated as a future pursuit.

The mHC framework demonstrates that manifold-constraint of multi-stream residuals yields provable stability, scale transferability, and performance gains, and serves as a robust foundation for further theoretical and architectural expansions in topological model design (Xie et al., 31 Dec 2025).