mHC: Manifold-Constrained Hyper-Connections (2512.24880v1)
Abstract: Recently, studies exemplified by Hyper-Connections (HC) have extended the ubiquitous residual connection paradigm established over the past decade by expanding the residual stream width and diversifying connectivity patterns. While yielding substantial performance gains, this diversification fundamentally compromises the identity mapping property intrinsic to the residual connection, which causes severe training instability and restricted scalability, and additionally incurs notable memory access overhead. To address these challenges, we propose Manifold-Constrained Hyper-Connections (mHC), a general framework that projects the residual connection space of HC onto a specific manifold to restore the identity mapping property, while incorporating rigorous infrastructure optimization to ensure efficiency. Empirical experiments demonstrate that mHC is effective for training at scale, offering tangible performance improvements and superior scalability. We anticipate that mHC, as a flexible and practical extension of HC, will contribute to a deeper understanding of topological architecture design and suggest promising directions for the evolution of foundational models.
Sponsor
Paper Prompts
Sign up for free to create and run prompts on this paper using GPT-5.
Top Community Prompts
Explain it Like I'm 14
A simple guide to “Manifold‑Constrained Hyper‑Connections”
Overview: What is this paper about?
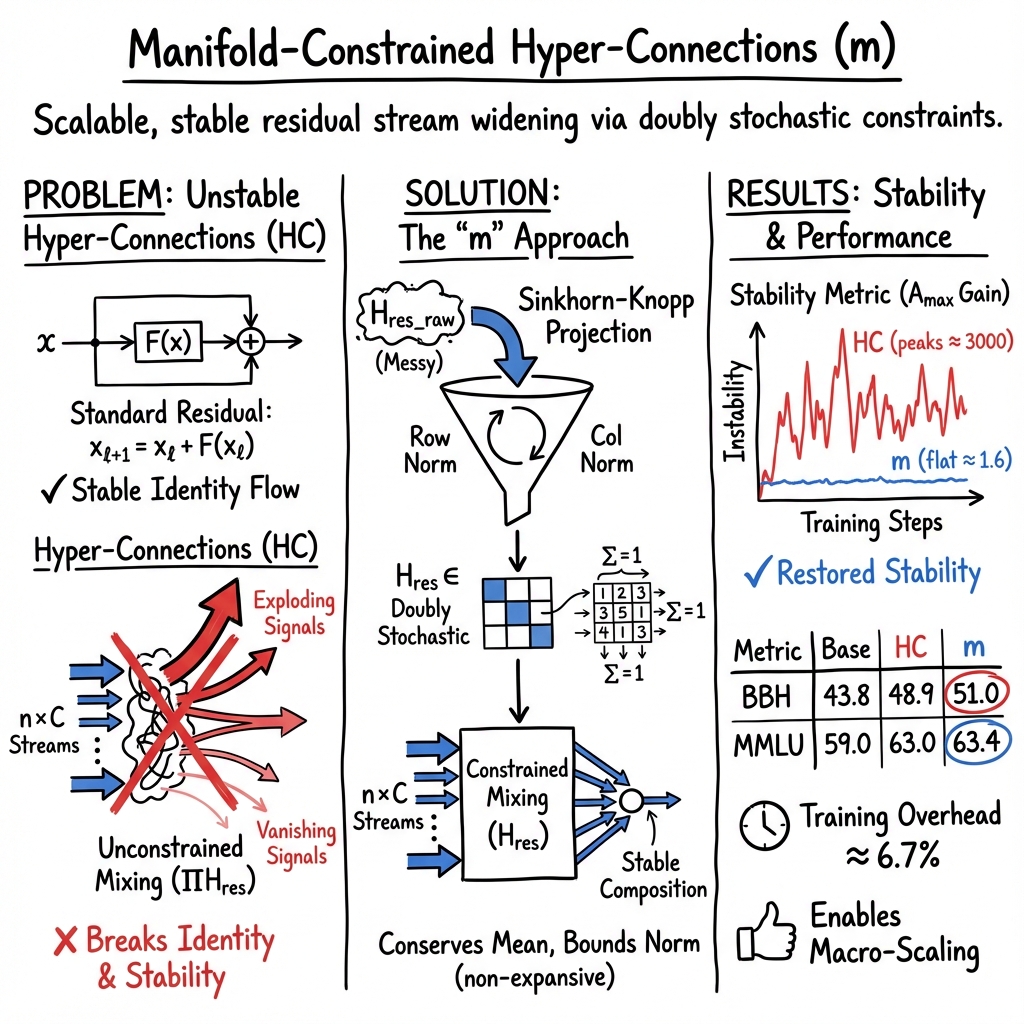
This paper is about making a kind of neural network connection—called a residual connection—work better when we make it more complex. Residual connections are like “fast lanes” that let information skip over layers so learning stays stable. A recent idea, Hyper‑Connections (HC), turns that single fast lane into several parallel lanes and lets them mix with each other, which can boost performance. But HC can become unstable when models get very big.
The authors propose a fix called Manifold‑Constrained Hyper‑Connections (MHC; abbreviated as “m” in the paper). It keeps the benefits of HC but restores stability by carefully controlling how those lanes mix—using a “fair mixing” rule—so training doesn’t blow up or fade away.
Key goals and questions
- Can we keep the performance gains of Hyper‑Connections without the training becoming unstable as models grow?
- Is there a simple rule that makes the mixing of multiple residual lanes “safe” across many layers?
- Can we do this efficiently so training speed and memory use stay practical for LLMs?
How the method works (in everyday terms)
First, some simple ideas:
- Residual connection: Imagine water flowing through a long pipe (the network). A residual connection is a straight bypass pipe that lets water flow through unchanged if needed. This makes the whole system easier to control and less likely to “burst” (explode) or “dry up” (vanish).
- Hyper‑Connections: Instead of one bypass pipe, HC creates several parallel pipes and adds valves to mix water between them. This can carry more information and help performance—but if the valves are set badly, pressure can grow too high or drop too low layer after layer.
- The problem: In HC, the mixing valves are free to choose any settings. Over many layers, tiny imbalances can compound, causing signals to explode or vanish. That’s instability.
What MHC changes:
- Fair‑mixing valves: MHC forces the mixing to follow a “fairness” rule. Think of it as a mixing bowl where each stream contributes some amount and the total in and out is conserved. In math, this rule says the mixing matrix is “doubly stochastic”: every row and every column adds up to 1, and all entries are non‑negative.
- Why this helps:
- It preserves the average signal (no net gain or loss).
- It keeps the overall size of signals from growing (non‑expansive), which prevents explosions.
- If you multiply many such fair‑mix matrices across layers, the result is still fair (closure under multiplication), so stability holds across the whole network.
- How they enforce fairness: They use the Sinkhorn‑Knopp algorithm, which is like repeatedly rescaling rows and columns so each sums to 1, until the matrix becomes a “fair‑mix” matrix. This set of fair‑mix matrices is known as the Birkhoff polytope—a fancy name for all possible fair shuffles and mixtures.
- Extra safeguards: They also keep the “read” and “write” mixing weights non‑negative so signals don’t cancel each other in weird ways.
Making it fast in practice:
- Kernel fusion: They combine steps that touch the same data into single GPU kernels (like doing all your errands in one trip), reducing memory traffic—the “memory wall” is a common bottleneck.
- Mixed precision and smart scheduling: They use lower‑precision where safe, and adjust the order of operations to save time.
- Recompute instead of store: To save memory, they throw away some temporary values during the forward pass and recompute them during the backward pass (cheaper than keeping everything in memory).
- Overlapped communication: In multi‑GPU training (pipeline parallelism), they overlap sending data with computing (like cooking while the laundry runs) so the GPUs stay busy.
Main findings and why they matter
- Training is much more stable: With standard HC, the “gain” of signals across layers could spike to extremely large values (around 3000 in their tests), a clear sign of instability. With MHC, those gains stay near 1, and even after many layers remain tightly bounded (around 1.6), making training smooth.
- Better performance: On a 27B‑parameter LLM, MHC consistently beats the baseline and usually beats HC on many tasks (like BBH, DROP, GSM8K, MMLU, PIQA, and TriviaQA). For example, compared to HC, MHC improved BBH by about 2.1% and DROP by about 2.3%.
- Scales well: Across model sizes (3B, 9B, 27B) and over longer training runs, the advantages persist. In other words, the fix still works as things get bigger.
- Low overhead: With 4 parallel residual lanes, MHC adds only about 6.7% extra training time—small compared to the stability and performance gains.
What this could mean going forward
- Safer, faster growth of big models: As LLMs keep getting larger, keeping training stable is crucial. MHC offers a practical way to widen and enrich the network’s information flow without risking instability.
- A blueprint for “safe connectivity”: The big idea—constraining network connections to a “safe shape” (a manifold like the Birkhoff polytope)—could inspire new designs. Different constraints might target different goals (stability, interpretability, robustness) while keeping training reliable.
- Better systems design for AI: The paper shows that good math ideas and good engineering must go together. Stability constraints plus careful GPU/kernel design can deliver both better accuracy and efficient training.
In short: MHC keeps the good parts of Hyper‑Connections (more information flow) while fixing the bad parts (instability) by enforcing fair, non‑expansive mixing. It trains big models more reliably, performs better on many tasks, and adds only a small training cost—making it a promising direction for building the next generation of large AI models.
Knowledge Gaps
Knowledge gaps, limitations, and open questions
The following list summarizes what remains missing, uncertain, or unexplored in the paper, aimed at guiding future research:
- Formal stability guarantees: Provide rigorous proofs that constraining
H_resto be doubly stochastic truly bounds forward/backward gains under composition across many layers, especially when Sinkhorn projections are approximate and gatesαare dynamic; quantify the Lipschitz constant of the full residual block and of the end-to-end network. - Sensitivity to Sinkhorn parameters: Systematically evaluate how the number of Sinkhorn iterations (
t_max), entropic regularization, and numeric precision affect constraint satisfaction (row/column sums ≈ 1), deviation magnitudes, training stability, and downstream performance; develop adaptive or learned iteration/temperature scheduling. - Gradients through Sinkhorn: Compare the custom backward recomputation to alternatives (implicit differentiation, unrolled differentiation, straight-through estimators); quantify gradient bias/variance and the impact on convergence; assess the stability of the backward kernel under mixed precision.
- Expressivity constraints of positive
H_preandH_post: Analyze whether enforcing non-negativity via Sigmoid limits representational capacity or hurts tasks where signed mixing is beneficial; ablate positive vs centered or signed parameterizations and measure the trade-offs. - Alternative manifold choices: Benchmark doubly stochastic against other constraints (orthogonal/unitary, spectral-normalized, normalized Laplacian, permutation mixtures, sparse doubly stochastic) to understand performance–stability trade-offs and derive principled selection criteria.
- Expansion rate scaling: Explore
nbeyond 4 (e.g., 2, 8, 16) to map stability, accuracy, throughput, memory, and communication overhead as functions ofn; identify compute-optimalnunder different hardware and pipeline budgets. - Architectural generality: Validate m beyond MoE Transformers—e.g., standard Transformers, vision Transformers/CNNs, diffusion models, RNNs—and assess whether the stability gains generalize across modalities and training regimes.
- Dataset and training transparency: Provide detailed corpus composition, token counts, and data domains; report variability across random seeds and statistical significance to substantiate stability and performance claims.
- Inference-time impact: Quantify latency, memory footprint, and throughput changes at inference; develop inference-specific kernel fusion or compaction strategies and evaluate compatibility with server deployment constraints.
- Quantization and low-precision compatibility: Test FP8/INT8 training/inference to determine whether DS projection and Sinkhorn remain stable; propose quantization-aware parameterizations if degradation occurs.
- Optimizer and normalization interactions: Study performance under different optimizers (AdamW, Adagrad, Lion) and normalization schemes (RMSNorm vs LayerNorm), including residual scaling variants; identify robust configurations.
- Clarify “identity mapping restoration”: Precisely define the conserved quantity (e.g., mean across streams) versus true identity mapping; introduce diagnostics beyond Amax Gain (e.g., energy conservation, per-channel statistics) and validate conservation empirically.
- Component ablations: Isolate contributions of the DS constraint vs infrastructure optimizations; test variants with DS on
H_resonly, with/without non-negativity onH_pre/H_post, and quantify each component’s effect on stability and accuracy. - Robustness at extreme depth: Evaluate very deep models and longer training horizons to detect potential over-smoothing or gradient underflow due to repeated DS mixing; design mechanisms (e.g., skip scaling, temperature control) to prevent over-regularization.
- Structure of learned mappings: Analyze
H_resmatrices for sparsity, entropy, proximity to permutations, and temporal evolution; study whether encouraging sparsity or structured mixing reduces I/O without harming performance. - Communication schedule portability: Validate DualPipe extensions across diverse interconnects (NVLink, PCIe, IB) and pipeline shapes; provide tuning guidelines for recomputation block size
L_runder pipeline boundaries and hardware constraints. - Task-specific regressions: Investigate benchmarks where m underperforms HC (e.g., MATH) to identify causes (e.g., loss of signed mixing) and test mitigations (e.g., partially signed constraints, task-aware manifold selection).
- Bounds and monitoring of composite gains: Derive worst-case and average-case bounds for forward/backward gains throughout training; develop runtime monitors and corrective strategies (e.g., penalties or projections) when deviations grow.
- Numerical stability of exponentiation: Examine overflow/underflow risks in
expused by Sinkhorn under mixed precision and largen; implement and evaluate clipping, log-domain computations, or stabilized parameterizations. - Interaction with MoE routing: Study whether DS mixing blurs or enhances expert specialization and load balancing; measure effects on MoE gate entropy, expert utilization, and cross-expert interference.
- Effects on parallelism strategies: Quantify how m impacts ZeRO/sequence parallelism, activation checkpointing, and sharding; provide integration recipes and memory–throughput trade-off analyses.
- Reproducibility and availability: Release code/kernels/configs and detailed runtime breakdowns to enable external validation of the reported 6.7% overhead (for
n=4) and performance gains across scales and hardware.
Glossary
- Amax Gain Magnitude: A metric capturing worst-case amplification by a mapping via maximum absolute row/column sums, used to assess propagation stability. "We refer to these metrics as the Amax Gain Magnitude of the composite mapping."
- Birkhoff polytope: The convex set of all doubly stochastic matrices; equivalently, the convex hull of permutation matrices. "m utilizes the Sinkhorn-Knopp algorithm~\citep{sinkhorn1967concerning} to entropically project $\mathcal{H}_{l}^{\mathrm{res}$ onto the Birkhoff polytope."
- Compositional closure: A property where a set is closed under a given operation; here, doubly stochastic matrices remain doubly stochastic under multiplication. "Compositional Closure: The set of doubly stochastic matrices is closed under matrix multiplication."
- Compute scaling curve: A plot showing performance versus compute budgets across model/data scales. "(a) Compute Scaling Curve."
- Convex combination: A weighted sum of vectors with nonnegative weights summing to one. "the operation $\mathcal{H}_{l}^{\mathrm{res}\mathbf{x}_l$ functions as a convex combination of the input features."
- DualPipe schedule: A pipeline-parallel training schedule that overlaps communication and computation across stages. "Specifically, we adopt the DualPipe schedule~\citep{liu2024deepseek_v3}, which effectively overlaps scale-out interconnected communication traffic, such as those in expert and pipeline parallelism."
- Doubly stochastic matrix: A nonnegative square matrix with each row and column summing to one. "We restrict {l} to be a doubly stochastic matrix, which has non-negative entries where both the rows and columns sum to 1."
- Entropic projection: Projection using entropy-regularized normalization (e.g., Sinkhorn) onto a constraint set. "m utilizes the Sinkhorn-Knopp algorithm~\citep{sinkhorn1967concerning} to entropically project $\mathcal{H}_{l}^{\mathrm{res}$ onto the Birkhoff polytope."
- FLOPs: Floating point operations; a measure of computational cost. "HC significantly increases topological complexity without altering the computational overhead of individual units regarding FLOPs."
- Gradient checkpointing: A memory-saving technique that recomputes activations during backpropagation. "often necessitating gradient checkpointing to maintain feasible memory usage."
- Grouped-Query Attention (GQA): An attention variant that groups queries to reduce compute/memory. "such as Multi-Query Attention (MQA)~\citep{shazeer2019fast}, Grouped-Query Attention (GQA)~\citep{ainslie2023gqa}, and Multi-Head Latent Attention (MLA)~\citep{liu2024deepseek}."
- Hyper-Connections (HC): An architecture that widens and mixes residual streams via learnable mappings. "Recently, studies exemplified by Hyper-Connections (HC)~\citep{zhu2024hyper} have introduced a new dimension to the residual connection and empirically demonstrated its performance potential."
- Identity mapping property: The property that a signal passes unchanged through layers, stabilizing training. "this diversification fundamentally compromises the identity mapping property intrinsic to the residual connection"
- Kernel fusion: Combining multiple operations into one GPU kernel to reduce memory bandwidth overhead and improve throughput. "To ensure efficiency, we employ kernel fusion and develop mixed precision kernels utilizing TileLang~\citep{wang2025tilelang}."
- Manifold: A mathematical space used to constrain parameters; here, the set of doubly stochastic matrices. "projects the residual connection space of HC onto a specific manifold"
- Memory wall: The performance bottleneck caused by memory bandwidth/latency dominating runtime. "which is widely referred to as the ``memory wall''~\citep{dao2022flashattention}."
- Mixed-precision kernels: GPU kernels that use multiple numerical precisions to balance speed and accuracy. "develop mixed precision kernels utilizing TileLang~\citep{wang2025tilelang}."
- Mixture-of-Experts (MoE): A sparse neural architecture routing inputs to a subset of expert networks. "FFNs have been generalized into sparse computing paradigms via Mixture-of-Experts (MoE)~\citep{shazeer2017outrageously, lepikhin2020gshard, fedus2022switch}"
- Multi-Head Latent Attention (MLA): An attention variant that reduces memory footprint by using latent representations. "Multi-Head Latent Attention (MLA)~\citep{liu2024deepseek}"
- Multi-Query Attention (MQA): An attention variant that shares keys/values across multiple queries to reduce cost. "Multi-Query Attention (MQA)~\citep{shazeer2019fast}"
- Outer-product memory matrix: A matrix formed by outer products to store features across layers. "the Residual Matrix Transformer (RMT)~\citep{mak2025residual} replaced the standard residual stream with an outer-product memory matrix to facilitate feature storage."
- Permutation matrix: A square binary matrix with exactly one 1 per row and column, representing a permutation. "which is the convex hull of the set of permutation matrices."
- Pipeline parallelism: A distributed training technique that partitions model layers across devices and overlaps microbatches. "In large-scale training, pipeline parallelism is the standard practice for mitigating parameter and gradient memory footprints."
- Pre-norm Transformer: A Transformer variant applying layer normalization before attention/FFN sublayers. "Focusing on the widely adopted pre-norm Transformer~\citep{vaswani2017attention} architecture, we analyze the I/O patterns inherent to HC."
- Pre-training scaling laws: Empirical laws relating optimal model/data/compute scaling for training. "Consequently, HC offers a new avenue for scaling by adjusting the residual stream width, complementing the traditional scaling dimensions of model FLOPs and training data size discussed in pre-training scaling laws~\citep{Hoffmann2022Chinchilla}."
- Residual Matrix Transformer (RMT): An architecture that replaces residual streams with outer-product memory matrices. "the Residual Matrix Transformer (RMT)~\citep{mak2025residual} replaced the standard residual stream with an outer-product memory matrix"
- Residual stream: The pathway carrying features across layers; here widened to multiple parallel streams. "By expanding the width of the residual stream and enhancing connection complexity"
- RMSNorm: Root Mean Square Layer Normalization, normalizing by RMS rather than mean/variance. "RMSNorm(\cdot)~\citep{zhang2019root} is applied to the last dimension"
- Sinkhorn-Knopp algorithm: An iterative normalization method to obtain a doubly stochastic matrix. "m utilizes the Sinkhorn-Knopp algorithm~\citep{sinkhorn1967concerning}"
- Spectral norm: The largest singular value of a matrix, bounding amplification in linear mappings. "The spectral norm of a doubly stochastic matrix is bounded by 1"
- TileLang: A framework for implementing high-performance GPU kernels with tiling and fusion. "utilizing TileLang~\citep{wang2025tilelang}"
- Token scaling curve: A plot of model performance over the number of training tokens within a run. "(b) Token Scaling Curve."
- Topological complexity: The richness of connectivity patterns (paths/links) in a network architecture. "HC significantly increases topological complexity without altering the computational overhead of individual units regarding FLOPs."
Practical Applications
Immediate Applications
The following applications can be deployed now with modest engineering effort, leveraging the paper’s architecture (manifold-constrained residual mixing), stability diagnostics, and systems optimizations.
- Stable multi-stream residuals for LLM pretraining and finetuning (software/AI infrastructure, cloud)
- Use manifold-constrained hyper-connections (doubly stochastic residual mixing with Sinkhorn-Knopp) to improve training stability and scalability over standard Hyper-Connections while preserving performance gains.
- Products/workflows: PyTorch/DeepSpeed/Megatron modules implementing the m layer; training recipes with default hyperparameters (e.g., small gating init, ~20 Sinkhorn iterations, mixed-precision kernels).
- Dependencies/assumptions: Availability of fused kernels or efficient autograd for Sinkhorn; GPU support for mixed precision; tested expansion rates n≈4.
- Reduced training failures and compute waste in long runs (industry-wide, cloud providers)
- Replace unconstrained residual mixing with the doubly stochastic variant to avoid loss spikes/NaNs and restarts in multi-week training.
- Tools: Stability monitors emitting per-layer Amax Gain Magnitude (max row/column sums) and alerts; automatic gradient clipping thresholds informed by those metrics.
- Dependencies: Logging hooks at each block; negligible runtime overhead for metric computation.
- More robust domain finetuning for regulated sectors (healthcare, finance, legal)
- Apply m during finetuning (supervised or preference optimization) to reduce hyperparameter sensitivity and catastrophic divergence in domain adaptation.
- Tools/products: Domain-tuned LLM checkpoints using m; finetuning templates for EHR summarization, KYC/AML document analysis, compliance Q&A.
- Dependencies: Integration with existing finetuning stacks; validation on domain datasets; audit of numerical stability with mixed precision.
- Throughput-preserving multi-stream residuals via systems optimizations (software/ML systems)
- Adopt the paper’s kernel fusion, mixed-precision pathways, recomputation block sizing, and DualPipe schedule tweaks to keep the overhead of n-stream residuals modest (~6–7% at n=4).
- Products/workflows: Plugin for distributed training frameworks (e.g., DeepSpeed/Megatron) that injects fused m kernels, recompute policy (optimal Lr≈sqrt(nL/(n+2))), and high-priority stream scheduling.
- Dependencies: Ability to control CUDA streams and kernel persistence; pipeline boundaries aligned with recompute blocks.
- Diagnostic suite for residual-topology instability (academia, software tooling)
- Use Amax Gain Magnitude (forward/backward max row/column sums) to diagnose exploding/vanishing composite residual mappings in deep models, even without adopting m.
- Tools: Lightweight library that computes per-layer gain metrics and surfaces heatmaps similar to the paper; CI gates for new architectures.
- Dependencies: Access to activations or coefficients per block; tolerance for small profiling overhead.
- Drop-in replacement for existing HC experiments (research labs, model developers)
- Swap HC’s unconstrained residual matrix with the doubly stochastic projection (20-step Sinkhorn) to recover the identity-mapping property and maintain expressivity.
- Products/workflows: “HC→m” migration guide, including initialization, iteration counts, and performance baselines on 3B/9B/27B-scale models.
- Dependencies: Minimal; code-level change and retuning learning-rate warmup may be required.
- Incremental quality gains for user-facing applications (education, productivity, search)
- Deploy m-pretrained or m-finetuned LLMs for tutoring, coding assistants, and retrieval-augmented QA to realize modest but consistent accuracy improvements (e.g., MMLU, BBH, DROP).
- Products: SaaS endpoints/SDKs offering “stable-topology” models; A/B tests in production to quantify improvements.
- Dependencies: Availability of m-based checkpoints; negligible inference overhead versus baseline.
- Energy and cost efficiency via fewer restarts and better IO scheduling (energy, sustainability reporting)
- Lower embodied compute and carbon by preventing instability-related reruns and by reducing memory traffic through fused kernels and recompute policy.
- Workflows: Training pipeline dashboards that track avoided restarts and estimated energy saved.
- Dependencies: Ops visibility; alignment with sustainability metrics frameworks.
Long-Term Applications
These directions are promising but require further research, scaling validation, or ecosystem support.
- Topology-aware routers and interpretable connectivity (software, research)
- Extend from doubly stochastic to other manifolds (e.g., sparse doubly stochastic, orthogonal/Stiefel) for learnable, stable, and interpretable residual routing; leverage Birkhoff polytope geometry to approximate convex combinations of permutations.
- Products: Residual Topology Compiler that selects/learns manifold constraints per layer and generates fused kernels.
- Dependencies: Theory and empirical validation across tasks; efficient sparse Sinkhorn variants; autotuning.
- Cross-modality and reinforcement learning stabilization (vision, speech, robotics)
- Apply m to deep cross-layer fusion in VLMs/ASR and to policy/value networks in long-horizon RL to improve credit assignment and prevent gradient pathologies.
- Products: Stable multi-stream backbones for VLMs; robot policy stacks with better long-horizon learning.
- Dependencies: Transferability beyond language; domain-specific kernel adaptations; robustness under off-policy/RL noise.
- Continual and federated learning with non-expansive mixing (enterprise, mobile/edge)
- Use non-expansive, conserved residual mappings to mitigate forgetting and stabilize updates across rounds/sites; enable deeper on-device models with constrained memory.
- Products: Federated LLM training frameworks with m; on-device assistants with deeper yet stable backbones.
- Dependencies: Privacy/communication constraints; sparse/quantized m kernels; device-specific accelerators.
- Hardware–algorithm co-design (semiconductor, cloud)
- Incorporate Sinkhorn-like normalization and multi-stream residual primitives into accelerators (matrix engines with row/column normalization and low-precision-safe exp/log).
- Products: ISA extensions and libraries for manifold projections; scheduler support for high-priority preemption.
- Dependencies: Vendor adoption; cost–benefit studies; compiler support (TileLang/TVM/XLA).
- Standards for training stability reporting (policy, governance)
- Create benchmarks and reporting guidelines that include conservation/stability metrics (e.g., Amax Gain distributions) for foundation models, alongside loss and accuracy.
- Products: Compliance checklists, “stability cards,” and audit tools for large training runs.
- Dependencies: Community consensus; reproducibility frameworks; minimal overhead metric computation.
- Automated manifold selection and adaptive constraint strength (AutoML)
- Learn per-layer manifold types and projection strengths based on training signals (e.g., increase sparsity or temperature when gains drift).
- Products: Controllers that monitor gains/grad norms and adapt Sinkhorn iterations or constraints online.
- Dependencies: Reliable online estimators; stability guarantees under adaptive projections.
- Extreme-depth and trillion-parameter scaling (foundation models)
- Exploit compositional closure and non-expansiveness to safely push depth/width while retaining signal conservation, enabling more predictable convergence in ultra-large models.
- Products: Next-generation foundation models with deeper residual topologies and reduced instability risk.
- Dependencies: Demonstrations beyond 27B; optimizer and LR schedule co-design; cluster-scale systems validation.
- Sparse communication and IO redesign for multi-stream residuals (distributed systems)
- Combine sparse manifold constraints with compressed activation transfer to shrink pipeline bubbles and inter-stage bandwidth.
- Products: Communication stacks that understand structured residual mixing; topology-aware staging.
- Dependencies: Robust sparse Sinkhorn; error-compensated compression; scheduling algorithms.
- Pedagogical toolkits for topology-centric architecture education (academia, education tech)
- Use m and its diagnostics to teach how macro-architecture topology affects optimization and representation learning.
- Products: Course labs, interactive visualizations (heatmaps of residual mixing and gain metrics).
- Dependencies: Open datasets/checkpoints; approachable libraries for students.
Collections
Sign up for free to add this paper to one or more collections.