Grassmann Flows: Dynamics on Manifolds

Updated 24 December 2025

Grassmann flows are continuous-time dynamical systems on Grassmann manifolds that generalize geodesic, gradient, and Riccati flows.
They underpin techniques in eigenvalue computation, integrable systems like the KP hierarchy, and numerical algorithms using explicit exponential maps.
The theory extends to infinite-dimensional settings with operator-valued ODEs and PDEs, unifying applications in topology, optimization, and machine learning.

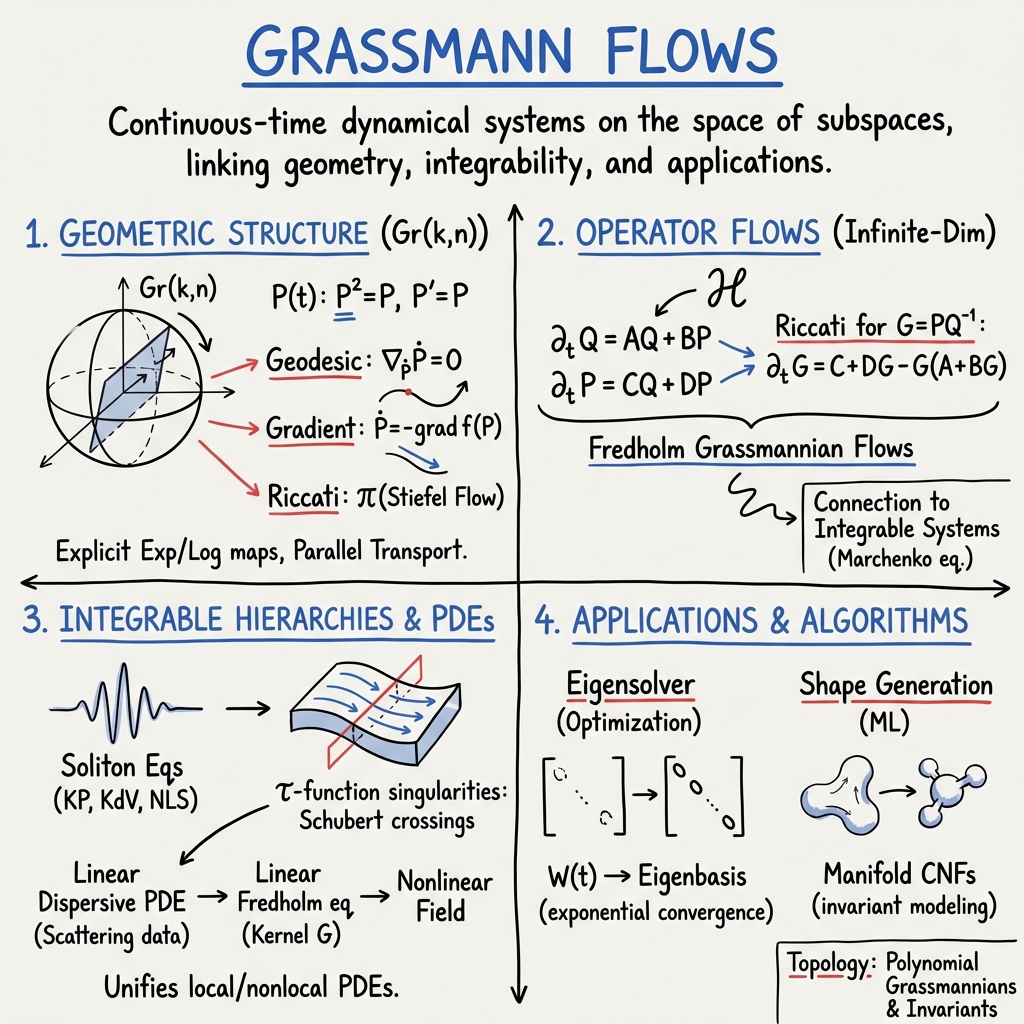
Grassmann flows refer to continuous-time dynamical systems evolving on Grassmann manifolds, the spaces of $k$ -dimensional linear subspaces of $\mathbb R^n$ (or more generally a Hilbert space). These flows generalize geodesic and gradient flows, Riccati-type evolution equations, and integrable hierarchies; they play a central role in diverse domains including integrable systems, eigenvalue computation, geometric optimization, and manifold-based machine learning. The theory encompasses finite-dimensional and infinite-dimensional cases, the geometry of tangent and cotangent bundles, and various realization procedures via operator-valued ODEs and PDEs.

1. Geometric Structure of Grassmann Flows

A Grassmann flow is formally an ODE or PDE defined on the Grassmann manifold $\mathrm{Gr}(k,n)$ or its infinite-dimensional generalization $\mathrm{Gr}(\mathcal H, \mathcal V)$ , describing the evolution of a subspace in time. In the finite-dimensional case, the Grassmannian admits two principal representations: quotient space $O(n)/(O(k)\times O(n-k))$ and the set of symmetric rank- $k$ projectors, with tangent space $T_P\mathrm{Gr}(n,k) = \{\Delta \in \mathrm{Sym}_n: P\Delta+\Delta P = \Delta\}$ (Bendokat et al., 2020). The canonical Riemannian metric is $g_P(\Delta_1,\Delta_2)=\tfrac{1}{2}\mathrm{tr}(\Delta_1\Delta_2)$ .

Flows considered on the Grassmannian include:

Geodesic flows: Integral curves $P(t)=\mathrm{Exp}_{P_0}(t\Delta)$ following the geodesic equation $\nabla_{\dot{P}}\dot{P}=0$ .
Riemannian gradient flows: $\dot{P} = -\mathrm{grad} f(P)$ , projecting the Euclidean gradient onto the tangent space.
Riccati flows and Fredholm flows: Evolution equations arising from projecting linear flows on (Stiefel) frames down to the Grassmannian.

Grassmann flows are integrable and efficiently computable via explicit formulas for exponential and logarithm maps, parallel transport, and Ricci curvature. Higher-order Runge–Kutta schemes are derivable from these geometric constructions (Bendokat et al., 2020).

2. Infinite-Dimensional Grassmannian and Operator Flows

For Hilbert spaces, the Fredholm Grassmannian consists of closed subspaces $W\subset \mathcal H$ such that the projection onto a fixed subspace $\mathcal V$ is Fredholm and onto $\mathcal V^\perp$ is Hilbert–Schmidt. In a local chart, subspaces are represented as graphs $W=\{v+Gv: v\in \mathcal V\}$ with Hilbert–Schmidt $G$ (Doikou et al., 2020, Doikou et al., 2019).

Flows on the infinite-dimensional Grassmannian are governed by systems of operator-valued ODEs: $\begin{aligned} \partial_t Q &= AQ + BP, \ \partial_t P &= CQ + DP, \end{aligned}$ with the nonlinear Riccati evolution for $G = PQ^{-1}$ ,

$\partial_t G = C + D G - G(A + B G).$

The connection to integrable systems is made through the reduction to the Gel’fand–Levitan–Marchenko equations via kernel representations and the Pöppe product rule (Beck et al., 2017, Doikou et al., 2020).

3. Integrable Hierarchies and KP Flow Realization

Grassmann flows are foundational to the study of integrable hierarchies, with soliton equations such as KP, KdV, and NLS reinterpreted as flows on appropriate Grassmannians. The $\tau$ -function construction for the real Grassmannian $\mathrm{Gr}(k,n)$ involves Wronskians of exponential solutions parameterized by multitime variables, yielding flows governed by the KP hierarchy (Casian et al., 2010).

Singularities (zeros of the $\tau$ -function) correspond to crossings of Schubert boundaries in the Grassmannian and allow explicit combinatorial construction of incidence graphs encoding the integral cohomology of $\mathrm{Gr}(k,n)$ . These graphs distinguish orientable and non-orientable cases via sign patterns and relate Betti numbers to Poincaré polynomials and $\mathbb F_q$ -point counts via Gaussian binomials. The number of singularities along the KP flow provides both topological invariants and arithmetic enumerations (Casian et al., 2010).

For higher $N$ -dimensional integrable systems, closedness of naturally defined differential $(N-1)$ -forms $\Omega_{N-1}$ on $\mathrm{Gr}(N-1,N+1)$ induces hierarchies such as Liouville (N=2), dispersionless KP (N=3), Dunajski, and self-dual Maxwell equations, unified under the “Grassmann flow” umbrella (Bogdanov et al., 2012).

4. Fredholm Grassmannian Flows in Nonlinear PDEs

Fredholm Grassmannian flows serve as a powerful linearization principle for nonlinear PDEs with both local and nonlocal nonlinearities. Solutions to systems such as matrix NLS, mKdV, and potential KdV, including their non-commutative and nonlocal variants, are constructed by:

Solving the linear dispersive PDE for the scattering data operator (Hankel form).
Solving a linear Fredholm (Marchenko-type) equation for the kernel $G$ that parametrizes the solution subspace.
Extracting the nonlinear field as a functional of $G$ (often its diagonal value) (Beck et al., 2017, Doikou et al., 2019, Doikou et al., 2020).

This approach subsumes local and nonlocal, commutative and non-commutative, and reverse-time/space integrable systems, offering unification of direct and inverse scattering methods.

5. Grassmann Flows in Optimization and Machine Learning

Gradient flows and continuous normalizing flows (CNFs) defined on the Grassmann manifold have direct application in numerical linear algebra and generative modeling:

Quasi-Grassmannian gradient flows (Editor’s term): These flows solve eigenvalue problems for symmetric coercive operators by evolving a subspace $W(t)$ under projected gradients, guaranteeing exponential convergence to an orthonormal eigenbasis without explicit re-orthogonalization, thus affording high numerical stability (Wang et al., 25 Jun 2025).
Manifold CNFs in shape generation: CNFs on $\mathrm{Gr}(k,n)$ parameterize probability densities on subspace-type shape spaces, leveraging the quotient structure to factor out rotational and inversion symmetries. Training involves ODEs on horizontal lifts, retractions into the Stiefel manifold, and Riemannian divergence computations, yielding robust, invariant generative models for molecular and geometric data (Yataka et al., 2022).

Algorithmic implementations utilize explicit matrix formulas for exponential/logarithm maps, horizontal projections, and cost-efficient ODE integration schemes (Bendokat et al., 2020, Yataka et al., 2022).

6. Grassmann Flows in Topology and Homotopy Theory

Grassmannian flows also play a role in topological classification of traversing flows on manifolds with boundary. Spaces of real polynomials with constrained divisors $\mathcal P_d^{\mathbf c\Theta}$ serve as “polynomial Grassmannians,” classifying equivalence (quasitopy) classes of convex pseudo-envelops and encapsulating combinatorial boundary-contact patterns. The cohomology and stabilization properties of these spaces encode characteristic classes and invariants for families of flows, with direct correspondence established via homotopy-theoretic bijections (Katz, 2022).

Pullbacks to cohomology yield generalized Arnold–Vassiliev invariants and stabilization as $d\to\infty$ , cementing the role of polynomial Grassmannians as classifying spaces in flow topology.

7. Computational Methods and Numerical Implications

Matrix-based algorithms for Grassmann flows—including explicit and implicit integration schemes—leverage SVD routines, projection/retraction methods, and parallel transport along geodesics (Bendokat et al., 2020). The availability of closed-form analytical solutions for projected gradient flows supports numerically robust eigensolver design (Wang et al., 25 Jun 2025). In high-dimensional or infinite-dimensional cases, solution strategies invoke Fredholm determinant theory and integral equation solvers, sidestepping the instability of time-stepping nonlocal nonlinear PDEs (Beck et al., 2017, Doikou et al., 2019).

Empirical results confirm exponential stability and accuracy for eigenvalue problems, invariant modeling in shape generation, and efficient reconstruction of solutions to integrable PDEs.

Grassmann flows synthesize advances in modern geometry, operator theory, integrable systems, algebraic topology, and computational mathematics; they serve as both a unifying theoretical structure and a practical foundation for algorithms in high-dimensional, symmetry-rich, and nonlinear scientific domains (Casian et al., 2010, Bogdanov et al., 2012, Beck et al., 2017, Doikou et al., 2020, Bendokat et al., 2020, Katz, 2022, Yataka et al., 2022, Wang et al., 25 Jun 2025, Doikou et al., 2019).