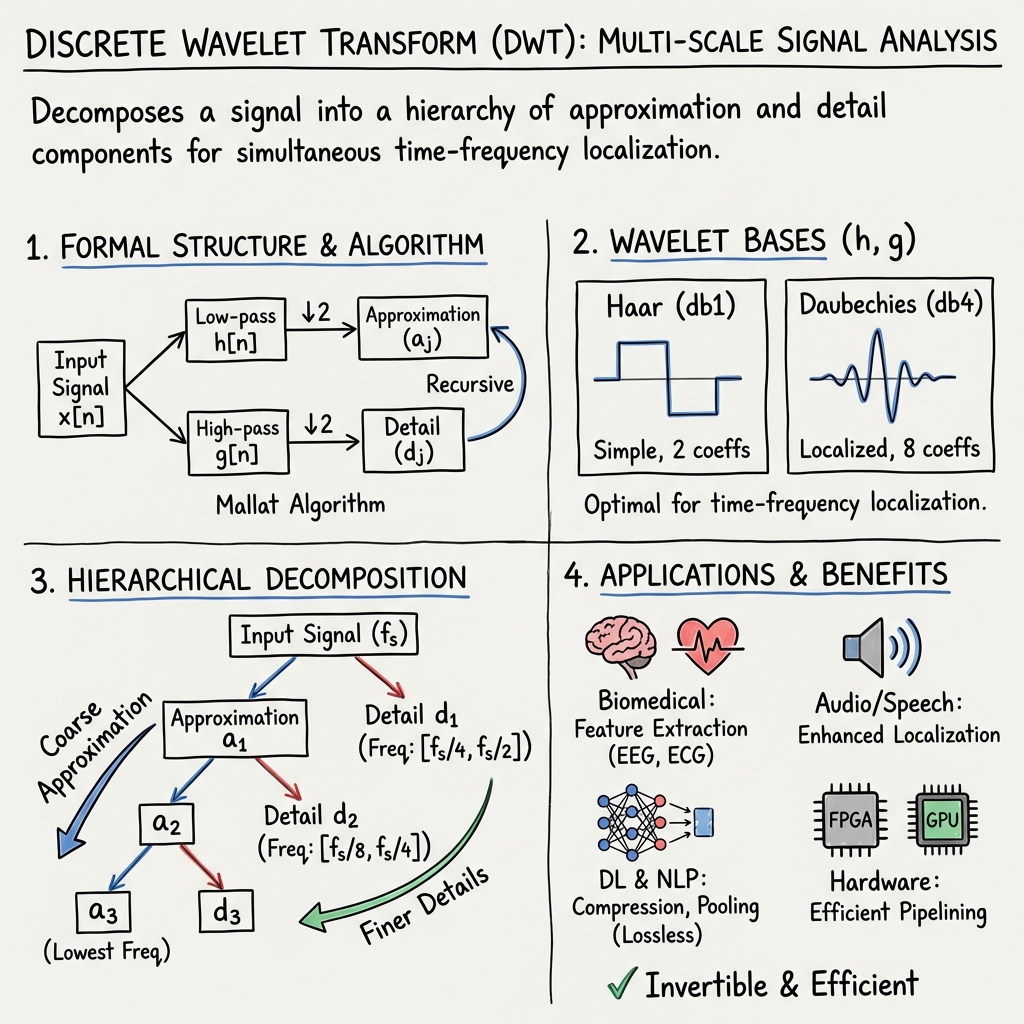
Discrete Wavelet Transform (DWT) Overview
- DWT is a multi-scale signal analysis method that decomposes discrete signals into approximation and detail components, capturing both frequency and temporal localization.
- It employs filter banks such as Daubechies and Haar to enable perfect reconstruction via the Mallat algorithm, ensuring efficient time-frequency representation.
- DWT finds diverse applications in biomedical signal processing, audio analysis, NLP embedding compression, and deep learning, offering efficient and invertible feature extraction.
The discrete wavelet transform (DWT) is a multi-scale signal analysis framework that decomposes a discrete input signal into a hierarchy of approximation and detail components, capturing both frequency and temporal localization. DWT underpins a wide range of applications, from feature extraction in biomedical and audio signals to dimensionality reduction in NLP, compression, and as a computational primitive in modern neural architectures and hardware accelerators.
1. Theoretical Foundations and Formal Structure
DWT is grounded in multiresolution analysis (MRA), which constructs a nested sequence of subspaces capturing increasingly coarse approximations of a signal. The scaling function spans at shift and scale:
where is the mother wavelet. Discrete signals yield approximation () and detail () coefficients as inner products with these bases:
The DWT can be efficiently realized by a perfect-reconstruction two-band filter bank (Mallat algorithm) using low-pass () and high-pass () FIR analysis filters. For 1D signals, the transform proceeds recursively:
with reconstruction given by
In orthogonal wavelets (e.g., Daubechies), , ; for biorthogonal families, distinct dual filters are used and must satisfy joint perfect reconstruction conditions (Tarafdar et al., 5 Apr 2025).
DWT decomposes 1D signals into approximation and detail bands at each level; for 2D (images) and higher dimensions, separable, axis-wise applications produce up to subbands per stage (Tarafdar et al., 5 Apr 2025, Ma et al., 2018).
2. Wavelet Filter Design and Choice of Basis
The spectral and localization properties of DWT hinge on the design of the mother wavelet and its associated (h, g) filter coefficients. Principal families include:
| Wavelet | Vanishing Moments | Filter Length | hn example |
|---|---|---|---|
| Haar | 1 | 2 | |
| db2 | 2 | 4 | |
| db4 | 4 | 8 |
Daubechies (dbN) wavelets, with vanishing moments, are optimal for time-frequency localization, making them the standard for biomedical signal segmentation (Feudjio et al., 2021, Noyum et al., 2021). Orthogonality is typically preferred for energy conservation and invertibility, though biorthogonal wavelets (e.g., CDF 9/7 used in JPEG 2000) are employed for symmetric or linear-phase requirements (0710.4812).
The paper (Guharoy et al., 2021) does not report the basis selection, while in (Feudjio et al., 2021), db2 and db4 are directly compared and tabulated for their coefficients; db4 is selected for morphological compatibility with QRS complexes, and db2/db4 for EEG rhythms at different bands.
3. Multilevel Decomposition and Feature Hierarchies
DWT enables hierarchical signal analysis. At each stage, the approximation output is recursively decomposed, resulting in a tree of subband signals mapping onto specific frequency intervals:
- For a -level DWT, the transform yields and , covering spectral bands (approximation) and (detail) for sampled input at (Feudjio et al., 2021, Haddadi et al., 2017, Noyum et al., 2021).
For applications requiring full frequency tiling, the Wavelet Packet Transform (WPT) extends DWT by further decomposing both approximation and detail branches, producing a -way partition at depth (Tarafdar et al., 5 Apr 2025).
The multi-band outputs (e.g., for 4-level decomposition at 173.61 Hz) provide band-specific analysis which is crucial in neurophysiological and audio applications.
4. Algorithms and Hardware Implementations
Computationally, DWT may be implemented via convolution or lifting schemes. Lifting provides in-place and highly parallelizable architectures, reducing arithmetic complexity. For the CDF 9/7 wavelet used in JPEG 2000, the lifting scheme comprises four basic predict/update steps and two gain stages, parameterized by known constants (0710.4812):
| Stage | Coefficient | Equation |
|---|---|---|
| Predict | ||
| Update | ||
| etc. | , ... | as above |
Extensive hardware results show that pipelined lifting architectures on FPGAs achieve maximal throughput (up to 128 MHz vs. 15 MHz for naive designs) with a 40–60% area overhead, and with substantially reduced power at fixed frequency (0710.4812). Behavioral (HDL) designs mapped to shift-add networks are more area-efficient than structural ones, with minimal PSNR loss from fixed-point coefficient rounding.
On parallel hardware (GPUs), separable 1-/2-D DWT is dominant, but non-separable and polyconvolutional strategies halve the number of synchronization steps, delivering 10–30% throughput gains on VLIW and pixel shader architectures with bit-exact output (Barina et al., 2017).
5. Applications Across Domains
5.1. Biomedical Signal Processing
DWT is widely used for feature extraction in EEG and ECG signals. For seizure detection, raw DWT subband coefficients undergo PCA and fusion to produce vectors input to SVM, KNN, or NB classifiers, achieving up to 100% recognition rates on the Bonn dataset (Guharoy et al., 2021). In (Feudjio et al., 2021), DWT (db2/db4) with SVM or RF outperforms MFCC and captures clinically relevant EEG bands with ~99% sensitivity/specificity. In QRS detection, eight-level DWT with db4 enables band-selective prefiltering and thresholding, yielding ~98% detection sensitivity (Haddadi et al., 2017).
5.2. Audio and Speech
DWT-based features outperform MFCC in singer identification tasks, due to enhanced time-frequency localization. Using db4 basis, four-level decompositions, and statistical features per subband, DWT+SVM achieves ~84% accuracy compared to 61% with MFCC (Noyum et al., 2021).
5.3. NLP Embedding Compression
DWT enables compact, near-lossless compression of word/sentence embeddings from various models (GloVe, SBERT, RoBERTa) by recursively extracting low-pass and high-pass components, preserving semantic performance at 50–93% dimensionality reduction (Salama et al., 31 Jul 2025). DWT consistently outperforms PCA and DCT, and is particularly effective for large-scale contextual embeddings with redundant dimensions.
5.4. Deep Learning Architectures
In vision transformers and CNNs, DWT/iDWT are used for down/up-sampling, replacing pooling or strided-convolutions. For example, in image denoising, Haar DWT is lossless and invertible, enabling preservation of all spectral content through the network; this halves FLOPs and memory usage relative to strided alternatives with negligible loss in PSNR (Li et al., 2023). In semantic segmentation, fixed DWT/iDWT layers enable faithful spatial reconstruction and substantial IoU improvements, without additional learnable parameters (Ma et al., 2018).
6. Performance, Advantages, and Limitations
DWT achieves effective separation of signals into frequency bands with both time and frequency localization. Multi-resolution coefficients provide superior feature representations for nonstationary signals compared to STFT or MFCC, as demonstrated in statistical learning pipelines (Feudjio et al., 2021, Noyum et al., 2021, Haddadi et al., 2017). In hardware, pipelined and non-separable DWTs achieve maximal throughput and efficiency on FPGA and GPU, respectively (0710.4812, Barina et al., 2017). In neural models, DWT provides lossless, invertible sampling with reduced computational footprint (Li et al., 2023, Ma et al., 2018).
Principal advantages include:
- Invertibility and exact multi-band reconstruction for orthogonal and biorthogonal wavelets.
- Perfect reconstruction with compact FIR filters.
- Superior feature generation for classification in nonstationary signal domains.
- Significant hardware acceleration potential via pipelining and computation fusion.
Limitations are context-dependent:
- Sensitivity to wavelet choice: improper basis can degrade localization or fail to capture domain-specific features (Feudjio et al., 2021, Noyum et al., 2021). Some applications do not report basis selection (Guharoy et al., 2021).
- Boundary effects and related artifact potential are unaddressed in some practical applications (Guharoy et al., 2021).
- For hardware, increased pipeline depth implies significant area overhead (0710.4812).
- Adaptivity and robustness to signal anomalies may require advanced multi-band fusion or adaptive thresholding (Haddadi et al., 2017).
7. Emerging Trends and Implementation Resources
Recent DWT toolkits, such as TFDWT, offer differentiable, end-to-end trainable DWT and IDWT operators as TensorFlow/Keras layers, supporting batchwise multi-level transforms and integration into deep learning workflows for 1D, 2D, and 3D data (Tarafdar et al., 5 Apr 2025). TFDWT supports orthogonal and biorthogonal wavelets, multi-level and wavelet-packet decompositions, and is parametrized via standard filter registries.
Advances also include DWT-based context-pyramids in CNNs (Ma et al., 2018), dual-stream feature extraction with DWT-informed resolution reduction in transformers (Li et al., 2023), and comprehensive analytic techniques leveraging DWT for data and model compression at scale in NLP and CV (Salama et al., 31 Jul 2025).
In summary, the discrete wavelet transform constitutes an essential tool for hierarchical, invertible, and efficient joint time-frequency analysis, with wide-ranging applications in signal processing, machine learning, NLP, and hardware acceleration. Recent developments continue to expand the applicability of DWT, leveraging its multi-resolution, computational, and structural properties in both model design and feature engineering.