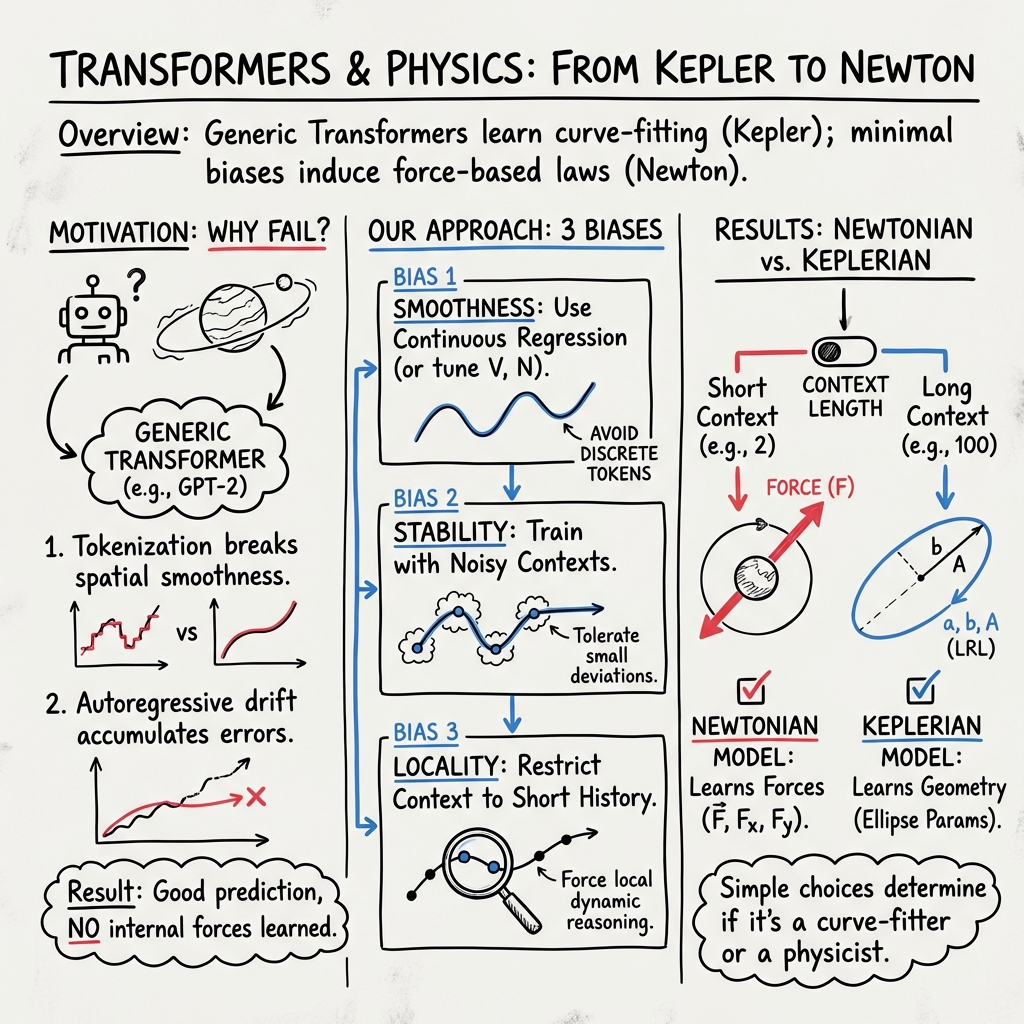
From Kepler to Newton: Inductive Biases Guide Learned World Models in Transformers

Abstract: Can general-purpose AI architectures go beyond prediction to discover the physical laws governing the universe? True intelligence relies on "world models" -- causal abstractions that allow an agent to not only predict future states but understand the underlying governing dynamics. While previous "AI Physicist" approaches have successfully recovered such laws, they typically rely on strong, domain-specific priors that effectively "bake in" the physics. Conversely, Vafa et al. recently showed that generic Transformers fail to acquire these world models, achieving high predictive accuracy without capturing the underlying physical laws. We bridge this gap by systematically introducing three minimal inductive biases. We show that ensuring spatial smoothness (by formulating prediction as continuous regression) and stability (by training with noisy contexts to mitigate error accumulation) enables generic Transformers to surpass prior failures and learn a coherent Keplerian world model, successfully fitting ellipses to planetary trajectories. However, true physical insight requires a third bias: temporal locality. By restricting the attention window to the immediate past -- imposing the simple assumption that future states depend only on the local state rather than a complex history -- we force the model to abandon curve-fitting and discover Newtonian force representations. Our results demonstrate that simple architectural choices determine whether an AI becomes a curve-fitter or a physicist, marking a critical step toward automated scientific discovery.

• The paper demonstrates that imposing minimal inductive biases—spatial smoothness, stability, and temporal locality—guides Transformers to internalize true Newtonian dynamics.
• It reveals that robust regression enhanced with noisy context outperforms discrete token classification in accurately predicting force components.
• The study identifies context length as a bifurcation parameter, transitioning model behavior from Keplerian curve-fitting to mechanistic Newtonian modeling.

Inductive Biases and the Emergence of Physical World Models in Transformers

Problem Setting and Motivation

This paper investigates whether general-purpose Transformer architectures, typically used in language modeling and sequence modeling, can learn not only to predict, but to internalize physical world models analogous to classical mechanics, specifically the Newtonian laws governing planetary motion. The core question is whether high predictive accuracy equates to a mechanistic internalization of underlying physical laws, or whether models learn only to fit observed trajectories without true physical understanding.

Previous work demonstrates that with strong, domain-specific priors ("AI Physicist" models), neural networks can recover interpretable physical laws, but generic Transformers trained at scale (as in Vafa et al., 2025) fail to encode Newtonian dynamics, even with predictive success. This work aims to identify and systematically inject minimal inductive biases necessary for Transformers to learn true world models—differentiating curve-fitting (Keplerian) from force-based (Newtonian) representations—and aims to clarify the architectural and training conditions under which genuine mechanistic understanding can, in principle, emerge.

Systematic Analysis of Failure Modes and Inductive Biases

Spatial Smoothness

Tokenization of spatial coordinates, a standard practice for adapting sequence models to spatial phenomena, introduces problems for spatial smoothness. Transforming continuous coordinates $(x, y)$ into separate tokens irreparably disrupts the geometric structure: the initial random embedding assignment causes even nearby spatial points to be maximally distant in representational space, and even exhaustive large-scale training is insufficient for the emergence of high-fidelity, linearly decodable spatial maps in the embedding space. Empirically, the coefficient of determination $R^2$ for the best-possible linear map from embeddings to true space saturates at around $0.86$—a partial recovery but insufficient for accurate force computations, which require accurate distance calculations.

The emergence of a high-quality spatial map is shown to be dictated jointly by the vocabulary size (number of bins), data coverage, and embedding dimensionality. A sharp scaling law is found: reducing vocabulary size greatly aids spatial map emergence, while further increasing embedding size rapidly yields diminishing returns. However, small vocabulary sizes necessarily reduce spatial resolution, so there is an intrinsic trade-off between smoothness and representational accuracy.

An alternative—operating directly on continuous coordinates as model inputs (regression)—circumvents the need for embedding a spatial map, but introduces new difficulties.

Spatial Stability and Robust Regression

Regressive modeling of continuous, unbounded variables is well-known to introduce instability in autoregressive generation, where errors accumulate rapidly and render predictions divergent after a few steps. Prior empirical work (Vafa et al., 2025) interprets this as regression underperforming classification, but this work demonstrates that the failure is not inherent. By introducing moderate Gaussian noise to the historical input context during training (noisy context learning), the regression model can be made significantly more robust, consistently outperforming discrete-token-based classification models in terms of mean distance error for trajectory prediction. This suggests that classification's previously observed superiority is a by-product of implicit regularization via quantization and output projection, rather than a fundamental architectural limitation.

Temporal Locality as World Model Selector

Despite robust regression capabilities and accurate next-state predictions, regression alone does not guarantee that the Transformer internalizes the Newtonian equation of motion. The crucial inductive bias is temporal locality: Newton's second law dictates that, under appropriate time sampling, the future depends only on the current and immediately preceding states.

Context length in the Transformer architecture is treated as a surrogate for temporal locality. Empirical results reveal that with large context lengths (long token histories available in the self-attention window), the model aligns with a Keplerian model, encoding geometric, global, curve-fitting parameters (ellipse axes, LRL vector, etc.) while failing to internally represent force quantities. When the context length is forcibly reduced to 2, the Transformer instead aligns with a Newtonian world model, internally representing gravitational forces ($F=ma$) with near-perfect linearity ($R^2 \approx 0.999$ for force components). Thus, context/window length acts as a bifurcation parameter controlling which world model emerges internally.

Performance-Regime Dependence and Phase Transition

A key finding is the existence of a performance-phase bifurcation controlled by context length. Large contexts facilitate improved long-horizon predictive error due to the robustness of global geometric fitting (Keplerian), albeit at the cost of true mechanistic modeling; short contexts enforce local, mechanistic (Newtonian) inference, which is more generalizable but less smooth under high inference noise. This phase transition is monotonic: as context length is interpolated, the model's internal representation smoothly transitions from geometric to mechanistic.

Practical and Theoretical Implications

The study delineates that strong predictive performance in general-purpose sequence models does not imply the discovery of mechanistic, causal world models. It demonstrates that the emergence of scientific laws inside powerful sequence architectures is highly sensitive to minimal, generic architectural and data-induced biases: spatial smoothness, spatial stability (robustness by noise injection), and—most crucially—temporal locality.

These results suggest that for generalization beyond the training regime (for example, to unseen trajectories or OOD scenarios), enforcing locality and continuity is necessary to induce mechanistic, law-based internalization, as opposed to overfitting or memorization of observed data. Therefore, "world models" must not be defined solely by predictive power, but require explicit benchmarks for mechanistic inference. Furthermore, the findings call into question the sufficiency of predictive pretraining for developing AI agents that can autonomously discover symbolic or mechanistic principles underlying high-dimensional data.

Limitations and Outlook

The experiments utilize a synthetic, highly controlled planetary motion setup. The symbolic extraction of Newtonian laws requires probing with knowledge of the correct variables; the models do not, by themselves, output symbolic equations. The generalization to high-dimensional, less controlled, or multi-scale physical phenomena, as well as the automation of symbolic law discovery via a secondary interpreter or symbolic head, remain open problems.

Future directions include extending these architectural insights to heterogeneous or real-world domains and developing end-to-end mechanisms for symbolic abstraction and OOD scientific discovery without human supervision.

Conclusion

This work systematically unpacks why generic Transformer architectures fail to internalize mechanistic world models of classical physics and demonstrates that the injection of three minimal, generic inductive biases—spatial smoothness, spatial stability, and temporal locality—determine whether such models become curve-fitters or physicists. These results serve as a critical guidepost for the future architecture and training of AI systems intended for automated scientific discovery and reinforce the foundational distinction between predictive accuracy and mechanistic understanding in intelligent systems.

Reference: "From Kepler to Newton: Inductive Biases Guide Learned World Models in Transformers" (2602.06923)